第 12 课 NCERT 解决方案 - 数学第一部分 - 第 5 章连续性和可微性 - 练习 5.5 |设置 1

将问题 1 到 10 中给出的函数对 x 进行微分。

问题1.cos x.cos2x.cos3x

解决方案：

Let us considered y = cos x.cos2x.cos3x

Now taking log on both sides, we get

log y = log(cos x.cos2x.cos3x)

log y = log(cos x) + log(cos 2x) + log (cos 3x)

Now, on differentiating w.r.t x, we get

$\frac{1}{y}.\frac{dy}{dx}=\frac{1}{\cos x}.\frac{d}{dx}\cos x+\frac{1}{\cos2x}.\frac{d}{dx}\cos2x+\frac{1}{\cos3x}.\frac{d}{dx}\cos3x$

$\frac{1}{y}.\frac{dy}{dx}=\frac{1}{\cos x}.(-\sin x)+\frac{1}{\cos 2x}(-\sin2x).\frac{d}{dx}.2x+\frac{1}{\cos3x}.(-\sin3x).\frac{d}{dx}3x$

$\frac{1}{y}.\frac{dy}{dx}=\frac{-\sin x}{\cos x}-\frac{2\sin2x}{\cos2x}-\frac{3\sin 3x}{\cos3x}$

$\frac{dy}{dx}$= -y(tan x + 2tan 2x + 3 tan 3x)

$\frac{dy}{dx}$= -(cos x. cos 2x. cos 3x)(tan x + 2tan 2x + 3tan 3x)

问题2。 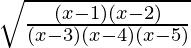$\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}$

解决方案：

Let us considered y = $\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}$

Now taking log on both sides, we get

log y = $\log (\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)})^{\frac{1}{2}}$

log y = $\frac{1}{2}$(log(x – 1)(x – 2)(x – 3)(x – 4)(x – 5))

log y = $\frac{1}{2}$(log(x – 1) + log(x – 2) – log(x – 3) – log(x – 4) – log(x – 5))

Now, on differentiating w.r.t x, we get

$\frac{1}{y}.\frac{dy}{dx}=\frac{1}{2}[(\frac{1}{x-1})+(\frac{1}{x-2})+(\frac{1}{x-3})+(\frac{1}{x-4})+(\frac{1}{x-5})]$

$\frac{dy}{dx}=\frac{y}{2}[(\frac{1}{x-1})+(\frac{1}{x-2})+(\frac{1}{x-3})+(\frac{1}{x-4})+(\frac{1}{x-5})]$

$\frac{dy}{dx}=\frac{1}{2}\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}[(\frac{1}{x-1})+(\frac{1}{x-2})-(\frac{1}{x-3})-(\frac{1}{x-4})-(\frac{1}{x-5})]$

问题 3. (log x) ^{cos x}

解决方案：

Let us considered y = (log x)^{cos x}

Now taking log on both sides, we get

log y = log((log x)^{cos x})

log y = cos x(log(log x))

Now, on differentiating w.r.t x, we get

$\frac{1}{y}.\frac{dy}{dx}=\cos x(\frac{1}{\log x}).\frac{d}{dx}\log x+\log(\log x).(-\sin x)$

$\frac{1}{y}.\frac{dy}{dx}=\frac{\cos x}{\log x}.\frac{1}{x}-\sin x \log(\log x)$

$\frac{dy}{dx}=y(\frac{\cos x}{\log x}.\frac{1}{x}-\sin x\log (\log x))$

$\frac{dy}{dx}=(\log x)^{\cos x}(\frac{\cos x}{\log x}.\frac{1}{x}-\sin x \log(\log x))$

问题 4. x ^x – 2 ^{sin x}

解决方案：

Given: y = x^x – 2^{sin x}

Let us considered y = u – v 

Where, u = x^x and v = 2^{sin x}

So, dy/dx = du/dx – dv/dx ………(1)

So first we take u = x^x

On taking log on both sides, we get

log u = log x^x      

log u = x log x    

Now, on differentiating w.r.t x, we get

$\frac{1}{u}\frac{du}{dx}=x.(\frac{1}{x})+\log x.1$

du/dx = u(1 + log x) 

du/dx = x^x(1 + log x) ………(2) 

Now we take v = 2^{sin x}

On taking log on both sides, we get

log v = log (2^sinx)

log v = sin x log2

Now, on differentiating w.r.t x, we get

$\frac{1}{v}.\frac{dv}{dx}=\log2(\cos x)$

dv/dx = v(log2cos x)

dv/dx = 2^{sin x}cos xlog2 ………(3) 

Now put all the values from eq(2) and (3) into eq(1)

dy/dx = x^x(1 + log x) – 2^{sin x}cos xlog2

问题 5. (x + 3) ² .(x + 4) ³ .(x + 5) ⁴

解决方案：

Let us considered y = (x + 3)².(x + 4)³.(x + 5)⁴

Now taking log on both sides, we get

log y = log[(x + 3)³.(x + 4)³.(x + 5)⁴]

log y = 2 log(x + 3) + 3 log(x + 4) + 4 log(x + 5)

Now, on differentiating w.r.t x, we get

$\frac{1}{y}.\frac{dy}{dx}=\frac{2}{x+3}+\frac{3}{x+4}+\frac{4}{x+5}$

$\frac{dy}{dx}=y(\frac{2}{x+3}+\frac{3}{x+4}+\frac{4}{x+5})$

$\frac{dy}{dx}=(x+3)^2(x+4)^3(x+5)^4(\frac{2}{x+3}+\frac{3}{x+4}+\frac{4}{x+5})$

问题 6。 $(x+\frac{1}{x})^x+x(1+\frac{1}{x})$

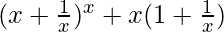
解决方案：

Given: y = $(x+\frac{1}{x})^x+x(1+\frac{1}{x})$

Let us considered y = u + v

Where $u=(x+\frac{1}{x})^x$ and $v=x^{1+\frac{1}{x}}$

so, dy/dx = du/dx + dv/dx ………(1)

Now first we take $u=(x+\frac{1}{x})^x$

On taking log on both sides, we get

log u = $\log(x+\frac{1}{x})^x$           

log u = $xlog(x+\frac{1}{x})$

Now, on differentiating w.r.t x, we get

$\frac{1}{u}.\frac{du}{dx}=x\frac{1}{(x+\frac{1}{x})}.\frac{d}{dx}(x+\frac{1}{x})+\log(x+\frac{1}{x})$

$\frac{1}{u}.\frac{du}{dx}=(\frac{x^2}{x^2+1})(\frac{x^2-1}{x^2})+\log(x+\frac{1}{x})$

$\frac{dy}{dx}=u[\frac{x^2-1}{x^2+1}+\log(x+\frac{1}{x})]$

$\frac{du}{dx}=(x+\frac{1}{x})^x(\frac{x^2-1}{x^2+1}+\log(x+\frac{1}{x}))$ ………(2)

Now we take $v=x^{1+\frac{1}{x}}$

On taking log on both sides, we get

log v = $log x^{(1 + \frac{1}{x})}$

 log v = $(1 + \frac{1}{x})log x$

Now, on differentiating w.r.t x, we get

 $\frac{1}{v}\frac{dv}{dx}=(1+\frac{1}{x})\frac{d}{dx}(\log x)\log x\frac{d}{dx}(1+\frac{1}{x})$

$\frac{dv}{dx}=v[(\frac{x+1}{x}).\frac{1}{x}+\log x(\frac{-1}{x^2})]$

$\frac{dv}{dx}=x^{1+\frac{1}{x}}.[\frac{1+1-\log x}{x^2}]$  ………(3)

Now put all the values from eq(2) and (3) into eq(1)

$\frac{dy}{dx}=(x+\frac{1}{x})^2(\frac{x^2-1}{x^2+1}+\log(x+\frac{1}{x}))+x^{(1+\frac{1}{x}).[\frac{x+1-\log x}{x^2}]}$

问题 7. (log x) ^x + x ^{log x}

解决方案：

Given: y = (log x)^x + x ^{log x}

Let us considered y = u + v

Where u = (log x)^x and v = x^{log x}

so, dy/dx = du/dx + dv/dx ………(1)

Now first we take u = (log x)^x

On taking log on both sides, we get

log u = log(log x)^x                 

log u = x log(log x)

Now, on differentiating w.r.t x, we get

$\frac{1}{u}\frac{du}{dx}=x.\frac{d}{dx}\log(\log x)+\log(\log x).\frac{d}{dx}.x$ 

$\frac{1}{u}\frac{du}{dx}=u(\frac{x}{\log x}.\frac{1}{x}+\log(\log x))$

$\frac{du}{dx}=(\log x)^x(\frac{1}{\log x}+\log(\log x))$  ………(2)

Now we take v = x^{log x}

On taking log on both sides, we get

log v = log(x^{log x})

log v = logx log(x)

log v = logx²

Now, on differentiating w.r.t x, we get

$\frac{1}{v}.\frac{dv}{dx}=\frac{d}{dx}(\log^2x)$

$\frac{1}{v}.\frac{dv}{dx}=2\log x\frac{d}{dx}(\log x)$

$\frac{dv}{dx}=v.(2\log x.\frac{1}{x})$

$\frac{dv}{dx}=x^{\log x}.\frac{2\log x }{x}$   ………(3)

Now put all the values from eq(2) and (3) into eq(1)

$\frac{dy}{dx}=(\log x)^x(\frac{1}{\log x}+\log(\log x))+x^{\log x}.\frac{2\log x}{x}$

问题 8. (sin x) ^x + sin ^–1 √x

解决方案：

Given: y = (sin x)^x + sin^–1√x

Let us considered y = u + v

Where u = (sin x)^x and v = sin^–1√x

so, dy/dx = du/dx + dv/dx ………(1)

Now first we take u = (sin x)^x

On taking log on both sides, we get

log u = log(sin x)^x

log u = xlog(sin x)

Now, on differentiating w.r.t x, we get

$\frac{1}{u}.\frac{du}{dx}=x\frac{d}{dx}(\log(\sin x))+\log(\sin x).\frac{d}{dx}x$ 

$\frac{1}{u}.\frac{du}{dx}=x.\frac{1}{\sin x}.\frac{d}{dx}.\sin x+\log(\sin x)$

$\frac{du}{dx}=u(\frac{x\cos x}{\sin x}+\log(\sin x))$

$\frac{du}{dx}=(\sin x)^x.(x\cot x+\log(\sin x))$ ………(2)

Now we take v = sin^–1√x

On taking log on both sides, we get

log v = log sin^–1√x

Now, on differentiating w.r.t x, we get

$\frac{dv}{dx}=\frac{1}{\sqrt{1-(\sqrt{x}^2)}}.\frac{d}{dx}\sqrt{x}$

$\frac{dv}{dx}=\frac{1}{2\sqrt{x-x^2}}$ ………(3)

Now put all the values from eq(2) and (3) into eq(1)

$\frac{dy}{dx}=(\sin x)^x.(x\cot x+\log(\sin x))+\frac{1}{2\sqrt{x-x^2}}$

问题 9. x ^{sin x} + (sin x) ^{cos x}

解决方案：

Given: y = x ^{sin x} + (sin x)^{cos x}

Let us considered y = u + v

Where u = x ^{sin x} and v = (sin x)^{cos x}

so, dy/dx = du/dx + dv/dx ………(1)

Now first we take u = x ^{sin x}

On taking log on both sides, we get

log u = log x^{sin x}  

log u = sin x(log x)

Now, on differentiating w.r.t x, we get

$\frac{1}{u}.\frac{du}{dx}=\sin x\frac{d}{dx}\log x+\log x\frac{d}{dx}\sin x$ 

$\frac{du}{dx}=u.[\sin x.\frac{1}{x}+\log x(\cos x)]$

$\frac{du}{dx}=x^{\sin x}(\frac{\sin x}{x}+\log x(\cos x))$ ………(2)

Now we take v =(sin x)^{cos x}

On taking log on both sides, we get

log v = log(sin x)^{cos x}

log v = cosx log(sinx)

Now, on differentiating w.r.t x, we get

$\frac{1}{v}\frac{dv}{dx}=\cos x\frac{d}{dx}\log(\sin x)+\log(\sin x).\frac{d}{dx}\cos x$

$\frac{1}{v}\frac{dv}{dx}=(\cos x.\frac{1}{\sin x}.\frac{d}{dx}\sin x+\log(\sin x).(-\sin x))$

$\frac{dv}{dx}=\sin x^{\cos x}(\cot x.\cos x-\sin x\log(\sin x))$ ………(3)

Now put all the values from eq(2) and (3) into eq(1)

$\frac{dy}{dx}=x^{\sin x}(\frac{\sin x}{x}+\log X(\cos x)+\sin x^{\cos x}(\cot x\cos x-\sin x\log(\sin x)))$

问题 10。 $x^{x\cos x}+\frac{x^2+1}{x^2-1}$

解决方案：

Given: y = $x^{x\cos x}+\frac{x^2+1}{x^2-1}$

Let us considered y = u + v

Where u = x^xcosx and v = $\frac{x^2+1}{x^2-1}$

so, dy/dx = du/dx + dv/dx ………(1)

Now first we take u = x^xcosx

On taking log on both sides, we get

log u = log (x ^xcosx)   

log u = x.cosx.logx 

Now, on differentiating w.r.t x, we get

$\frac{1}{u}\frac{du}{dx}=\frac{d}{dx}(x).cosx.logx+x.\frac{d}{dx}(cosx).logx+x.cosx.\frac{d}{dx}(logx)$

$\frac{du}{dx}=u[1.cosx.logx+x.(-sinx).logx+x.cosx.\frac{1}{x}]$

$\frac{du}{dx}=x^{xcosx}[cosx(1+logx)-xsinxlogx]$ ………(2)

Now we take v =$\frac{x^2+1}{x^2-1}$

On taking log on both sides, we get

log v = log$\frac{x^2+1}{x^2-1}$

log v = log(x² + 1) – log(x² – 1)

Now, on differentiating w.r.t x, we get

$\frac{1}{v}\frac{dv}{dx}=\frac{1}{x^2+1}.\frac{d}{dx}(x^2+1)-\frac{1}{x^2-1}.\frac{d}{dx}(x^2-1)$

$\frac{fv}{dx}=v(\frac{2x}{x^2+1}-\frac{2x}{x^2-1})$

$\frac{dv}{dx}=\frac{(x^2+1)}{(x^2-1)}(2x).(\frac{(x^2-1)-(x^2+1)}{(x^2+1)(x^2-1)})$

$\frac{dv}{dx}=\frac{(2x)(-2)}{(x^2-1)^2}$                       

$\frac{dv}{dx}=\frac{-4x}{(x^2-1)^2}$  ………(3)

Now put all the values from eq(2) and (3) into eq(1)

$\frac{dy}{dx}=x^{xcosx}[cosx(1+logx)-xsinxlogx]-\frac{4x}{(x^2-1)^2}$

第 5 章连续性和可微性——练习 5.5 |设置 2