第 12 课 NCERT 解决方案 - 数学第一部分 - 第 2 章反三角函数 - 第 2 章杂项练习 |设置 1
问题 1. 找出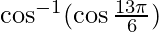
解决方案:
We know that ![]()
Here, ![]()
Now, ![]() can be written as :
can be written as :
![]() , where
, where ![]()
Hence, the value of ![]() = π/6
= π/6
问题 2. 找出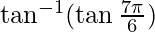
解决方案:
We know that ![]()
Here, ![]()
Now, ![]() can be written as:
can be written as:
![]()
![]() where
where ![]()
Hence, the value of ![]() = π/6
= π/6
问题 3. 证明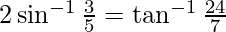
解决方案:
Let ![]() -(1)
-(1)
sin x = 3/5
So,![]() = 4/5
= 4/5
tan x = 3/4
Hence, ![]()
Now put the value of x from eq(1), we get
Now, we have
L.H.S ![]()
=  –
–![]()
![]()
Hence, proved.
问题 4. 证明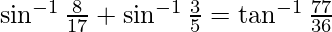
解决方案:
Let ![]()
Then sin x = 8/17
cos x = = 15/17
Therefore, ![]()
![]() -(1)
-(1)
Now, let ![]()
Then, sin y = 3/5
![]() = 4/5
= 4/5
![]() -(2)
-(2)
Now, we have:
L.H.S.![]()
From equation(1) and (2), we get
= ![]()
= 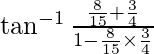
= –
![]()
= ![]()
Hence proved
问题 5. 证明![由 QuickLaTeX.com 渲染 \cos^{-1}\frac{4}{5}+\cos^{-1}\frac{12}{13}=\cos^{-1}\frac{33}{65}]()
解决方案:
Let ![]()
Then, cos x = 4/5
![]() = 3/5
= 3/5
![]()
![]() -(1)
-(1)
Now let
Then, cos y = 3/4
![]()
![]()
![]() -(2)
-(2)
Let ![]()
Then, cos z = 33/65
sin z = 56/65
![]()
![]() -(3)
-(3)
Now, we will prove that :
L.H.S. ![]()
From equation (1) and equation (2)
= ![]()
= 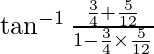 –
–![]()
= ![]()
= ![]()
Using equation(3)
= ![]()
Hence proved
问题 6. 证明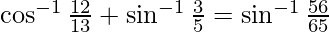
解决方案:
Let ![]()
Then, sin x = 3/5
![]() = 4/5
= 4/5
![]()
![]() -(1)
-(1)
Now, let ![]()
Then, cos y = 12/13 and sin y = 5/13
![]()
![]() -(2)
-(2)
Let ![]()
Then, sin z = 56/65 and cos z = 33/65
![]()
![]() -(3)
-(3)
Now, we have:
L.H.S.=
From equation(1) and equation(2)
=![]()
= 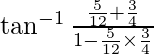 –
–![]()
= ![]()
= ![]()
From equation (3)
= ![]()
Hence proved
问题 7. 证明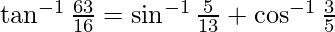
解决方案:
Let ![]()
Then, sin x = 5/13 and cos x = 12/13.
![]()
![]()
![]() -(1)
-(1)
Let ![]()
Then, cos y = 3/5 and sin y = 4/5
![]()
![]() -(2)
-(2)
From equation(1) and (2), we have
R.H.S.![]()
=![]()
= 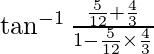 –
–![]()
=![]()
=![]()
L.H.S = R.H.S
Hence proved
问题 8. 证明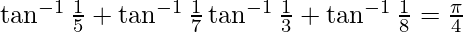
解决方案:
L.H.S.![]()
=  –
–![]()
= ![]()
= ![]()
= ![]()
= 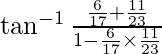
= ![]()
= ![]()
= π/4
L.H.S = R.H.S
Hence proved
问题 9. 证明![由 QuickLaTeX.com 渲染 \tan^{-1} \sqrt x= \frac{1}{2} \cos^{-1} (\frac{1-x}{1+x}),x\in[0,1]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_2_Inverse_Trigonometric_Functions_%E2%80%93_Miscellaneous_Exercise_on_Chapter_2_%7C_Set_1_103.jpg)
解决方案:
Let x = tan2θ
Then,![]()
![]()
Now, we have
R.H.S = ![]()
L.H.S = R.H.S
Hence proved
问题 10. 证明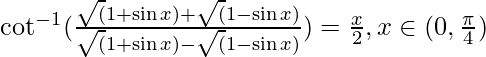
解决方案:
Consider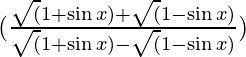
By rationalizing
=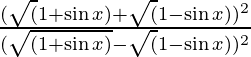
=![]()
=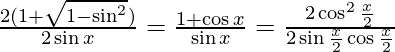
= ![]()
L.H.S = 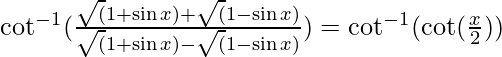 = x/2
= x/2
L.H.S = R.H.S
Hence proved