第 12 课 NCERT 解决方案 - 数学第一部分 - 导数的应用 - 练习 6.2 |设置 1

问题 1. 证明 f (x) = 3x + 17 给出的函数在 R 上是递增的。

解决方案：

If for a function f(x), f'(x) > 0 for all x, then the function is a strictly increasing function.  (vice-versa is not true)

Given: f(x) = 3x + 17

f'(x) = 3 > 0        -(Always greater than zero)

Hence, 3x + 17 is strictly increasing on R.

问题 2. 证明函数由 f (x) = e ^2x在 R 上递增。

解决方案：

If for a function f(x), f'(x) > 0 for all x, then the function is a strictly increasing function.  (vice-versa is not true)

Given: f(x) = e^2x

f’(x) = 2e^2x > 0

Hence, f(x) = e^2x is strictly increasing on ∞

问题 3. 证明 f (x) = sin x 给出的函数是

(i) 增加 (0, π/2)

(ii) 颁布 (π/2, π)

(iii) (0, π) 既不增加也不减少

解决方案：

Given: f(x) = sin x

So, f’(x) = d/dx(sin x) = cos x

(i) Now in (0, π/2), f’(x) = cos x > 0 (positive in first quadrant)

Hence, f(x) = sin x is strictly increasing in (0, π/2).

(ii) In (π/2, π), f’(x) = cos x < 0           -(negative in second quadrant)

Hence, f(x) = sin x is strictly decreasing in (π/2,π)  

(iii) As we know that f’(x) = cos x is positive in interval(0, π/2)

and f’(x) = cos x is negative in interval (π/2, π)

So, it is neither increasing nor decreasing.

问题 4. 找出 f(x) = 2x ² – 3x 给出的函数f 的区间

(一) 增加

(ii) 减少

解决方案：

Given: f(x) = 2x² – 3x

f'(x) = $\frac{d(2x^2-3x)}{dx}$ = 4x – 3           -(1)

= x = 3/4

So the intervals are (-∞, 3/4) and (3/4, ∞)

(i) Interval (3/4, ∞) let take x = 1

So, from eq(1) f'(x) > 0

Hence, f is strictly increasing in interval (3/4, ∞)

(ii) Interval (-∞, 3/4) let take x = 0.5

So, from eq(1) f'(x) < 0

Hence, f is strictly decreasing in interval (-∞, 3/4)

问题 5. 找出 f(x) = 2x ³ – 3x ² – 36x + 7 给出的函数f 的区间

(一) 增加

(ii) 减少

解决方案：

Given: f(x) = 2x³ – 3x² – 36x + 7

f'(x) = $\frac{d(2x^3-3x^2-36x+7)}{dx}$ = 6x² – 6x – 36         -(1)

f'(x) = 6(x² – x – 6)

On putting f'(x) = 0, we get

6(x² – x – 6) = 0

(x² – x – 6) = 0

x = -2, x = 3

So, the intervals are (-∞, -2), (-2, 3), and (3, ∞)

For (-∞, -2) interval, take x = -3

From eq(1), we get

f'(x) = (+)(-)(-) = (+) > 0

So, f is strictly increasing in interval (-∞, -2)

For (-2, 3) interval, take x = 2

From eq(1), we get

f'(x) = (+)(+)(-) = (-) < 0

So, f is strictly decreasing in interval (-2, 3)

For (3, ∞)interval, take x = 4

From eq(1), we get

f'(x) = (+)(+)(+) = (+) > 0

So, f is strictly increasing in interval (3, ∞)

(i) f is strictly increasing in interval (-∞, -2) and (3, ∞)

(ii) f is strictly decreasing in interval (-2, 3) 

问题 6. 找出下列函数严格递增或递减的区间：

(i) x ² + 2x – 5

(ii) 10 – 6x – 2x ²

(iii) -2x ³ – 9x ² – 12x + 1

(iv) 6 – 9x – x ²

(v) (x + 1) ³ (x – 3) ³

解决方案：

(i) f(x) = x² + 2x – 5 

f'(x) = 2x + 2         -(1)

On putting f'(x) = 0, we get

2x + 2 = 0

x = -1

So, the intervals are (-∞, -1) and (-1, ∞)

For (-∞, -1) interval take x = -2 

From eq(1), f'(x) = (-) < 0

So, f is strictly decreasing 

For (-1, ∞) interval take x = 0

From eq(1), f'(x) = (+) > 0

So, f is strictly increasing

(ii) f(x) = 10 – 6x – 2x² 

f'(x) = -6 – 4x

On putting f'(x) = 0, we get

-6 – 4x = 0

x = -3/2

So, the intervals are (-∞, -3/2) and (-3/2, ∞)

For (-∞, -3/2) interval take x = -2 

From eq(1), f'(x) = (-)(-) = (+) > 0

So, f is strictly increasing

For (-3/2, ∞) interval take x = -1

From eq(1), f'(x) = (-)(+) = (-) < 0

So, f is strictly decreasing 

(iii) f(x) = -2x³ – 9x² – 12x + 1 

f'(x) = -6x² – 8x – 12

On putting f'(x) = 0, we get

-6x² – 8x – 12 = 0

-6(x + 1)(x + 2) = 0

x = -1, x = -2

So, the intervals are (-∞, -2), (-2, -1), and (-1, ∞)

For (-∞, -2) interval take x = -3 

From eq(1), f'(x) = (-)(-)(-) = (-) < 0

So, f is strictly decreasing

For (-2, -1) interval take x = -1.5

From eq(1), f'(x) = (-)(-)(+) = (+) > 0

So, f is strictly increasing

For (-1, ∞) interval take x = 0

From eq(1), f'(x) = (-)(+)(+) = (-) < 0

So, f is strictly decreasing

(iv) f(x) = 6 – 9x – x² 

f'(x) = -9 – 2x

On putting f'(x) = 0, we get

-9 – 2x = 0

x = -9/2

So, the intervals are (-∞, -9/2) and (-9/2, ∞)

For f to be strictly increasing, f'(x) > 0

– 9 – 2x > 0

x > -9/2

So f is strictly increasing in interval (-∞, -9/2)

For f to be strictly decreasing, f'(x) < 0

-9 – 2x < 0

x < -9/2

So f is strictly decreasing in interval (-9/2, ∞)

(v) f(x) = (x + 1)³ (x – 3)³

f'(x) = (x + 3)³.3(x – 3)³ + (x – 3)³.3(x + 1)²

f'(x) = 6(x – 3)²(x + 1)²(x – 1)

Now, the factor of (x – 3)² and (x + 1)² are non-negative for all x

For f to be strictly increasing, f'(x) > 0

(x – 1) > 0

x > 1

So, f is strictly increasing in interval (1, ∞)

For f to be strictly decreasing, f'(x) < 0

(x – 1) < 0

x < 1

So, f is strictly decreasing in interval (-∞, 1)

问题 7. 证明 y = log(1 + x) – $\frac{2x}{2+x}$ , 是 x 在其整个域中的递增函数。

解决方案：

f(x) = log(1+x)$\frac{-2x}{2+x}, x>-1$

$\frac{dy}{dx}=f'(x)=\frac{1}{1+x}-\frac{(2x+1).2-2x(1)}{(2x+1)^2}$        

f'(x)=$\frac{1}{1+x}-\frac{4+2x-2x}{(2x+1)^2}$

$f'(x)=\frac{1}{1+x}-\frac{4}{(2+x)^2}$

$f'(x)=\frac{(x+2)^2-4(x+1)}{(x+1)(x+2)}$

$f'(x)=\frac{x^2}{(x+1)(x+2)^2}$

So, the domain of the given function is x > -1

Now, x² > 0, (x + 2)² ≥ 0, x + 1 > 0

From the above equation f'(x) ≥ 0 ∀ x in the domain(x > -1) and f is an increasing function.

问题 8. 找出 y = [x(x-2)] ²是递增函数的 x 的值。

解决方案：

Given: y = f(x) = [x(x – 2)]² = x²(x – 2x)²

= x⁴ – 4x³ + 4x²

f'(x) = 4x³ – 12x² + 8x

f'(x) = 4x(x – 2)(x – 1)

x = 0, x = 1, x = 2

So, (∞, 0], [0, 1], [1, 2], [2,∞)

For (∞, 0], let x = -1

So, f'(x) = (-)(-)(-) = (-) ≤ 0

f(x) is decreasing

For [0, 1], let x = 1/2

So, f'(x) = (+)(-)(-) = (+) ≥ 0

f(x) is increasing

Similarly, for [1, 2], f(x) is decreasing

For [2,∞), f(x) is increasing

So, f(x) is increasing in interval [0, 1] and [2,∞)

问题 9. 证明 y = 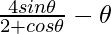$\frac{4sin\theta}{2+cos\theta}-\theta$是 θ in[0, π/2] 的增函数。

解决方案：

y = f(θ) = $\frac{4\sinθ}{(2+\cosθ)^2}-θ$

$f'(θ)=\frac{(2+\cosθ).4\cosθ-4\sinθ(-\sinθ)}{(2+\cosθ)^2}$     

$f'(θ)=\frac{4.(2\cosθ+\cos^2θ+\sin^2θ)}{(2+\cosθ)^2}-1$

$f'(θ)=\frac{8\cosθ+4}{(\cosθ+2)^2}$

$f'(θ)=\frac{8\cosθ+4-(2+\cosθ)^2}{(2+\cosθ)^2}$

$f'(θ)=\frac{4\cosθ-\cos^2θ}{(2+\cosθ)^2}$

Now 0 ≤ θ ≤ π/2, and we have 0 ≤ cosθ ≤ 1, 

So, 4 – cosθ > 0

Therefore f'(θ) ≥ 0 for 0 ≤ θ ≤ π/2

Hence, f'(x) = $\frac{4\sinθ}{2+\cosθ}-θ$ is a strictly increasing in the interval (θ, π/2).

问题 10. 证明对数函数在 (0, ∞) 上递增。

解决方案：

Given: f(x) = log(x)         -(logarithmic function)

f'(x) = 1/x ∀ x in (0, ∞) 

Therefore,  x > 0, so, 1/x > 0

Hence, the logarithmic function is strictly increasing in interval (0, ∞) 

第 6 章导数的应用——练习 6.2 |设置 2