第 12 课 NCERT 解决方案 - 数学第一部分 - 第 3 章矩阵 - 练习 3.2 |设置 2
第 3 章矩阵 - 练习 3.2 |设置 1
问题 11. 如果![由 QuickLaTeX.com 渲染 x\left[\begin{array}{l} 2 \\ 3 \end{array}\right]+y\left[\begin{array}{c} -1 \\ 1 \end{array}\right]=\left[\begin{array}{l} 10 \\ 5 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_0.jpg) ,求 x 和 y 的值。
,求 x 和 y 的值。
解决方案:
Given: ![Rendered by QuickLaTeX.com x\left[\begin{array}{l} 2 \\ 3 \end{array}\right]+y\left[\begin{array}{c} -1 \\ 1 \end{array}\right]=\left[\begin{array}{c} 10 \\ 5 \end{array}\right] \\ \Rightarrow\left[\begin{array}{c} 2 x \\ 3 x \end{array}\right]+\left[\begin{array}{c} -y \\ y \end{array}\right]=\left[\begin{array}{c} 10 \\ 5 \end{array}\right] \\ \Rightarrow\left[\begin{array}{c} 2 x-y \\ 3 x+y \end{array}\right]=\left[\begin{array}{c} 10 \\ 5 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_1.jpg)
Equating corresponding entries, we have
2x – y = 10 -(1)
3x + y = 5 -(2)
Adding eq.(1) and (2), we have 5x = 15 ⇒ x = 3
Putting x = 3 in eq.(2)
9 + y = 5 ⇒ y = -4
Therefore, x = 3 and y = -4
问题 12. 给定![由 QuickLaTeX.com 渲染 3\left[\begin{array}{cc} x & y \\ z & w \end{array}\right]=\left[\begin{array}{cc} x & 0 \\ -1 & 2 w \end{array}\right]+\left[\begin{array}{cc} 4 & x+y \\ z+w & 3 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_2.jpg) ,求 x、y、z 和 w 的值。
,求 x、y、z 和 w 的值。
解决方案:
Given: ![Rendered by QuickLaTeX.com 3\left[\begin{array}{cc} x & y \\ z & w \end{array}\right]=\left[\begin{array}{cc} x & 0 \\ -1 & 2 w \end{array}\right]+\left[\begin{array}{cc} 4 & x+y \\ z+w & 3 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_3.jpg)
![Rendered by QuickLaTeX.com \Rightarrow\left[\begin{array}{ll} 3 x & 3 y \\ 3 z & 3 w \end{array}\right]=\left[\begin{array}{cc} x+4 & 6+x+y \\ -1+z+w & 2 w+3 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_4.jpg)
Equating corresponding entries, we have
3x = x + 4 ⇒ 2x = 4 ⇒ x = 2
and 3y = 6 + x + y
⇒ 2y = 6 + 2
⇒ 2y = 8
⇒ y = 4
and 3z = -1 + z + w ⇒ 2z – w = – 1 -(1)
and 3w = 2w + 3 ⇒ w = 3
Putting w = 3 in eq(i), 2z – 3 = -1
⇒ 2z = 2 ⇒ z = 1
Therefore, x = 2, y = 4, z = 1, w = 3
问题 13. 如果![由 QuickLaTeX.com 渲染 F(x)=\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_5.jpg) ,证明 F(x) F(y) = F(x + y)。
,证明 F(x) F(y) = F(x + y)。
解决方案:
![Rendered by QuickLaTeX.com \begin{aligned} &\text { } F(x)=\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right], F(y)=\left[\begin{array}{ccc} \cos y & -\sin y & 0 \\ \sin y & \cos y & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &F(x+y)=\left[\begin{array}{ccc} \cos (x+y) & -\sin (x+y) & 0 \\ \sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &F(x) F(y)=\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos y & -\sin y & 0 \\ \sin y & \cos y & 0 \\ 0 & 0 & 1 \end{array}\right] \end{aligned}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_6.jpg)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc} \cos (x+y) & -\sin (x+y) & 0 \\ \sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_7.jpg)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc} \cos x \cos y-\sin x \sin y+0 & -\cos x \sin y-\sin x \cos y+0 & 0 \\ \sin x \cos y+\cos x \sin y+0 & -\sin x \sin y+\cos x \cos y+0 & 0 \\ 0 & 0 & 0 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_8.jpg)
= F(x + y)
= F(x) F(y) = F(x + y)
问题 14. 证明
解决方案:
(i) L.H.S =![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\\ =\left[\begin{array}{ll} 5(2)-1(3) & 5(1)-1(4) \\ 6(2)+7(3) & 6(1)+7(4) \end{array}\right]\\ =\left[\begin{array}{cc} 10-3 & 5-4 \\ 12+21 & 6+28 \end{array}\right]\\ =\left[\begin{array}{cc} 7 & 1 \\ 33 & 34 \end{array}\right] \ \ \ -(1)](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_11.jpg)
R.H.S =
Therefore, from (1) and (2), we get
![Rendered by QuickLaTeX.com \text { }\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right] \neq\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_13.jpg)
i.e. L.H.S. ≠ R.H.S
(ii) L.H.S = ![Rendered by QuickLaTeX.com \left[\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_14.jpg)
Multiply both the matrices
![Rendered by QuickLaTeX.com =\left[\begin{array}{lll} 1(-1)+2(0)+3(2) & 1(1)+2(-1)+3(3) & 1(0)+2(1)+3(4) \\ 0(-1)+1(0)+0(2) & 0(1)+1(-1)+0(3) & 0(0)+1(1)+0(4) \\ 1(-1)+1(0)+0(2) & 1(1)+1(-1)+0(3) & 1(0)+1(1)+0(4) \end{array}\right]\\ =\left[\begin{array}{ccc} 5 & 8 & 14 \\ 0 & -1 & 1 \\ -1 & 0 & 1 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_15.jpg)
R.H.S.= ![Rendered by QuickLaTeX.com \left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_16.jpg)
![Rendered by QuickLaTeX.com \begin{array}{l} =\left[\begin{array}{ccc} -1(1)+1(0)+0(1) & (-1) 2+1(1)+0(1) & (-1) 3+1(0)+0(0) \\ 0(1)+(-1) 0+1(1) & (0) 2+1(-1)+1(1) & (0) 3+0(-1)+1(0) \\ 2(1)+3(0)+4(1) & 2(2)+3(1)+4(1) & 2(3)+3(0)+4(0) \end{array}\right] \\ =\left[\begin{array}{ccc} -1 & -1 & -3 \\ 1 & 0 & 0 \\ 6 & 11 & 6 \end{array}\right] \end{array}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_17.jpg)
Therefore,
L.H.S. ≠ R.H.S.
i.e.![Rendered by QuickLaTeX.com \text { }\left[\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right] \neq\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_18.jpg)
问题 15. 求 A 2 – 5A + 6I,如果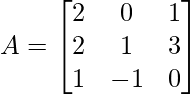
解决方案:
问题 16. 如果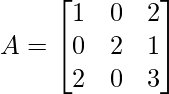 , 证明 A 3 – 6A 2 + 7A + 2I = 0
, 证明 A 3 – 6A 2 + 7A + 2I = 0
解决方案:
![Rendered by QuickLaTeX.com A=\begin{bmatrix}1&0&2\\0&2&1\\2&0&3\\\end{bmatrix} A^{2} \\=A * A=\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right]\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right] \\ =\left[\begin{array}{lll} 1+0+4 & 0+0+0 & 2+0+6 \\ 0+0+2 & 0+4+0 & 0+2+3 \\ 2+0+6 & 0+0+0 & 4+0+9 \end{array}\right] \\ =\left[\begin{array}{lll} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_24.jpg)
![Rendered by QuickLaTeX.com 6 A^{2} =6\left[\begin{array}{lll} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{array}\right]=\left[\begin{array}{ccc} 30 & 0 & 48 \\ 12 & 24 & 30 \\ 48 & 0 & 78 \end{array}\right] \\ A^{3} =A^{2} \times A \\ =\left[\begin{array}{lll} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{array}\right]\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right] \\ =\left[\begin{array}{lll} 21 & 0 & 34 \\ 12 & 8 & 23 \\ 34 & 0 & 55 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_25.jpg)
![Rendered by QuickLaTeX.com A^{3} - 6 A^{2}+7 A+2 I=\left[\begin{array}{ccc} 21 & 0 & 34 \\ 12 & 8 & 23 \\ 34 & 0 & 55 \end{array}\right]-\left[\begin{array}{ccc} 30 & 0 & 48 \\ 12 & 24 & 30 \\ 48 & 0 & 78 \end{array}\right]+\left[\begin{array}{ccc} 7 & 0 & 14 \\ 0 & 14 & 7 \\ 14 & 0 & 21 \end{array}\right]+\left[\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{array}\right]\\ =\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_26.jpg)
= 0 (Zero matrix)
= R.H.S.
Hence Proved
问题 17. 如果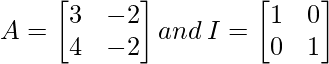 , 求 k 使得 A 2 = kA – 2I
, 求 k 使得 A 2 = kA – 2I
解决方案:
Given:
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr} 3 & -2 \\ 4 & -2 \end{array}\right] \text { and } I=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\\ A^{2}=k A-2 I \Rightarrow\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]=k\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]-2\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\\ \Rightarrow\left[\begin{array}{cc} 9-8 & -6+4 \\ 12-8 & -8+4 \end{array}\right]=\left[\begin{array}{cc} 3 k & -2 k \\ 4 k & -2 k \end{array}\right]-\left[\begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array}\right]\\ \Rightarrow\left[\begin{array}{ll} 1 & -2 \\ 4 & -4 \end{array}\right]=\left[\begin{array}{ll} 3 k-2 & -2 k-0 \\ 4 k-0 & -2 k-2 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_28.jpg)
Equating corresponding entries, we have
3k – 2 = 1
3k = 3
k = 1
and 4k = 4
k = 1
and -4 = -2k – 2
2k = 2
k = 1
Therefore, k = 1
问题 18. 如果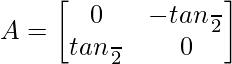 I 是 2 阶单位矩阵,证明 I + A = (I – A)
I 是 2 阶单位矩阵,证明 I + A = (I – A) 
解决方案:
![Rendered by QuickLaTeX.com \begin{array}{l} \text { L.H.S. } I+A=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]+\left[\begin{array}{cc} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{array}\right]=\left[\begin{array}{cc} 1 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 1 \end{array}\right] \\ \text { Now, } I-A=\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]-\left[\begin{array}{cc} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{array}\right]=\left[\begin{array}{cc} 1 & \tan \frac{\alpha}{2} \\ -\tan \frac{\alpha}{2} & 1 \end{array}\right] \\ \text { R.H.S. }=(I-A)\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]=\left[\begin{array}{cc} 1 & \tan \frac{\alpha}{2} \\ -\tan \frac{\alpha}{2} & 1 \end{array}\right]\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right] \end{array}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_31.jpg)
![Rendered by QuickLaTeX.com \begin{aligned} &=\left[\begin{array}{ccc} \cos \alpha+\sin \alpha \tan \frac{\alpha}{2} & -\sin \alpha+\cos \alpha \tan \frac{\alpha}{2} \\ -\cos \alpha \tan \frac{\alpha}{2}+\sin \alpha & \sin \alpha \tan \frac{\alpha}{2}+\cos \alpha \\ \end{array}\right]\\ &\text {} \end{aligned}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_32.jpg)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc} \cos \alpha \cos \frac{\alpha}{2}+\sin \alpha \sin \frac{\alpha}{2}{\cos \frac{\alpha}{2}} & \frac{\alpha \sin \alpha \cos \frac{\alpha}{2}+\cos \alpha \sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \ \\ \hline \frac{-\cos \alpha \sin \frac{\alpha}{2}+\sin \alpha \cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \frac{\sin \alpha \sin \frac{\alpha}{2}+\cos \alpha \cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_33.jpg)
![Rendered by QuickLaTeX.com \begin{aligned} &=\left[\begin{array}{cc} \frac{\cos \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} & \frac{-\sin \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} \\ \frac{\sin \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} & \frac{\cos \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} \end{array}\right]=\left[\begin{array}{ccc} \frac{\cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \frac{-\sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} \\ \frac{\sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \frac{\cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} \end{array}\right]=\left[\begin{array}{cc} 1 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 1 \end{array}\right]\end{aligned}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_34.jpg)
L.H.S. = R.H.S.
Hence, Proved.
问题 19。信托基金有 30,000 卢比,必须投资于两种不同类型的债券。第一个债券每年支付 5% 的利息,第二个债券每年支付 7% 的利息。使用矩阵乘法,确定如何在两种债券中划分 ₹30,000。如果信托基金必须获得以下年度总利息:
(a) 1800 卢比
(b) 2000 卢比
解决方案:
Let invested in the first bond = Rs x
Then, the sum of money invested in the second bond = ₹(30000 – x)
It is given that the first bond pays 5% interest per year, and the second bond pays 7% interest per year.
Thus, in order to obtain an annual total interest of ₹1800, we get:
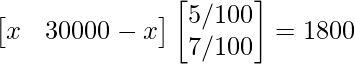
⇒ 5x/100 + 7(30000 − x)/100 = 1800
⇒ 5x + 210000 -7x = 180000
⇒ 210000 -2x = 180000
⇒ 2x = 210000 – 180000
⇒ 2x = 30000
⇒ x = 15000
Therefore, in order to obtain an annual total interest of ₹1800, the trust fund should invest ₹15000 in the first bond and the remaining ₹15000 in the second bond.
Hence, the amount invested in each type of the bonds can be represented in matrix form with each column corresponding to a different type of bond as:
X = ![]()
Hence, the interest obtained after one year can be expressed in matrix representation as:

⇒ 5x/100 + 7(30000 − x)/100 = 2000
⇒ 5x + 210000 − 7x = 200000
⇒ 210000 − 2x = 200000
⇒ 2x = 210000 – 200000
⇒ 2x = 10000
⇒ x = 5000
Therefore, in order to obtain an annual total interest of ₹2000, the trust fund should invest ₹5000 in the first bond and the remaining ₹(30000 − 5000) = ₹25000 in the second bond.
问题20。某学校的书店有10打化学书,8打物理书,10打经济学书。它们的售价分别为 80 卢比、60 卢比和 40 卢比。使用矩阵代数找出书店从出售所有书籍中将获得的总金额。
解决方案:
Let the number of books as 1 × 3 matrix = B = 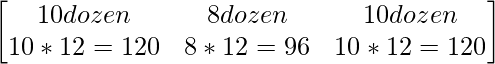
Let the selling prices of each book is a 3 × 1 matrix S = ![]()
Therefore, Total amount received by selling all books = BS = 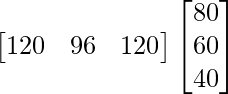
![]()
Therefore, Total amount received by selling all the books = Rs 20,160
假设 X、Y、Z、W 和 P 分别是 2 × n、3 × k、2 × p、n × 3 和 p × k 阶矩阵。在练习 21 和 22 中选择正确的答案。
问题 21. 对 n、k 和 p 的限制,以便定义 PY + WY:
(A) k = 3, p = n (B) k 是任意的, p = 2
(C) p 是任意的,k = 3 (D) k = 2,p = 3
解决方案:
Since, Matrices P and Y are of the orders p × k and 3 × k respectively.
Therefore, matrix PY will be defined if k = 3.
Then, PY will be of the order p × k = p × 3.
Matrices W and Y are of the orders n × 3 and 3 × k = 3 × 3 respectively.
As, the number of columns in W is equal to the number of rows in Y, Matrix WY is well-defined and is of the order n × 3.
Matrices PY and WY can be added only when their orders are the same.
Therefore, PY is of the order p × 3 and WY is of the order n × 3.
Thus, we must have p = n.
Therefore, k = 3 and p = n are the restrictions on n, k and p so that PY + WY will be defined.
Therefore, answer is (A)
问题 22. 如果 n = p,则矩阵 7X – 5Z 的阶数为:
(A) p × 2 (B) 2 × n
(C) n × 3 (D) p × n
解决方案:
Matrix X is of the order 2 × n.
Therefore, matrix 7X is also of the same order.
Matrix Z is of order 2 × p = 2 × n -(∵ p = n)
Then, Matrix 5Z is also of the same order.
Now, both the matrices 7X and 5Z are of the order 2 × n.
Thus, matrix 7X – 5Z is well- defined and is of the order 2 × n.
Therefore, answer is (B)
![由 QuickLaTeX.com 渲染 (i) \left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right] \neq\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_9.jpg)
![由 QuickLaTeX.com 渲染 \text { (ii) }\left[\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right] \neq\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_10.jpg)
![Rendered by QuickLaTeX.com \begin{aligned} &A^{2}-5 A+6 I=\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]-5\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]+6\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &=\left[\begin{array}{lll} 4+0+1 & 0+0-1 & 2+0+0 \\ 4+2+3 & 0+1-3 & 2+3+0 \\ 2-2+0 & 0-1-0 & 1-3+0 \end{array}\right]-\left[\begin{array}{ccc} 10 & 0 & 5 \\ 10 & 5 & 15 \\ 5 & -5 & 0 \end{array}\right]+\left[\begin{array}{lll} 6 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{array}\right] \end{aligned}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_20.jpg)
![Rendered by QuickLaTeX.com \left.\begin{array}{l} =\left[\begin{array}{ccc} 5 & -1 & 2 \\ 9 & -2 & 5 \\ 0 & -1 & -2 \end{array}\right]-\left[\begin{array}{ccc} 10 & 0 & 5 \\ 10 & 5 & 15 \\ 5 & -5 & 0 \end{array}\right]+\left[\begin{array}{ccc} 6 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{array}\right] \end{array}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_21.jpg)
![Rendered by QuickLaTeX.com \begin{array}{l} =\left[\begin{array}{ccc} 5-10+6 & -1-0+0 & 2-5+0 \\ 9-10+0 & -2-5+6 & 5-15+0 \\ 0-5+0 & -1+5+0 & -2+0+6 \end{array}\right] \\ =\left[\begin{array}{ccc} 1 & -1 & -3 \\ -1 & -1 & -10 \\ -5 & 4 & 4 \end{array}\right] \end{array}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_NCERT_Solutions-_Mathematics_Part_I_%E2%80%93_Chapter_3_Matrices_%E2%80%93_Exercise_3.2_%7C_Set_2_22.jpg)