问题1.找到三角形的质心,其顶点为:
(i)(1、4),(-1,-1)和(3,-2)
解决方案:
Given, vertices of triangle are (1, 4), (-1, -1), and (3, -2)
As we know that the coordinates of the centroid of a triangle whose vertices are (x1, y1), (x2, y2), (x3, y3)
![]()
So, the coordinates of the centroid of a triangle are![]()
= (1, 1/3)
Hence, the centroid of the triangle whose vertices are (1, 4), (-1, -1), and (3, -2) is (1, 1/3).
(i)(-2、3),(2,-1)和(4、0)
解决方案:
Given, vertices of triangle are (-2, 3), (2, -1), and (4, 0)
As we know that the coordinates of the centroid of a triangle whose vertices are (x1, y1), (x2, y2), (x3, y3)
![]()
So, the coordinates of the centroid of a triangle are![]()
= (4/3, 2/3)
Hence, the centroid of the triangle whose vertices are (-2, 3), (2, -1), and (4, 0) is (4/3, 2/3).
问题2。一个三角形的两个顶点分别是(1、2),(3、5),其质心在原点。找到第三个顶点的坐标。
解决方案:
According to question
Two vertices of a triangle are(1, 2), (3, 5), and its centroid is at the origin
Find: the coordinates of the third vertex
So, let us assume that the coordinates of the third vertex is (x, y),
So, the coordinates of the centroid of a triangle are ![]()
Ass we know that the centroid is at origin. So,
(x + 1 + 3)/3 = 0
x + 4 = 0
x = -4
(y + 2 + 5)/3 = 0
y + 7 = 0
y = -7
Hence, the third coordinate is (-4, -7)
问题3.找到三角形的第三个顶点,如果三角形的两个顶点在(-3,1)和(0,-2)且质心在原点。
解决方案:
According to the question
ABC is a triangle in which the coordinates of A are (−3, 1), B are (0, −2), and C are (a, b)
and the centroid of the triangle ABC is (0, 0)
so,
(-3 + 0 + a)/3 = 0
a = 3
(1 – 2 + b)/3 = 0
b = 1
Hence, the coordinates of third vertex is (3, 1)
问题4. A(3,2)和B(−2,1)是三角形ABC的两个顶点,其质心G具有坐标(5/3,-1/3)。找到三角形的第三个顶点C的坐标。
解决方案:
According to the question
ABC is a triangle in which the coordinates of A are (3, 2), B are (−2, 1), and C are (a, b)
and the centroid of the triangle ABC is (5/3, -1/3)
so,
(3 – 2 + a)/3 = 5/3
a = 4
(1 + 2 + b)/3 = -1/3
b = -4
Hence, the coordinates of third vertex is (4, -4)
问题5.如果(-2、3),(4,-3)和(4、5)是三角形边的中点,请找到其质心的坐标。
解决方案:

Let us assume ABC is a triangle
Now in this triangle P, Q, R be the mid point of side, AC, AB, BC.
The coordinates of P(−2, 3), Q (4, −3), and R(4, 5)
Let us assume that the coordinates of A, B, and C are (x1, y1), (x2, y2), and (x3, y3)
As we know that P is the mid point of side AC,
So,
(x1 + x3) /2 = -2
= x1 + x3 = -4 …..(1)
(y1 + y3) /2 = 3
= y1 + y3 = 6 …..(2)
As we know that Q is the mid point of side AB,
So,
(x1 + x2) /2 = 4
= x1 + x2 = 8 …..(3)
(y1 + y2) /2 = -3
= y1 + y2 = -6 …..(4)
As we know that R is the mid point of side BC,
So,
(x2 + x3) /2 = 4
= x2 + x3 = 8 …..(5)
(y2 + y3) /2 = 5
= y2 + y3 = 10 …..(6)
Now add c
2(x1 + x2 + x3) = -4 + 8 + 8 = 12 …..( 7)
x1 + x2 + x3 = 6
Now subtract eq(1), (3), (5) from eq(7), we get
x1 = 10
x2 = -2
x3 = -2
Similarly, add (2), (4), and (6), we get
2(y1 + y2 + y3) = -6 + 6 + 10 = 10
y1 + y2 + y3 = 5 ……(8)
Now subtract eq(2), (4), (6) from eq(8), we get
y1 = -1
y2 = 11
y3 = -5
so, the coordinate of ABC triangle are (10, -1), (-2, 11), and (-2, -5)
Hence, the centroid of the triangle is ((10 – 2 – 2)/3, (-1 + 11 – 5)/3) = (2, 5/3)
问题6.从分析上证明三角形两侧的中点等于第三侧的一半。
解决方案:
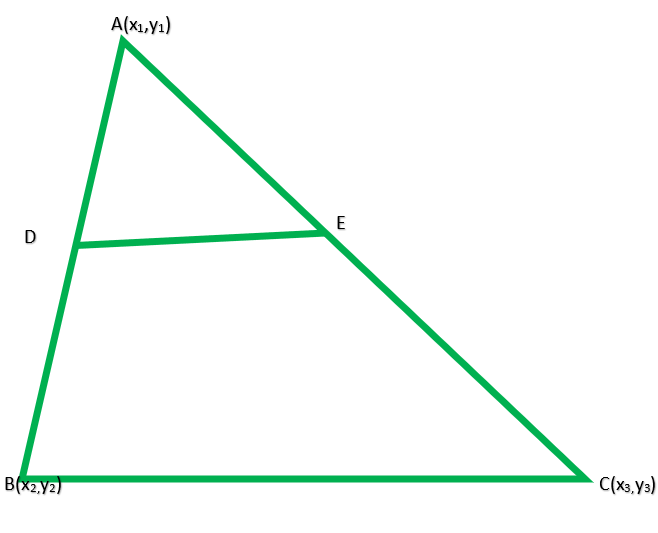
In triangle ABC,
D and E are the mid-points of the sides AB and AC
The DE = 1/2 BC
Let the coordinates of the vertices of a ∆ABC be (x1, y2), B(x2, y2), and C(x3, y3)
Then coordinates of D will be
![]()
and coordinates of E will be
![]()
Length of BC=![]() ……(1)
……(1)
and the length of DE
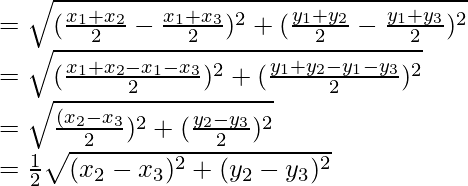
= 1/2 BC
Hence Proved
问题7:证明连接四边形相对边的中点和对角线对角点的线在一个点相交并将另一等分。
解决方案:

Let us assume the vertices of ABCD quadrilateral are A (x1, y1), B (x2, y2), C (x3, y3) and D (x4, y4)
In this quadrilateral, E and F are the mid-points of side BC and AD
and EF is joined G and H are the mid-points of diagonal AC and BD.
GH are joined
Now co-ordinates of E will be ![]()
and co-ordinates of F will be ![]()
Co-ordinates of G will be ![]()
Co-ordinates of H will be![]()
Here, EF and GH intersect each other at M.
So, let M is the midpoint of EF, then its coordinates will be
![]()
Let M is the midpoint of GH, then its coordinates of M will be
![]()
Here, we conclude that the coordinates of in both cases are same
Therefore, EF and GH bisect each other at M
问题8.如果G是三角形ABC的质心,而P是平面中的任何其他点,则证明PA 2 + PB 2 + PC 2 = GA 2 + GB 2 + GC 2 + 3GP。
解决方案:
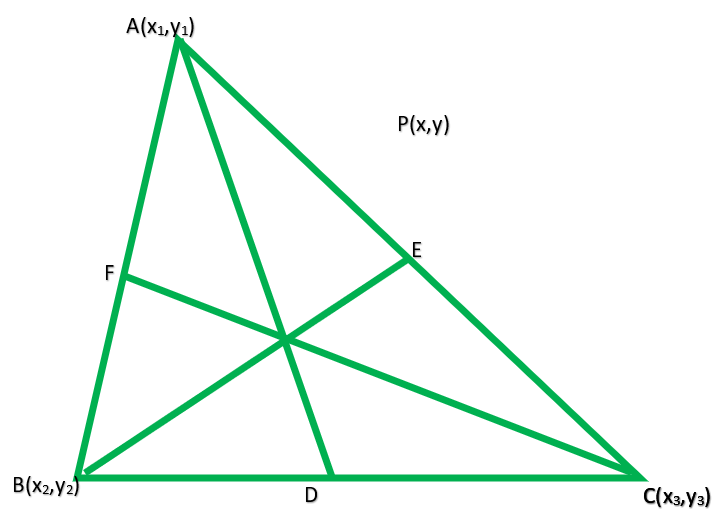
According to the question
ABC is a triangle, G is the centroid of it let P(h, x) is any point in the plane.
We have to prove that PA2 + PB2 + PC2 = GA2 + GB2 + GC2 + 3GP
Proof:
In triangle ABC,
Let us assume the coordinates of are(x1, y1) of B are(x2, y2), and of C are(x3, y3)
Therefore, co-ordinates of centroid G will be (u, v)
Where u = (x1 + x2 + 3)/3 and v = (y1 + y2 + 3)/3
Now, we shall find L.H.S and R.H.S. separately
PA2 + PB2 + PC2 = (h – x1)2 + (k – y1)2 + (h – x2)2 + (k – y2)2 + (h – x3)2 + (k – y3)2
![Rendered by QuickLaTeX.com =3(h^2+k^2)+(x^2_1+x^2_2+x_3^2)+(y_1^2+y^2_2+y_3^2)-2h(x_1+x_2+x_3)-2k(y_1+y_2+y_3)\\ =3(h^2+k^2)+(x_1^2+x_2^2+x_3^2)+(y_1^2+y_2^2+y_3^2)-2h(3u)-2k(3v)\\ =3(h^2+k^2)-6hu-6kv+(x_1^2+x_2^2+x_3^2)+(x_1^2+x_2^2+x_3^2)GA^2+GB^2+GC^2+3GD^2\\ =(u-x_1)^2+(v-y_1)^2+(u-x_2)^2+(v-y_2)^2+(u-x_3)^2+(v-y_3)^2+3[(u-h)^2+(v-k)^2]\\](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2010%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2014%20Coordinate%20Geometry%20%E2%80%93%20Exercise%2014.4_19.jpg)
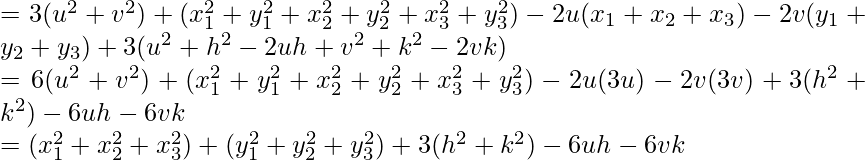
Hence proved
问题9.如果G是三角形ABC的质心,则证明AB 2 + BC 2 + CA 2 = 3(GA 2 + GB 2 + GC 2 )。
解决方案:

According to the question
ABC is a triangle and G be the centroid of this triangle
We have to prove that AB2 + BC2 + CA2 = 3(GA2 + GB2 + GC2)
Proof:
Let us assume that the coordinates of the vertices of ∆ABC be
A(x1, y1), B(x2, y2), and C(x3, y3) and let G be the centroid of the triangle
Therefore, the coordinates of G will be
![]()
Now L.H.S.= AB2 + BC2 + CA2
= (x1 – x2)2 + (y1 – y2)2 + (x2 – x3)2 + (y2 – y3)2 + (x3 – x1)2 + (y3 – y1)2
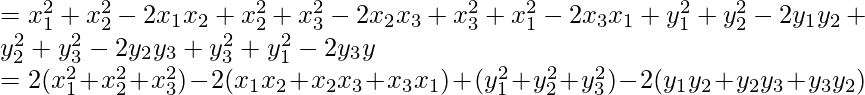
R.H.S = 3[GA2 + GB2 + GC2]
![Rendered by QuickLaTeX.com =3[(x_1-\frac{x_1+x_2+x_3}{3})^2+(y_1-\frac{y_1+y_2+y_3}{3})^2+(x_2-\frac{x_1+x_2+x_3}{3})^2+(y2-\frac{y_1+y_2+y_3}{3})^2+(x_3-\frac{x_1+x_2+x_3}{3})^3+(y_3-\frac{y_1+y_2+y_3}{3})]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2010%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2014%20Coordinate%20Geometry%20%E2%80%93%20Exercise%2014.4_24.jpg)
![Rendered by QuickLaTeX.com =3[\frac{(2x_1-x_2-x_3}{3})^2+(\frac{2y_1+y_2-y_3}{3})^2+(\frac{2x_2-x_1-x_3}{3})^2+(\frac{2y_2-y_1-y_3}{3})^2+(\frac{2y_3-x_1-x_2}{3})^2+(\frac{2y_3-y_2-y_3}{3})^2]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2010%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2014%20Coordinate%20Geometry%20%E2%80%93%20Exercise%2014.4_25.jpg)
![Rendered by QuickLaTeX.com =\frac{1}{3}[6x_1^2+6x_2^2-6x_1^2-6x_1x_2-6x_2x_3-6x_3x_1+6y_1^2+6y_2^2+6y_3^2-6y_1y_2-6y_2y_3-6y_3y_1]\\ =2[(x_1^2+x_2^2+x_3^2)-2(x_1x_2+x_2x_3+x_3x_1)+2(y_1^2+y_2^2+y_3^2+y_3^2+y_3^2)-2(y_1y_2+y_2y_3+y_3y_1)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2010%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2014%20Coordinate%20Geometry%20%E2%80%93%20Exercise%2014.4_26.jpg)
= L.H.S
Hence proved
问题10.在图中,给出了直角三角形的BOA。 C是斜边AB的中点。证明它与顶点O,A和B等距。

解决方案:
In right triangle OAB,
Co-ordinates of O are (0, 0), A are(2a, 0), and of B are(0, 2b)
C is the midpoint of AB. So, the co-ordinates of C will be
![]()
or
![]()
Now CO = ![]()
CA = 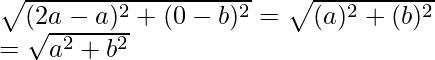
CB = 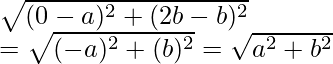
So, we can conclude that, CO = CA = CB
Hence, C is equidistant to form the vertices O, A and B.
Hence proved