第 10 类 RD Sharma 解决方案 - 第 14 章坐标几何 - 练习 14.5 |设置 1

问题 1. 求三角形的面积，其顶点为：

(i) (6, 3), (-3, 5) 和 (4, -2)

解决方案：

Let us assume ABC is a triangle whose vertices are A(6, 3), B(-3, 5) and C(4, -2)

So, 

Area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2[6(5 + 2) + (-3)(-2 – 3) + 4(3 – 5)]

= 1/2[6(5 + 2) + (-3)(-2 – 3) + 4(3 – 5)]

= 1/2[42 + 15 – 8]

= 1/2 * 49

= 49/2 sq.unit

(ii) (at ₁ ² , 2at ₁ ), (at ₂ ² , 2at ₂ ) 和 (at ₃ ² , 2at ₃ )

解决方案：

Let us assume ABC is a triangle whose vertices are A(at₁², 2at₁), (at₂², 2at₂) and (at₃², 2at₃) 

Area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2[at₁²(2at₂ – 2at₃) + at₂²(2at₃ – 2at₁) + at₃²(2at₁ – 2at₂)]

= 1/2[at₁²2at₂ – at₁²2at₃ + at₂²2at₃ – at₂²2at₁ + at₃²2at₁ – at₃²2at₂]

= 1/2 × 2a²[t₁²t₂ – t₁²t₃ + t₂²t₃ – t₂²t₁ + t₃²t₁ – t₃²t₂]

= a²[t₁²(t₂ – t₃) + t₂²(t₃ – t₁) + t₃²(t₁ – t₂)]

(iii) (a, c + a), (a, c) 和 (-a, c – a)

Let us assume ABC is a triangle whose vertices are A(a, c + a), B(a, c) and C(-a, c – a)

So, Area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2[a(c – c + a)a(c – a – c – a) + (-a)(c + a – c)]

= 1/2(a² – 2a² – a²)

= 1/2(-2a²)

= a²sq.units

问题2.求四边形的面积，其顶点坐标为

(i) (-3, 2), (5, 4), (7, -6) 和 (-5, -4)

解决方案：

Let us considered ABCD is a quadrilateral whose vertices are A(-3, 2), B(5, 4), C(7, -6) and D(-5, -4)

So, Area of ABCD = Area of ∆ABC + Area of ∆ADC   ….(1)

So, 

So, Area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2 [-3(4 + 6) + (-6 – 2) + 7(2 – 4)]

= 1/2 [-3(10) + 5 * (-8) + 7 * (-2)]

= 1/2 [-30 – 40 – 14]

= 1/2 [-30-40-14]

= 1/2 (-84)

= -42 

= 42 sq.units (Area cannot be in negative)

Similarly, area of ∆ADC

= 1/2 [-3(-6 + 4) + 7(-4 – 2) + (-5)(2 + 6)]

 = 1/2 [-3(-2) + 7(-6) + (-5)(8)]

 = 1/2 [6 – 42 – 40]

= 1/2 (-76) 

= -38

= 38 sq. Units(Area cannot be in negative)

Now put all these values in eq(1), we get

Area of quadrilateral ABCD = 42 + 38 = 80 sq.units

(ii) (1, 2), (6, 2), (5, 3) 和 (3, 4)

解决方案：

Let us considered ABCD is a quadrilateral whose vertices are A(1, 2), B(6, 2), C(5, 3) and D(3, 4)

So, Area of ABCD = Area of ∆ABC + Area of ∆ADC   ….(1)

So, Area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2 [1(2 – 3) + 6(3 – 2) + 5(2 – 2)]

= 1/2[-1 + 6 + 0]

= 1/2 (5) 

= 5/2 sq.units

Similarly, area of ∆ADC

= 1/2 [1(3 – 4) + 5(4 – 2) + 3(2 – 3)] 

= 1/2 [1 * (-1) + 5 * 2 + 3 * (-1)] 

= 1/2 [-1 + 10 – 3]

= 1/2 * 6 

= 3 sq.units

Now put all these values in eq(1), we get

Area of quadrilateral ABCD = 5/2 + 3 = (5 + 6)/2 = 11/2 sq.units 

(iii) (-4, -2), (-3, -5), (3, -2), (2, 3)

解决方案：

Let us considered ABCD is a quadrilateral whose vertices are A(-4, -2), B(-3, -5), C(3, -2), D(2, 3) 

So, Area of ABCD = Area of ∆ABC + Area of ∆ADC   ….(1)

So, Area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2 [-4(-5 + 2) – 3(-2 + 2) + 3(-2 + 5)]

 = 1/2 [-4 * (-3) – 3 * 0 + 3 * 3]

 = 1/2 [12 + 0 + 9] 

= 1/2 * 21 

= 21/2 sq.units

Similarly, area of ∆ADC,

= 1/2 [-4(-2 – 3) + 3(3 + 2) + 2(-2 + 2)] 

= 1/2[-4 * (-5) + 3 * 5 + 2 * 0]

= 1/2 [20 + 15 + 0] 

= 1/2 * 35

= 35/2 sq.units

Now put all these values in eq(1), we get

Area of quadrilateral ABCD = 21/2 + 35/2 + 56/2 = 28 sq.units

问题 3. 四边形的四个顶点依次为 (1, 2), (-5, 6), (7, -4) 和 (k, -2)。如果四边形的面积为零，求 k 的值？

解决方案：

Let us considered ABCD is a quadrilateral whose vertices are A(1, 2), B(-5, 6), C(7, -4) and D(k, -2)

So, Area of ABCD = Area of ∆ABC + Area of ∆ADC   ….(1)

Now area of ∆ABC

= 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2 [1(6 + 4) + (-5)(-4 – 2) + 7(2 – 6)]

= 1/2 [1 * 10 + (-5)(-6) + 7(-4)]

= 1/2 [10 + 30 – 28]

= 1/2 × 12 

= 6sq.units

Similarly, area of ∆ADC,

= 1/2 [1(-4 + 2) + 7(-2 – 2) + k(2 + 4)]

= 1/2 [1(-2) + 7(-4) + k(-4)]

 = 1/2 [-2 – 28 + 6k]

= 1/2 (-30 + 6k) 

= -15+3k

= 3k – 15 sq.units

Now put all these values in eq(1), we get

Area of quadrilateral ABCD = 6 + 3k – 15

But it is given that the area of quadrilateral ABCD = 0  

So, 

0 = 6 + 3k – 15

k = 9/3 = 3

Hence, the value of k is 3.

问题 4. ΔABC 的顶点分别是 (-2, 1)、(5, 4) 和 (2, -3)。通过 A 求三角形的面积和高度的长度。

解决方案：

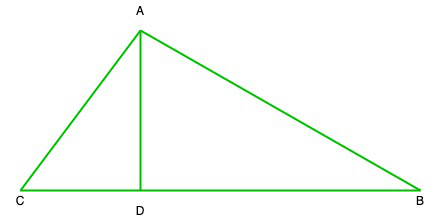
Given that, ABC is a triangle whose vertices are A(-2, 1), B(5, 4), and C(2, -3)

and AD ⊥ BC, let us assume AD = h

So, area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2 [-2(4 + 3) + 5(-3 – 1) + 2(1 – 4)]

= 1/2 [-2 * 7 + 5 * (-4) + 2(-3)]

= 1/2[-14 – 20 – 6] 

= 1/2 * (-40)

= -20

= 20 sq. units

Now we find the length of BC = 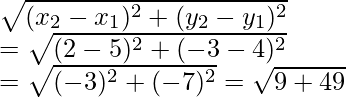$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(2-5)^2+(-3-4)^2}\\ =\sqrt{(-3)^2+(-7)^2}=\sqrt{9+49}$

= √58 units

So, the area of ∆ABC = 1/2 * base * height

⇒ 20 = 1/2 * 58 * h 

⇒ h = (20 * 2)/√58 = 40/√58 units

问题 5. 证明下列点集是共线的

(i) (2, 5), (4, 6) 和 (8, 8)

解决方案：

As we know that 3 points are collinear is the area of the triangle formed by them is zero

So, let us assume ABC is a triangle whose vertices A(2, 5), B(4, 6) and C(8, 8)

So, area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2[2(6 – 8 + 4(8 – 5) + 8(5 – 6)]

= 1/2 [2 * (-2) + 4 * 3 + 8 * (-1)]

= 1/2 [-4 + 12 – 8]

= 1/2 * 0 = 0

Area of ∆ABC = 0

Hence, points A, B and C are collinear                                 

Hence proved

(b) (1, -1), (2, 1) 和 (4, 5)

解决方案：

As we know that 3 points are collinear is the area of the triangle formed by them is zero

So, let us assume ABC is a triangle whose vertices A(1, -1), B(2, 1) and C(4, 5)

So, area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2 [1(1 – 5) + 2(5 + 1) + 4(-1 – 1)]

= 1/2 [1(-4) + 2 * 6 + 4(-2)]

= 1/2 [-4 + 12 – 8]

= 1/2 * 0 = 0

Area of ∆ABC = 0

Hence, points A, B and C are collinear                                 

Hence proved

问题 6. 求一个四边形 ABCD 的面积，其顶点坐标为 A (-3, 2), B (5, 4), C (7, -6), D (-5, -4)。

解决方案：

Given that, ABCD is a quadrilateral whose vertices A (-3, 2), B (5, 4), C (7, -6), and D (-5, -4). 

So, Area of quadrilateral ABCD = area of ∆ABC + area of ∆ACD

= 1/2|(-12 – 30 + 14) – (10 + 28 + 18)| + 1/2|(18 – 28 – 10) – (14 + 30 + 12)|

= 1/2|-28 – 56| + 1/2|-20 – 56|

= 1/2|-84| + 1/2|-76|

= 42 + 38

= 80 sq.units

Hence, the area of quadrilateral is 80 sq.units

问题 7. 在 ΔABC 中，顶点 A 的坐标是 (0, -1)，D (1, 0) 和 E (0, 1) 分别是边 AB 和 AC 的中点。如果F是C边的中点，求ΔDEF的面积。

解决方案：

Given that ∆ABC, the coordinates of vertex A are (0, -1) and D (1, 0) and E (0, 1) are

the mid points of the sides AB and AC

Let us considered B (p, q), C (r, s) and F (x, y)

So, Mid-point of AB = Coordinates of D

$(\frac{0+p}{2},\frac{-1+q}{2})=(1,0)$

p/2 = 1

p = 2

Therefore, B(p, q) = B(2, 1)

(-1 + q)/2 = 0

-1 + q = 0

q = 1

Mid-point of AC = coordinates of E

$(\frac{0+r}{2},\frac{-1+s}{2})=(0,1)$

r/2 = 0

r = 0

(-1 + s)/2 = 1

-1 + s = 2

s = 3

Now, C(r, s) = C(0, 3)

Coordinates of F = Midpoint of BC

$(x,y)=(\frac{p+r}{2},\frac{q+s}{2})\\ =(\frac{2+0}{2},\frac{1+3}{2})=F(1,2)$

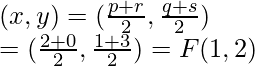
So, the coordinates of A(0,-1), B(2, 1) and C(0, 3)

Area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2 [0(1 – 3) + 2(3 + 1) + 0(-1 – 1)]

= 1/2(8) = 4sq.units

And the coordinate of D(1, 0), E(0, 1), and F(1, 2)

Area of ∆DEF = 1/2[1(1 – 2) + 0(2 – 0) + 1(0 – 1)]

= 1/2(-1 – 1) = -1

= 1 sq.unit (Area cannot be in negative)

问题 8. 求三角形 PQR 的面积与 Q (3, 2) 以及通过 Q 的边的中点为 (2, -1) 和 (1, 2)。

解决方案：

Given that, ∆PQR, L and N are mid-points of QR and QP, and the coordinates of Q are (3, 2) of L are (2, -1) and of N are (1, 2)

Let us assume that the coordinates of R be (x₁, y₁) and P(x₂,y₂)

2 = (3 + x₁)/2 ⇒ 3 + x₁ = 4 ⇒ x₁ = 4 – 3 = 1

and -1 = (2 + y)/2 ⇒ -2 = 2 + y ⇒ y = -2 – 2 = -4 

The coordinates of R are (1,-4)

Similarly coordinates of P will be 

1 = (3 + x₁)/2 ⇒ 3 + x₁ = 2 ⇒ x₁ = 2 – 3 = -1

and (2 + y)/1 = 2 ⇒ 2 + y = 4 ⇒ y = 4 – 2 = 2

Coordinates of P are (-1, 2)

Now area of ∆PQR

= 1/2 [(-12 + 2 – 2) – (2 + 4 + 6)]

= 1/2[-12 – 12] = -12

= 12 sq.units

问题 9. 如果 P (-5, -3), Q (-4, -6), R (2, -3) 和 S (1, 2) 是四边形 PQRS 的顶点，求其面积。

解决方案：

Given that, PQRS quadrilateral whose vertices are P (-5, -3), Q (-4, -6), R (2, -3) and S (1, 2) 

Area of PQRS quadrilateral = Area of ∆PQR + Area of ∆PSR   ….(1)

Now area of ∆PQR = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2[-5(-6 + 3) + (-4)(-3 + 3) + 2(-3 + 6)]

= 1/2[-5 * (-3) + (-4 * 0) + 2 * 3]

= 1/2(15 + 0 + 6)

= 1/2 * 21 

= 21/2

Similarly the area ∆PSR,

= 1/2[-5 * (2 + 3) + 1(-3 + 3) + 2(-3 – 2)]

= 1/2[-5 * 5 + 1 * 0 + 2 * (-5)]

= 1/2[-25 + 0 – 10]

= 1/2 * (-35)

= -35/2

Now put all these values in eq(1), we get

Area of quadrilateral PQRS = 21/2 + (-35/2) = 28 sq.unit

问题 10. 如果 A (-3, 5), B (-2, -7), C (1, -8) 和 D (6, 3) 是四边形 ABCD 的顶点，求其面积。

解决方案：

Let us considered ABCD is a quadrilateral whose vertices areA (-3, 5), B (-2, -7), C (1, -8), and D (6, 3)

So, Area of ABCD = Area of ∆ABC + Area of ∆ACD   ….(1)

So, Area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2 [-3(-7 + 8) + (-2)(-8 – 5) + 1(5 + 7)]

= 1/2 [-3 * 1 + 26 + 12]

= 1/2[-3 + 26 + 12]

= 35/2 sq.units

Similarly, area of ∆ACD = 1/2[-3(-8 – 3) + 1(3 – 5) + 6(5 + 8)] 

= 1/2 [-3 * (-11) + 1(-2) + 6 * 13] 

= 1/2[33 – 2 + 78]

= 1/2 * 109

= 109/2 sq.units

Now put all these values in eq(1), we get

Area of quadrilateral ABCD = 35/2 + 109/2 = 144/2 = 72 sq.units

问题 11. 对于 'a' 的值，点 (a, 1)、(1, -1) 和 (11, 4) 共线？

解决方案：

Let us assume the vertices of ∆ABC are A (a, 1), B (1, -1) and C (11, 4)

Now area of ∆ABC = 1/2[x₁(y₂ – y₃) + (y₃ – y₁)x₂ + x₃(y₁ – y₂)]

= 1/2[a(-1 – 4) + 1(4 – 1) + 11(1 + 1)]

= 1/2[-5a + 3 + 22]

= 1/2(25 – 5a)

It is given that the points A,B an C are collinear 

so, area of ∆ABC = 0

1/2 (25 – 5a) = 0  

⇒ 25 – 5a = 0

⇒ a = 25/5 = 5

Hence, the value of a is 5