第 10 类 RD Sharma 解决方案 - 第 14 章坐标几何 - 练习 14.3 |设置 1

问题 1. 求以 3:4 的比例在内部分割连接 (-1, 3) 和 (4, – 7) 的线段的点的坐标。

解决方案：

Assume P(x, y) be the needed point.

After applying the Section Formula, 

As we know that here the coordinates are

$x=\frac{mx_2+nx_1}{m+n}\\ y=\frac{my_2+ny_1}{m+n}$

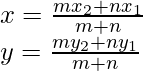
Now here we have,

x₁ = – 1 

y₁ = 3

x₂  = 4 

y₂ = -7

m : n = 3 : 4

Thus,

$x=\frac{3\times4+4\times(-1)}{3+4}\times3\\ x=\frac{3\times4+4\times(-1)}{3+4}\\ x=\frac{12-4}{7}\\ x=\frac{8}{7}\\ y=\frac{3\times(-7)+4\times3}{3+4}\\ y=\frac{-21+12}{7}\\ y=\frac{-9}{7}$

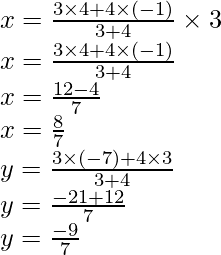
Hence, 

The coordinates of P are (8/7, -9/7)

问题 2. 求连接点的线段的三等分点：

(i) (5, – 6) 和 (-7, 5)

(ii) (3, – 2) 和 (-3, – 4)

(iii) (2, – 2) 和 (-7, 4)

解决方案：

(i) Assume P and Q are the points of trisection for AB 

Thus,

AP = PQ = QB

Thus, 

P divides AB within in the ratio of 1 : 2, 

After putting in Section Formula, 

The coordinates of P are

$\left(\frac{2(-7)+(5)}{2+1}\right),\ \left(\frac{2(5)+1(-6)}{2+1}\right)\ i.e, \ \left(1,-\frac{7}{3}\right)$ 

After this, 

Q also divides AB within in the ratio of 2 : 1. 

Hence, their coordinates are

$\left(\frac{2(-7)+1(5)}{2+1}\right),\ \left(\frac{2(5)+1(-6)}{2+1}\right)\ i.e,\ \left(-3,\ \frac{4}{3}\right)$

(ii) Assume P and Q are the points of trisection of AB i.e., AP = PQ = QB

Thus, P divides AB within in the ratio of 1 : 2. 

Therefore, after putting in the Section Formula, 

The coordinates of P are

$\left(\left(\frac{1(-3)+2(3)}{1+2}\right),\ \frac{1(-4)+(-2)}{1+2}\right)\ i.e.,\ \left(1,\ -\frac{8}{3}\right)$

After this, 

Q also divides as within in the ratio of 2 : 1

Thus, the coordinates of Q are shown as

$\left(\left(\frac{1(-3)+2(3)}{1+2}\right),\frac{1(-4)+(-2)}{1+2}\right)\ i.e.,\ \left(-1,\ \frac{-10}{3}\right)$

(iii) Assume P and Q are the points of the trisection of AB  

i.e., AP = PQ = OQ

As, P divides AB within in the ratio 1 : 2. 

Thus, the coordinates of P, by putting in the Section Formula, are shown as

$\left(\left(\frac{1(-7)+2(2)}{1+2}\right),\left(\frac{1(4)+2(-2)}{1+2}\right)\right),\ i.e.,\ \left(-1,\ 0\right)$

After this, 

Q also divides AB putting in the ration 2 : 1.

Thus, the coordinates of Q are shown as

$\left(\frac{2(-7)+1(2)}{2+1},\ \frac{2(4)+1(2)}{2+1}\right)\ i.e.,\ (-4,\ 2)$

问题 3. 求 (-2, -1)、(1, 0)、(4, 3) 和 (1, 2) 点连接形成的平行四边形的对角线相交点的坐标。

解决方案：

Assume: A(-2, -1), B(1, 0), C(4, 3) and D(1, 2) are the given points.

Assume P(x, y) is the point of intersection of the diagonals of the 

parallelogram as formed by the given points. as shown in the fig.

As we know that, the diagonals of a parallelogram bisect each other.

$x=\frac{-2+4}{2}\\ x=\frac{2}{2}=1\\ y=\frac{-1+3}{2}=\frac{2}{2}=1$

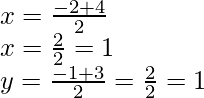
Hence,

The coordinates of P are (1, 1).

问题 4. 证明点 (3, 2), (4, 0), (6, -3) 和 (5, -5) 是平行四边形的顶点。

解决方案：

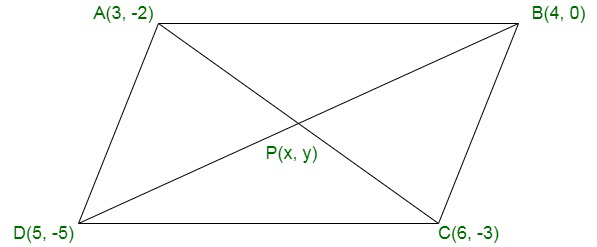
Assume: A(3, -2), B(4, 0), C(6, -3) and D(5, -5)

Assume P(x, y) is the point of intersection of diagonals AC and BD of ABCD. As shown in the fig.

Now, the mid-point of AC is shown as,

$x=\frac{3+6}{2}=\frac{9}{2}\\ y=\frac{-2-3}{2}=\frac{-5}{2}$

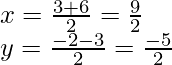
Mid – point of AC $\left(\frac{9}{5},\ \frac{-5}{2}\right)$

Now again, the mid-point of BD is shown as,

$x=\frac{5+4}{2}=\frac{9}{2}\\ y=\frac{-5+0}{2}=\frac{-5}{2}$

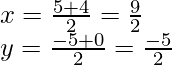
Thus, suppose that diagonals AC and BD bisect each other.

Also, as we know that diagonals of a parallelogram bisect each other.

Hence, 

ABCD is a parallelogram.

问题 5. 如果 P(9a – 2, -b) 将连接 A(3a + 1, -3) 和 B(8a, 5) 的线段以 3 : 1 的比例分割，求 a 和 b 的值。

解决方案：

Given: P(9a – 2, -b) divides the line segment joining A(3a + 1, -3) and B(8a, 5) in the ratio 3 : 1

After applying Section Formula

Coordinates of P are

$9a-2=\frac{3(8a)+1(3a+1)}{3+1}$

And,

$-b=\frac{3(5)+1(-3)}{3+1}$

Now, lets solve for a, we will have

(9a – 2) × 4 = 24a + 3a + 1

36a – 8 = 27a + 1

9a = 9

a = 1

Now, lets solve for b, we will have

4x – b = 15 – 3

-4b = 12

b = -3

Hence, 

The values of a and b are 1 and -3 respectively.

问题 6. 如果 (a, b) 是连接点 A (10, -6)、B(k, 4) 和 a – 2b = 18 的线段的中点，求 k 的值和距离 AB。

解决方案：

Given: (a, b) is the mid-point of the line segment A(10, -6) and B(k, 4)

Thus,

(a, b) = $\left(\frac{10 + k } {2}, \frac{-6 + 4}{ 2}\right)$

a = $\frac{(10 + k)}{ 2}$ and b = -1

2a = 10 + k

k = 2a – 10

Given, a – 2b = 18

Apply b = -1 above we will get,

a – 2(-1) = 18

a = 18 – 2 = 16

Since,

k = 2(16) – 10 = 32 – 10 = 22

Therefore,

AB = $\sqrt{(22 - 10)^2 + (4 + 6)^2} = \sqrt{(12)^2 + (10)^2} = \sqrt{144 + 100}$= 2√61 units

问题 7. 求点 (2, y) 与连接点 A(-2, 2) 和 B(3, 7) 的线段的比值。另外，求 y 的值。

解决方案：

Assume: Point P(2, y) divide the line segment joining the points A(-2, 2) and B(3, 7) in the ratio k : 1

Thus, the coordinates of P will be given by

$\left[\frac{3k+(-2)\times1}{k+1},\ \frac{7k+2\times1}{k+1}\right]\\ =\left[\frac{3k-2}{k+1},\ \frac{7k+2}{k+1}\right]$

Also, given the coordinates of P are (2, y)

So,

$2 = \frac{(3k - 2)}{ (k + 1)}\ and\ y = \frac{(7k + 2)}{ (k + 1)}$

Thus, solving for k, we will get

2(k + 1) = (3k – 2)

2k + 2 = 3k – 2

k = 4

Now use the value of k to find y, 

we have

y = 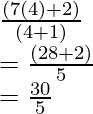$\frac{(7(4) + 2)}{ (4 + 1)}\\ = \frac{(28 + 2)}{5}\\ = \frac{30}{5}$

y = 6

Hence, 

The ratio 4 : 1 and y = 6

问题 8. 如果 A(-1, 3), B(1, -1) 和 C(5, 1) 是三角形 ABC 的顶点，求中线通过 A 的长度。

解决方案：

Assume AD is the median through A.

Such that, AD is the median, D is the mid-point of BC

Thus, 

The coordinates of D $\left(\frac{1 + 5}{ 2},\ \frac{-1 + 1}{ 2 }\right)$ are  = (3 , 0)

Therefore,

The length of median AD = $\sqrt{(3 + 1)^2 + (0 - 3)^2} =\sqrt{(4)^2 + (-3)^2} = \sqrt{16 + 9} = \sqrt{25}$ = 5 units

问题 9. 如果点 P, Q(x, 7), R, S(6, y) 依次将连接 A(2, p) 和 B (7, 10) 的线段分成 5 等份，求x、y 和 p。

解决方案：

Given: AP = PQ = QR = RS = SB

Since, 

Q is the mid-point of A and S

Then,

$x = \frac{2 + 6}{ 2} = \frac{8}{2} = 4\\ 7 = \frac{y + p}{ 2}$

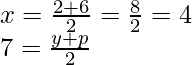
y + p = 14 ….. (i)

Thus,  

Since S divides QB in the ratio 2 : 1

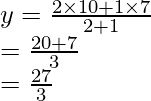$y=\frac{2\times10+1\times7}{2+1}\\ =\frac{20+7}{3}\\ =\frac{27}{3}$ = 9

Therefore, 

p = 14 – 9 = 5

Hence, 

x = 4, 

y = 9 

and 

p = 5

问题 10. 如果三角形的一个顶点是 (1, 1) 并且通过它的边的中点是 (-2, 3) 和 (5, 2) 找到其他顶点。

解决方案：

Assume, A(1, 1) is the given vertex and 

D(-2, 3), E(5, 2) be the mid-points of AB and AC

So, D and E are the mid-points of AB and AC

$\frac{x_1+1}{2}=-2,\ \frac{y_1+1}{2}=3$

 x₁ + 1 = 4

x₁ = -5

y₁ + 1 = 6

y₁  = 5

Thus, the coordinates of B are (-5, 5)

Now,

$\frac{x_2+1}{2}=5,\ \frac{y_2+1}{2}=2$

x₂ + 1 = 10

x₂ = 9

y₂ + 1 = 4

y₂ = 3

Hence,  

The coordinates of C are (9, 3)

Hence, 

The other vertices of the triangle are (-5, 5) and (9, 3).

问题 11 (i)。连接点 (-2, -3) 和 (3, 7) 的线段除以 y 轴的比例是多少？另外，求分割点的坐标。

解决方案：

Assume P(-2, -3) and Q(9, 3) be the given points.

Assume y-axis divides PQ in the ratio k : 1 at R(0, y)

Thus, the coordinates of R are shown by

$\left(\frac{3k+(-2)\times1}{k+1},\frac{7k+(-3)\times1}{k+1}\right)$

After, equating

$\frac{3k+(-2)\times1}{k+1}$

= 0

3k – 2 = 0

k = 2/3

Hence, 

The ratio is 2 : 3

After putting k = 2/3 in the coordinates of R, we will get

R (0, 1)

问题 11 (ii)。连接 (-3, -1) 和 (-8, -9) 的线段在点 (-5, -21/5) 处的分割比例是多少？

解决方案：

Assume A(-3, -1) and B(-8, -9) are the given points.

And, 

Assume P be the point that will divide AB in the ratio of k : 1

Thus, the coordinates of P can be shown by

$\left(\frac{-8k-3}{k+1},\ \frac{-9k-1}{k+1}\right)$

Therefore, given coordinates of P

After equating, we will get

$\frac{-8k - 3}{ k + 1} = -5$

-8k – 3 = -5k – 5

3k = 2

k = 2/3 

Hence, the point P divides AB in the ratio 2 : 3

问题 12. 如果连接 (3, 4) 和 (k, 7) 的线的中点是 (x, y) 并且 2x + 2y + 1 = 0 求 k 的值。

解决方案：

Since, (x, y) is the mid-point

x = (3 + k)/2 and y = (4 + 7)/2 = 11/2

Given: Mid-point lies on the line 2x + 2y + 1 = 0

$2\times\frac{(3 + k)}{ 2} + 2\times\frac{11}{2} + 1 = 0$

3 + k + 11 + 1 = 0

Therefore, 

k = -15

问题 13. 求点 P(3/4, 5/12) 分割连接点 A(1/2, 3/2) 和 B(2, -5) 的线段的比率。

解决方案：

Given: Points A($\frac{1}{2},\ \frac{3}{2}$) and B(2, -5)

Assume the point P($\frac{3}{4},\ \frac{5}{12}$) and divide the line segment AB into the ratio of k : 1

Thus, as we know that

$P\left(\frac{3}{4},\ \frac{5}{12}\right) = \frac{2k + \frac{1}{2}}{k +1} ,\ \frac{2k + \frac{3}{2}}{k + 1}$

Hence, we will equate the abscissa we will get;

$\frac{3}{4} = \frac{2k + \frac{1}{2}}{ k +1}$

3(k + 1) = 4(2k + 1/2)

3k + 3 = 8k + 2

5k = 1

k = 1/5 

Hence, 

The point P($\frac{3}{4},\ \frac{5}{12}$) divides in ratio of 1 : 5.

问题 14. 求连接 (-2, -3) 和 (5, 6) 的线除以的比率

(i) x 轴

(ii) y 轴

此外，在每种情况下找到分割点的坐标。

解决方案：

Assume A(-2, -3) and B(5, 6) are the given points.

(i) Assume x-axis divides AB in the ratio of k : 1 at the point P.

Hence, the coordinates of the point of division are shown as,

$\left[\frac{5k-2}{k+1},\ \frac{6k-3}{k+1}\right]$

Thus, P lies in the x-axis, 

The y – coordinate is zero.

Therefore,

$\frac{6k - 3}{ k + 1} = 0$

6k – 3 = 0

k = 1/2  

Therefore, 

Required ratio is 1 : 2

Applying value of k in the coordinates of P

We will get, P $(\frac{1}{3},\ 0)$

(ii) Assume y-axis divides AB in the ratio of k : 1 at the point Q.

Hence, the coordinates of the point of division are shown as,

$\left[\frac{5k-2}{k+1},\ \frac{6k-3}{k+1}\right]$

Thus, Q lies on the y-axis, 

The x – ordinate is zero.

Therefore,

$\frac{5k - 2}{ k + 1} = 0\\ 5k - 2 = 0\\ k = \frac{2}{5}$

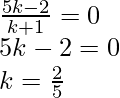
Therefore, 

Required ratio is 2 : 5

Applying the value k in the coordinates of Q

We will get, Q $(0, \frac{-3}{7})$

问题 15. 证明点 (4, 5), (7, 6), (6, 3), (3, 2) 是平行四边形的顶点。是长方形吗？

解决方案：

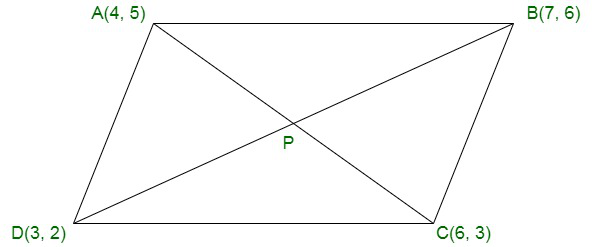
Assume A (4, 5), B(7, 6), C(6, 3) and D(3, 2) are the given points, as shown in the fig

And, 

Let the point P be the point of intersection of AC and BD.

Mid-point of AC coordinates are $\left(\frac{4+6}{2} ,\ \frac{5+3}{2}\right)$ = (5, 4)

Mid-point of BD coordinates are $\left(\frac{7+3}{2} ,\ \frac{6+2}{2}\right)$ = (5, 4)

Therefore, we can see that the mid-point of AC and BD are same.

Hence, 

ABCD is a parallelogram.

Now,

AC = $\sqrt{(6 - 4)^2 + (3 - 5)^2} = \sqrt{(2)^2 + (-2)^2} = \sqrt{4 + 4}$= √8 units

and,

BD = $\sqrt{(7 - 3)^2 + (6 - 2)^2} = \sqrt{(4)^2 + (4)^2} = \sqrt{16 + 16}$ = √32 units

Therefore,  

AC ≠ BD

Hence, ABCD is not a rectangle.

问题 16. 证明 (4, 3), (6, 4), (5, 6) 和 (3, 5) 是正方形的角点。

解决方案：

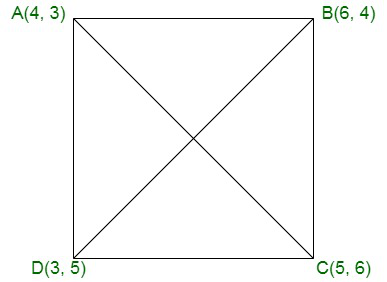
Assume A(4, 3), B(6, 4), C(5, 6), and D(3, 5) are the given points, as shown in the figure.

By applying Distance Formula:

$d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\\ AB=\sqrt{(4-6)^2+(3-4)^2}=\sqrt5\\ BC=\sqrt{(6-5)^2+(4-6)^2}\\ CD=\sqrt{(5-3)^2+(6-5)^2}\\ AD=\sqrt{(4-3)^2+(3-5)^2}$

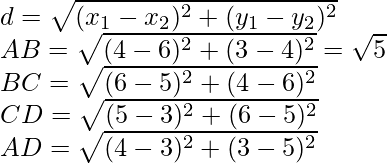
We can see that the length of all the sides are same.

Now,

The length of diagonals are;

$AC=\sqrt{(4-5)^2+(3-6)^2}=\sqrt{10}\\ BD=\sqrt{(6-3)^2+(4-5)^2}=\sqrt{10}$

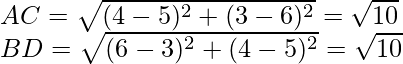
The length of both the diagonals are same.

Hence, we can say that the given points are the angular points of a square.

问题 17. 证明点 (-4, -1), (-2, -4), (4, 0) 和 (2, 3) 是矩形的顶点。

解决方案：

Assume A(-4, -1), B(-2, -4), C(4, 0) and D(2, 3) are the given points.

Now,

Mid-point of AC coordinates are $(-4 + \frac{4}{ 2},\ -1 + \frac{0}{2}) = (0,\ \frac{-1}{2})$

Mid-point of BD coordinates are $(-2 + \frac{2}{2},\ -4 + \frac{3}{2}) = (0,\ \frac{-1}{2})$

Hence, 

We can see that AC and BD have the same point.

And, 

Now for the diagonals

$AC=\sqrt{(4+4)^2+(0+1)^2}=\sqrt{65}\\ BD=\sqrt{(-2-2)^2+(-4-3)^2)}=\sqrt{65}$

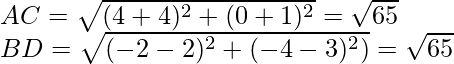
Thus length of diagonals are also same.

Hence, the given points are the vertices of a rectangle.

问题 18. 求顶点为 A(-1, 3)、B(1, -1) 和 C(5, 1) 的三角形的中线长度。

解决方案：

Assume AD, BF and CE are the medians of ΔABC

Coordinates of D are $(5 + \frac{1}{ 2},\ 1\ -\ \frac{1}{ 2})$ = (3, 0)

Coordinates of E are $(-1 + \frac{1}{ 2},\ 3\ -\ \frac{1}{ 2})$ = (0, 1)

Coordinates of F are $(5\ -\ \frac{1}{ 2},\ 1 + \frac{3}{ 2})$ = (2, 2)

Now,

Obtaining the length of the respectively medians:

Length of AD = $\sqrt{(-1-3)^2+(3+0)^2}$ = 5 units

Length of BF = $\sqrt{(2-1)^2+(2+1)^2}$ = 10 units

Length of CE = $\sqrt{(5-0)^2+(1-1)^2}$ = 5 units

问题 19. 求连接点 A (3, -3) 和 B (-2, 7) 的线段除以 x 轴的比率。另外，求分割点的坐标。

解决方案：

Assume the point on the x-axis be (x, 0).  {y – coordinate is zero}

And, 

Allow this point to divide the line segment AB in the ratio of k : 1.

After applying the Section Formula for the y-coordinate, 

we will get

$0 = \frac{7k - 3}{k + 1}$

7k – 3 = 0

k = 3/7 

Hence, x – axis divides the line segment AB in the ratio of 3 : 7.

问题 20. 求点 P(x, 2) 与连接点 A (12, 5) 和 B (4, -3) 的线段的比值。另外，求 x 的值。

解决方案：

Assume P divide the line joining A and B 

and 

Allow it to divide the segment in the ratio of k : 1

After applying the Section Formula for the y – coordinate 

we will get

$2 = \frac{-3k + 5}{k + 1}$

2(k + 1) = -3k + 5

2k + 2 = -3k + 5

5k = 3

k = 3/5 

Therefore, 

The line segment AB is divided by P in the ratio of 3 : 5

By applying the value of k, 

We will get the x – coordinate as

x = 12 + 60/8 = 72/8 = 9

Hence, the coordinates of point P is (9, 2).