10类NCERT解决方案-第7章坐标几何-练习7.2

问题1.找到以(2：3)将(–1、7)和(4，–3)的连接相除的点的坐标。

解决方案：

Let the point P (x,y) divides the line AB in the ratio 2:3

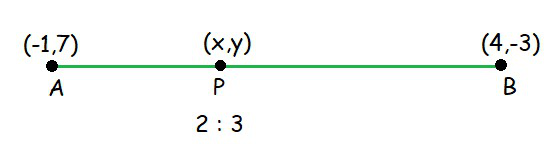
where,

m = 2 and n = 3

x₁ = -1 and y₁ = 7

x₂ = 4 and y₂ = -3

so, the x coordinate of P will be,

x = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x = $\frac{2*4 + 3*(-1)}{ 2+3}$

x = $\frac{5}{5}$

x = 1

and now, the y coordinate of P will be,

y = $\mathbf{\frac{my_2 + ny_1}{m+n}}$

y = $\frac{(2*(-3) + 3*7)}{2+3}$

y = $\frac{15}{5}$

y = 3

Hence, the coordinate of P(x,y) is (1,3)

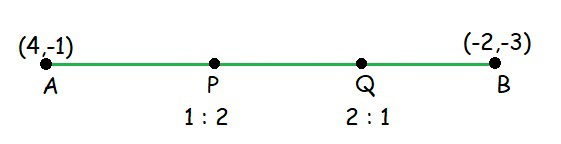
问题2。找到连接(4，–1)和(–2，–3)的线段的三等分点的坐标。

解决方案：

Let the point P (x₁,y₁) and Q(x₂,y₂) trisects the line.

So, we can conclude that

P divides the line AB in the ratio 1:2.

and Q divides the line AB in the ratio 2:1.

• For P

m = 1 and n = 2

x₁ = 4 and y₁ =-1

x₂ = -2 and y₂ = -3

so, the x coordinate of P will be,

x = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x = $\frac{(1*(-2) + 2*4)}{1+2}$

x = 2

and now, the y coordinate of P will be,

y = $\mathbf{\frac{my_2 + ny_1}{m+n}}$

y = $\frac{(1*(-3) + 2*(-1))}{ 1+2}$

y =$\frac{-5}{3}$

Hence, the coordinate of P is (2,$\mathbf{\frac{-5}{3}}$).

• For Q

m = 2 and n = 1

x₁ = 4 and y₁ =-1

x₂ = -2 and y₂ = -3

so, the x coordinate of Q will be,

x = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x = $\frac{(2*(-2) + 1*4)}{2+1}$

x = 0

and now, the y coordinate of Q will be,

y = $\mathbf{\frac{my_2 + ny_1}{m+n}}$

y = $\frac{(2*(-3) + 1*(-1)}{ 2+1}$

y = $\frac{-7}{3}$

Hence, the coordinate of Q is (0,$\mathbf{\frac{-7}{3}}$).

问题3.为进行运动日活动，在长方形的校园ABCD中，用粉笔粉在每条1m的距离处绘制了线条。如图7.12所示，沿AD彼此相距1m放置了100个花盆。 Niharika运行四分之一^日的距离AD上的第二线和支柱绿色旗帜。普里特运行1/5^个的距离AD上第八行和帖子红旗。两个标志之间的距离是多少?如果Rashmi必须在连接两个标志的线段中间恰好发布一个蓝色标志，那么她应该在哪里发布她的标志?

解决方案：

As the given data,

AD = 100 m

Preet posted red flag at $\frac{1}{5}$ of the distance AD

= ($\frac{1}{5}$ ×100) m

= 20m from the starting point of 8th line.

Therefore, the coordinates of this point will be (8, 20).

Similarly, Niharika posted the green flag at $\frac{1}{4}$th of the distance AD

= ($\frac{1}{4}$ ×100) m

= 25m from the starting point of 2nd line.

Therefore, the coordinates of this point will be (2, 25).

Distance between these flags can be calculated by using distance formula,

Distance between two points having coordinates (x₁,y₁) and (x₂,y₂) = √((x₁-x₂)² + (y₁-y₂)²)

Distance between these flags = √((8-2)² + (20-25)²)

= √(6² + 5²)

Distance between these flags = √61 m

Now as, Rashmi has to post a blue flag exactly halfway between the two flags. Hence, she will post the blue flag in the mid- point of the line joining these points. where,

m = n =1

(x₁,y₁) = (8, 20)

(x₂,y₂) = (2, 25)

x = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x = $\frac{(1*2 + 1*8)}{1+1}$

x = $\frac{10}{2}$

x = 5

and now, the y coordinate of Q will be,

y = $\mathbf{\frac{my_2 + ny_1}{m+n}}$

y = $\frac{(1*25 + 1*20)}{1+1}$

y = $\frac{45}{2}$

y = 22.5

Hence, Rashmi should post her blue flag at 22.5m on 5th line.

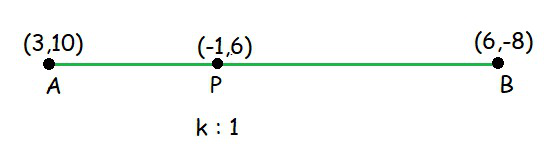
问题4。求将连接点(– 3，10)和(6，– 8)的线段除以(– 1，6)的比率。

解决方案：

Lets consider the ratio in which the line segment joining (-3, 10) and (6, -8) is divided by point (-1, 6) be k :1.

m = k and n =1

(x₁,y₁) = (3, 10) and (x2,y2) = (6,-8)

x = -1

x =$\mathbf{\frac{mx_2 + nx_1}{m+n}}$

-1 = $\frac{(k*6 + 1*3)}{k+1}$

-1(k+1) = 6k+3

k = $\mathbf{\frac{2}{7}}$

Hence, the required ratio is 2:7.

问题5.找到连接A(1，– 5)和B(– 4，4，5)的线段除以x轴的比率。还找到分割点的坐标。

解决方案：

Let the point P divides the line segment joining A (1, – 5) and B (– 4, 5) in the ratio m : 1.

Therefore, the coordinates of the point of division, say P(x, y) and,

We know that y-coordinate of any point on x-axis is 0.

P(x, 0)

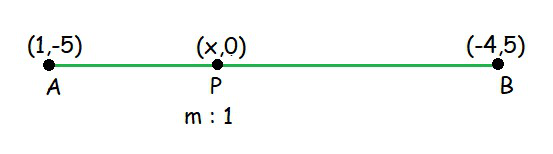
m = m and n = 1

(x₁,y₁) = (1, -5)

(x₂,y₂) = (-4,5)

so, as the y coordinate of P is 0,

y =$\mathbf{\frac{my_2 + ny_1}{m+n}}$

0 = $\frac{(m*5 + 1*(-5))}{m+1}$

5m-5=0

m = 1

So, x-axis divides the line segment in the ratio 1:1.

and, x = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x = $\frac{(1*(-4) + 1*1)}{1+1}$

x = $\frac{-3}{2}$

Hence, the coordinate of P is ($\mathbf{\frac{-3}{2}}$,0).

问题6.如果(1、2)，(4，y)，(x，6)和(3、5)是按顺序获取的平行四边形的顶点，则求出x和y。

解决方案：

Let P, Q, R and S be the points of a parallelogram : P(1,2), Q(4,y), R(x,6) and S(3,5).

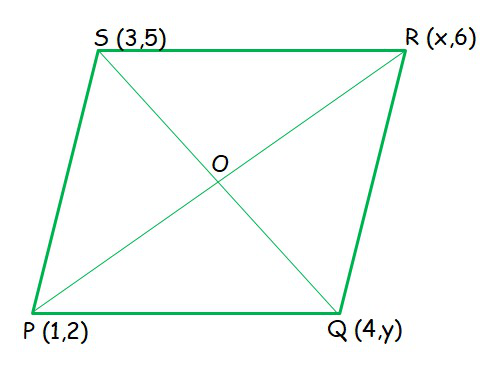
Mid point of PR = Mid point of QS (The diagonals of a parallelogram bisect each other, the midpoint O is same)

• Mid point of PR

m = 1 and n = 1

(x₁,y₁) = (1, 2)

(x₂,y₂) = (x,6)

so, the x coordinate of O will be,

x_o = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x_o = $\frac{(1*x) + 1*1)}{1+1}$

x_o = $\frac{(x+1)}{2}$

and now, the y coordinate of O will be,

y_o = $\mathbf{\frac{my_2 + ny_1}{m+n}}$

y_o = $\frac{(1*6 + 1*2)}{ 1+1}$

y_o = 4

So, the coordinate of O is ($\mathbf{\frac{(x+1)}{2}}$ , 4) ……………..(1)

• For mid point QS

m = 1 and n = 1

(x₁,y₁) = (3,5)

(x₂,y₂) = (4,y)

so, the x coordinate of O will be,

x_o = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x_o = $\frac{(1*4) + 3*1)}{1+1}$

x_o = $\frac{7}{2}$

and now, the y coordinate of O will be,

y_o = $\mathbf{\frac{my_2 + ny_1}{m+n}}$

y_o = $\frac{(1*y + 1*5)}{1+1}$

y_o = $\frac{(5+y)}{2}$

also , the coordinate of O is $(\mathbf{\frac{7}{2},\frac{(5+y)}{2}})$……………..(2)

From (1) and (2)

$\frac{(1+x)}{2} = \frac{7}{2}$ and 4 = $\frac{(5+y)}{2}$

x = 6 and y = 3

问题7.找到点A的坐标，其中AB是圆的直径，其圆心为(2，– 3)，B为(1，4)。

解决方案：

Let the coordinates of point A be (x, y).

Mid-point of AB is C(2, – 3), which is the centre of the circle.

and, Coordinate of B = (1, 4)

For mid point of two points (x₁,y₁) and (x₂,y₂)

x = $\mathbf{\frac{x_2 + x_1}{2}}$

y = $\mathbf{\frac{y_2 + y_1}{2}}$

By using this formula, we get

(2, -3) = $\frac{(x+1)}{2}$, $\frac{(y+4)}{2}$

$\frac{(x+1)}{2}$ = 2 and $\frac{(y+4)}{2}$ = -3

x + 1 = 4 and y + 4 = -6

x = 3 and y = -10

The coordinates of A (3,-10).

问题8.如果A和B分别为(– 2，– 2)和(2，– 4)，则找到P的坐标，使得AP = 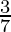$\frac{3}{7}$ AB和P位于线段AB上。

解决方案：

The coordinates of point A and B are (-2,-2) and (2,-4) respectively. Since AP = $\mathbf{\frac{3}{7}}$ AB

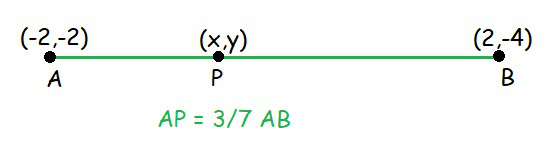
$\frac{AB}{AP}$ = $\frac{7}{3}$——–(1)

subtract 1 from both sides,

$\frac{AB}{AP}$ – 1 = $\frac{7}{3}$ – 1

$\frac{AB-AP}{AP} = \frac{7-3}{3}$

$\frac{BP}{AP} = \frac{4}{3}$

Therefore, AP: PB = 3:4

Point P divides the line segment AB in the ratio 3:4.

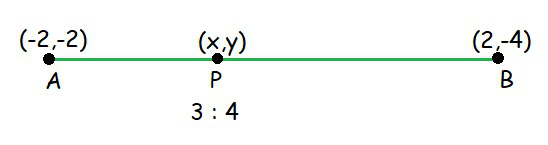
Here,

m = 3 and n = 4

(x₁,y₁) = (-2,-2)

(x₂,y₂) = (2,-4)

so, the x coordinate of P will be,

x = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x = $\frac{(3*2 + 4*(-2))}{3+4}$

x = $\frac{-2}{7}$

and now, the y coordinate of P will be,

y = $\mathbf{\frac{my_2 + ny_1}{m+n}}$

y = $\frac{(3*(-4) + 4*(-2))}{ 3+4}$

y = \frac{-20}{7}

Hence, the coordinate of P(x,y) is $(\mathbf{\frac{-2}{7}} , \mathbf{\frac{-20}{7}})$.

问题9.找到将连接A(– 2，2)和B(2，8)的线段分成四个相等部分的点的坐标。

解决方案：

Line segment joining A(– 2, 2) and B(2, 8) divided into four equal parts.

• We can say that Q is the mid point of AB

Here,

m = 1 and n = 1

(x₁,y₁) = (-2,2)

(x₂,y₂) = (2,8)

so, the x coordinate of Q will be,

x = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x = $\frac{(1*2 + 1*(-2))}{ 1+1}$

x = 0

and now, the y coordinate of Q will be,

y = \mathbf{\frac{my_2 + ny_1}{m+n}}

y = $\frac{(1*8 + 1*2)}{ 1+1}$

y = 5

Hence, the coordinate of Q is (0,5)……………………………..(1)

• We can say that P is the mid point of AQ

Here,

m = 1 and n = 1

(x₁,y₁) = (-2,2)

(x₂,y₂) = (0,5)

so, the x coordinate of P will be,

x = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x = $\frac{(1*0 + 1*(-2))}{ 1+1}$

x = -1

and now, the y coordinate of P will be,

y = $\mathbf{\frac{my_2 + ny_1}{m+n}}$

y = $\frac{(1*5 + 1*2)}{1+1}$

y = $\frac{7}{2}$

Hence, the coordinate of P is (-1,$\mathbf{\frac{7}{2}}$)……………………………..(2)

• Now, we can say that R is the mid point of BQ

Here,

m = 1 and n = 1

(x₁,y₁) = (2,8)

(x₂,y₂) = (0,5)

so, the x coordinate of R will be,

x = $\mathbf{\frac{mx_2 + nx_1}{m+n}}$

x = $\frac{(1*0 + 1*2)}{1+1}$

x = 1

and now, the y coordinate of R will be,

y = $\mathbf{\frac{my_2 + ny_1}{m+n}}$

y = $\frac{(1*5 + 1*8)}{ 1+1}$

y = $\frac{13}{2}$

Hence, the coordinate of R is (1,$\mathbf{\frac{13}{2}}$)……………………………..(3)

From (1), (2) and (3) we conclude that

Three points between A and B are (-1,$\mathbf{\frac{7}{2}}$), (0,5) and (1,$\mathbf{\frac{13}{2}}$).

问题10.如果菱形的顶点依次是(3，0)，(4，5)，(– 1，4)和(– 2，– 1)，则求出菱形的面积。[提示：菱形的面积=½(对角线的乘积)]

解决方案：

Let P(3, 0), Q (4, 5), R(– 1, 4) and S (– 2, – 1) are the vertices of a rhombus PQRS.

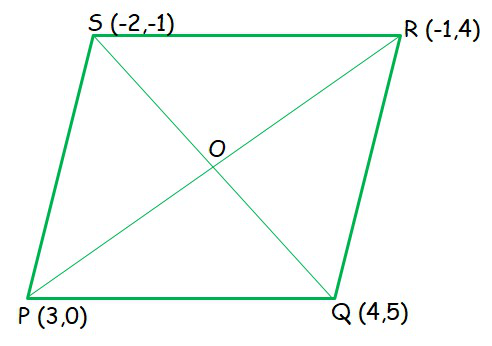
Area of a rhombus = ½ (product of its diagonals)

Length of diagonal 1 (PR) = √((3-(-1))²+(0-4)²) = √32 = 4√2 units

Length of diagonal 2 (QS) = √((4-(-2))²+(5-(-1))²) = √72 = 6√2 units

Area of a rhombus = ½ × 4√2 × 6√2

Area of a rhombus = 24 sq. units