问题11:如果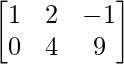 + A =
+ A = 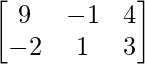 。
。
解决方案:
Given,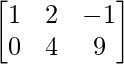 + A =
+ A =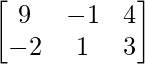 .
.
=> A =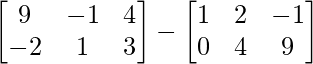
=> A =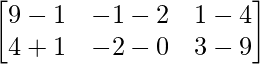
=> A =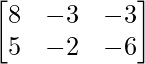
问题12:如果A = 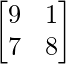 ,B =
,B =  ,找到C,使5A + 3B + 2C为空矩阵。
,找到C,使5A + 3B + 2C为空矩阵。
解决方案:
Given 5A + 3B + 2C =O, where O is the null matrix.
=> 2C = O – 5A – 3B.
=> 5A =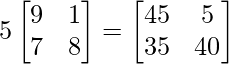
=> 3B =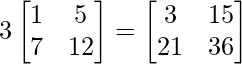
=> 2C =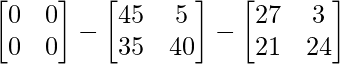
=> 2C =
=> 2C =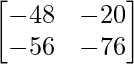
=> C =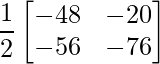
=> C =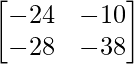
问题13:如果A = 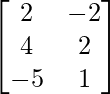 ,B =
,B =  ,找到矩阵X,使2A + 3X = 5B。
,找到矩阵X,使2A + 3X = 5B。
解决方案:
Given 2A + 3X = 5B.
=> 3X = 5B – 2A.
=> 5B =
=> 2A =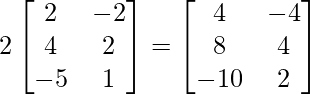
=> 3X =
=> 3X =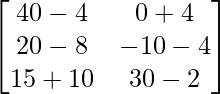
=> 3X =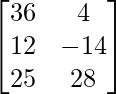
=> X =
=> X =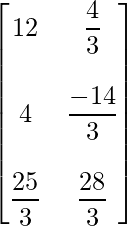
问题14:如果A = 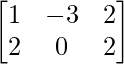 和B =
和B = 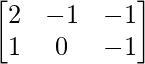 ,找到矩阵C,使得A + B + C为零矩阵。
,找到矩阵C,使得A + B + C为零矩阵。
解决方案:
Given that A + B + C = O, where O is a null matrix.
=> C = O – A – B.
=> C =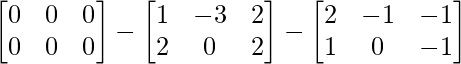
=> C =
=> C =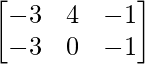
问题15(i):找出满足矩阵方程的x,y 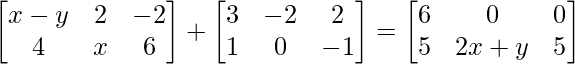
解决方案:
Given that,
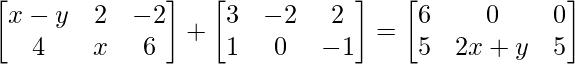
We can arrive at 2 equations from the above matrix equation.
=> x – y + 3 = 6
=> x – y = 3 ……(eq.1)
=> x + 0 = 2x + y
=> -x = y ……….(eq.2)
Solving (eq.1) and (eq.2) for x and y.
=> 2x = 3
=> x = 3/2
Substitute x in (eq.2)
=> y = -3/2
问题15(ii):找出满足矩阵方程的x,y和z 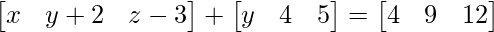
解决方案:
Given that,
![]()
=>![]()
=>![]()
We can arrive at 3 equations from the above matrix equation.
=> x + y = 4 ……(eq.1)
=> y + 6 = 9 ……(eq.2)
=> z + 2 = 12 ….(eq.3)
From (eq.2),
=> y = 9 – 6
=> y = 3
From (eq.3),
=> z = 12 – 2
=> z = 10
Substitute the value of y in (eq.1),
=> x + 3 = 4
=> x = 4 – 3
=> x = 1
问题15(iii):找出满足矩阵方程的x和y 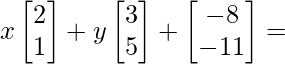 哦
哦
解决方案:
Given that,
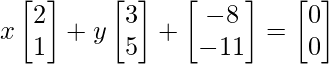
We can arrive at 2 equations from the above matrix equation.
=> 2x + 3y – 8 = 0
=> 2x + 3y = 8 …….(eq.1)
=> x + 5y -11 = 0
=> x + 5y = 11 …….(eq.2)
Solving for x and y , (eq.1) – 2.(eq.2),
=> 2x -2x + 3y – 10y = 8 – 22
=> -7y = -14
=> y = 2
Substitute y in (eq.2),
=> x + 5(2) = 11
=> x = 11 – 10
=> x = 1
问题16:如果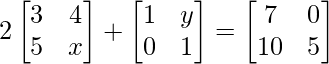 ,找到x和y。
,找到x和y。
解决方案:
Given that,
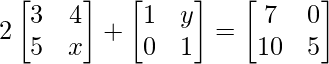
We can arrive at 2 equations from the above matrix equation.
=> 2x + 1 = 5…….(eq.1)
=> 8 + y = 0……..(eq.2)
Solving for x,
=> 2x = 5 – 1
=> 2x = 4
=> x = 2
Solving for y,
=> y = -8
问题17:找到的价值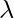 ,非零标量,如果
,非零标量,如果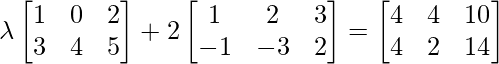
解决方案:
Given that,
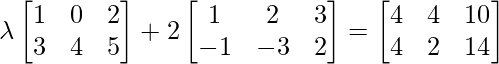
=> We can arrive at several equations to solve for![]() however lets take one.
however lets take one.
=>![]()
=>![]()
If we substitute![]() , in the matrix we see that the equation remains consistent.
, in the matrix we see that the equation remains consistent.
Hence,![]() .
.
问题18(i):找出一个矩阵X使得2A + B + X = O,其中A = 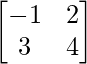 ,B =
,B =  。
。
解决方案:
Given that, 2A + B + X = O.
=> 2A =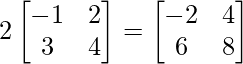
=> X = O – 2A – B
=> X =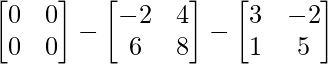
=> X =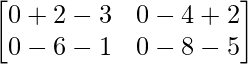
=> X =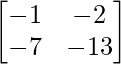
问题18(ii):如果A =  和B =
和B = 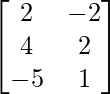 ,然后找到3×2阶的矩阵X,使得2A + 3X = 5B。
,然后找到3×2阶的矩阵X,使得2A + 3X = 5B。
解决方案:
Given that 2A + 3X = 5B.
=> 3X = 5B – 2A.
=> 5B =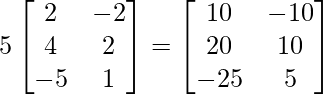
=> 2A =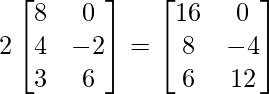
=> 3X =
=> 3X =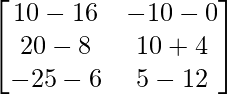
=> 3X =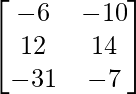
=> X =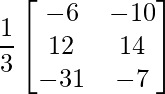
=> X =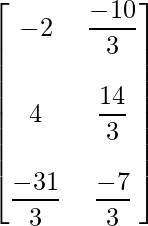
问题19(i):找出x,y,z和t 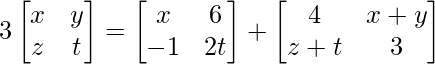 。
。
解决方案:
Given that,

We can arrive at 4 different equations from the above matrix equation,
=> 3x = x + 4 …………(eq.1)
=> 3y = 6 + x + y ….(eq.2)
=> 3z = -1 + z + t …(eq.3)
=> 3t = 2t + 3 ………..(eq.4)
From (eq.1),
=> 2x = 4
=> x = 2
Substitute x=2 in (eq.2),
=> 3y = 6 + 2 + y
=> 2y = 8
=> y = 4
From (eq.4),
=> t = 3
Substitute t=3 in (eq.3),
=> 3z = -1 + z + 3
=> 2z = 2
=> z = 1
问题19(ii):如果x,y,z和t 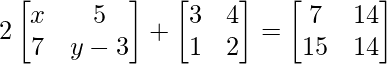 。
。
解决方案:
Given that,
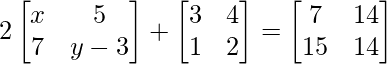
We can arrive at 2 equations from the above matrix equation,
=> 2x + 3 = 7 ………………..(eq.1)
=> 2 (y – 3) + 2 = 14 ….(eq.2)
From (eq.1),
=> 2x = 7 – 3
=> 2x = 4
=> x = 2
From (eq.2),
=> 2y – 6 + 2 = 14
=> 2y = 14 + 4
=> 2y = 18
=> y = 9
问题20:如果X和Y是2×2矩阵,则求解X和Y的以下矩阵方程,2X + 3Y =  ,3X + 2Y =
,3X + 2Y = 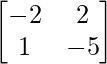 。
。
解决方案:
Let 2X + 3Y = be (eq.1) and let 3X + 2Y =
be (eq.1) and let 3X + 2Y =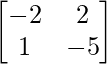 , be (eq.2) .
, be (eq.2) .
=> 2(2X + 3Y) – 3(3X + 2Y) = 4X + 6Y – 9X – 6Y = -5X.
=> -5X =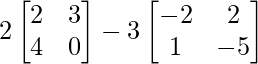
=> -5X =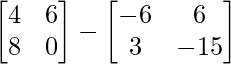
=> -5X =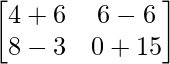
=> -5X =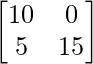
=> 5X =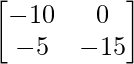
=> X =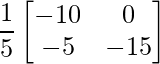
=> X =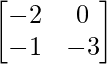
Substitute the matrix X in (eq.1),
=> 3Y =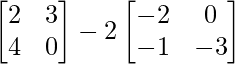
=> 3Y =
=> 3Y =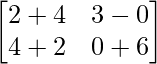
=> 3Y =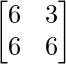
=> Y =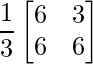
=> Y =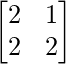
问题21:在某个城市中,有30所大学。每个学院有15个子,6个文员,1个打字员和1个科长。将给定信息表示为列矩阵。使用标量乘法,可以找到所有学院中每种职位的总数。
解决方案:
Let the different posts in each college be represented as :![]()
Now the total posts will be computed as follows:
问题22:Aryan和Babban的月收入比例为3:4,月支出的比例为5:7。如果每个月节省15000,请使用矩阵法找到他们的月收入。
解决方案:
The problem can be solved by considering two matrices, one for expenditure and one for income.
=> The income matrix is: ![]() where x is a constant.
where x is a constant.
=> The expenditure matrix is:![]() where y is a constant.
where y is a constant.
=>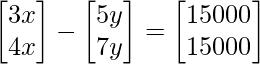
We arrive at 2 equations from the above matrix equation.
=> 3x – 5y = 15000……..(eq.1)
=> 4x – 7y = 15000……..(eq.2)
Solving for y by 4(eq.1) – 3(eq.2),
=> 12x – 20y – 12x + 21y = 4(15000) – 3(15000)
=> y = 15000
Substitute the value of y in (eq.1),
=> 3x = 15000 + 5(15000)
=> 3x = 15000 + 75000
=> 3x = 90000
=> x = 30000
=> Their incomes and expenditures are,
=> 3x = 3(30000) = 90000 and 5y = 5(15000) = 75000
=> 4x = 4(30000) = 120000 and 7y = 7(15000) = 105000