12类RD Sharma解决方案-第五章矩阵代数–练习5.1 |套装2

问题11：找到x，y和z，以便A = B，其中A = 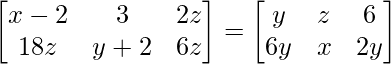$\begin{bmatrix} x-2 & 3 & 2z\\ 18z & y+2 & 6z \end{bmatrix} = \begin{bmatrix} y & z & 6\\ 6y & x & 2y \end{bmatrix}$ 。

解决方案：

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁ : x-2 = y ………….(eq.1)

a₁₂ : z = 3    ………….(eq.2)

a₁₃ : 2z = 6  ………….(eq.3)

a₂₁ : 18z = 6y ……….(eq.4)

a₂₂ : y+2 = x ………..(eq.5)

a₂₃ : 6z = 2y …………(eq.6)

From (eq.2) and (eq.3),

=> z = 3

From (eq.4) and (eq.6),

=> y = 3z

=> y = 3(3)

=> y = 9

Substitute ( y=9 ) in (eq.1),

=> x-2 = 9

=>x = 11

Thus x=11, y=9 and z=3.

问题12：如果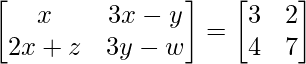$\begin{bmatrix} x & 3x-y\\ 2x+z & 3y-w \end{bmatrix} = \begin{bmatrix} 3 & 2\\ 4 & 7 \end{bmatrix}$ ，找到x，y，z和w。

解决方案：

 As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁ : x = 3      ………….(eq.1)

a₁₂ : 3x-y = 2 ………….(eq.2)

a₂₁ : 2x+z = 4 ………..(eq.3)

a₂₂ : 3y-w = 7 ……….(eq.4)

From (eq.1) ,

=> x = 3

Substitute (x=3) in (eq.2),

=> 3(3)-y = 2

=> y = 3(3) – 2

=> y = 7

Substitute ( x=3 ) in (eq.3),

=> 2(3)+z = 4

=>z = 4-6

=>z = -2

Substitute (y=7) in (eq.4),

=>3(7) – w = 7

=>w = 21 – 7

=>w = 14

Thus x=3, y=7, z=-2 and w=14.

问题13：如果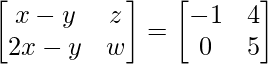$\begin{bmatrix} x-y & z \\ 2x-y & w \end{bmatrix} = \begin{bmatrix} -1 & 4 \\ 0 & 5 \end{bmatrix}$ ，找到x，y，z和w。

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁ : x-y = -1 ………….(eq.1)

a₁₂ : z = 4     ………….(eq.2)

a₂₁ : 2x-y = 0 ………..(eq.3)

a₂₂ : w = 5 …………….(eq.4)

From (eq.2),

=> z = 4

And from (eq.4),

=> w = 5

Now, (eq.1) and (eq.3) form a system of equations comprising of variables x and y. 

Thus, (eq.1) – (eq.2),

=> (x-2x) +(-y+y) = -1 – 0

=> -x = -1

=> x = 1

Substitute (x=1) in (eq.1),

=> 1-y = -1

=>y = 2

Thus, x=1, y=2, z=4 and w=5.

问题14：如果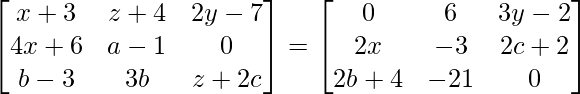$\begin{bmatrix} x+3 & z+4 & 2y-7\\ 4x+6 & a-1 & 0\\ b-3 & 3b & z+2c \end{bmatrix} = \begin{bmatrix} 0 & 6 & 3y-2\\ 2x & -3 & 2c+2\\ 2b+4 & -21 & 0 \end{bmatrix}$ 。获得a，b，c，x，y和z的值。

解决方案：

 As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁ : x+3 = 0 ……………..(eq.1)

a₁₂ : z+4 = 6    ………….(eq.2)

a₁₃ : 2y-7 = 3y-2  ……..(eq.3)

a₂₁ : 4x+6 = 2x ………….(eq.4)

a₂₂ : a-1 = -3 ……………..(eq.5)

a₂₃ : 0 = 2c+2 …………….(eq.6)

a₃₁ : b-3 = 2b+4…………(eq.7)

a₃₂ : 3b = -21………………(eq.8)

a₃₃ : z+2c = 0………………(eq.9)

From (eq.1) and (eq.4),

=> x = -3

From (eq.2) ,

=> z+4 = 6

=> z = 2

From (eq.3),

=> 2y-7 = 3y-2

=> 3y-2y = -7+2

=> y = -5

From (eq.5),

=> a = -3+1

=> a = -2

From (eq.8),

=> 3b = -21

=> b = -7

Substitute (z=2) in (eq.9),

=> 2+ 2c = 0

=> c = -1

Thus, x=-3, y=-5, z=2, a=-2, b=-7 and c=-1.

问题15：如果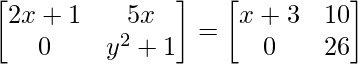$\begin{bmatrix} 2x+1 & 5x \\ 0 & y^2+1 \end{bmatrix} = \begin{bmatrix} x+3 & 10 \\ 0 & 26 \end{bmatrix}$ ，找到(x + y)的值。

解决方案：

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁ : 2x+1 = x+3………..(eq.1)

a₁₂ : 5x = 10 ………………(eq.2)

a₂₁ : 0 = 0  …………………(eq.3)

a₂₂ : y²+1 = 26 …………(eq.4)

From (eq.1) and (eq.2),

=> 2x+1 = x+3

=> x=2

From (eq.4),

=> y²+1 = 26

=> y² = 25

=> y = ± 5

Thus if y = +5,

=> x+y = 7

And if y = -5,

=> x+y = -3

问题16：如果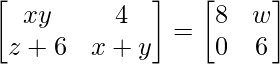$\begin{bmatrix} xy & 4 \\ z+6 & x+y \end{bmatrix} = \begin{bmatrix} 8 & w \\ 0 & 6 \end{bmatrix}$ ，然后找到x，y，z和w的值。

解决方案：

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁ : xy = 8 ……………..(eq.1)

a₁₂ : 4 = w ………………(eq.2)

a₂₁ : z+6 = 0 …………..(eq.3)

a₂₂ : x+y = 6 …………..(eq.4)

From (eq.2),

=> w = 4

And from (eq.3),

=> z = -6

Now, we can see that (eq.1) and (eq.4) form a system of equations comprising of variables x and y.

From (eq.1), 

=> x = 8/y

Substitute (x=8/y) in (eq.4):

=> y + (8/y) = 6

=> y² – 6y +8 = 0

Solving the above equation,

=> y² – 4y – 2y + 8 = 0

=> y( y-4 ) -2( y-4 ) = 0

=> (y – 2)(y – 4) = 0

=> y = 2 or 4

Substitute in (eq.1):

=> when x=2, y=4 and when x=4, y=2.

Thus, (x,y) = (2,4) or (4,2) and z = -6 and w = 4.

问题17(i)：举一个行矩阵的示例，该行矩阵也是一个列矩阵。

解决方案：

We know the order of a row matrix can be written as 1xn (1 row with n elements).

And similarly, the order of a column matrix is mx1.

So, a row matrix which is also a column matrix must be of the order (1×1).

As an example, we can take the matrix : $\begin{bmatrix} 1 \end{bmatrix}$

问题17(ii)：举一个非标量对角矩阵的例子。

解决方案：

In a diagonal matrix, only the diagonal elements possess non-zero values. Thus, for a nxn diagonal matrix, a_ii ≠ 0, for 1≤ i ≤ n.

And a scalar matrix is a diagonal matrix, such that all the diagonal elements are equal.

Thus, a matrix which is diagonal but not scalar is:

$\begin{bmatrix} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 3 \end{bmatrix}$

问题17(iii)：举一个三角矩阵的例子。

解决方案：

A triangular matrix is a square matrix, and it is filled in such a way that, either the triangle above the main-diagonal is non-zero (upper-triangular) or the triangle below the diagonal is non-zero (lower-triangular).

Thus, an example would be : $\begin{bmatrix} 1 & 2 & 3\\ 0 & 1 & 4\\ 0 & 0 & 1 \end{bmatrix}$

问题18：2013年1月，两家汽车经销商的销售数据显示，经销商A售出5辆豪华，3辆高级和4辆标准车，而经销商B出售7辆豪华，2辆优质和3辆标准车。 1-2月当月的总销售量显示，经销商A售出了8辆豪华车，7辆高级车和6辆标准车。在同一2个月内，经销商B售出10辆豪华车，5辆高级车和7辆标准车。编写2×3矩阵，汇总每个经销商在1月和2个月期间的销售数据。

解决方案：

The above data can be represented in the form of tables:

For January 2013,

	Deluxe	Premium	Standard
Dealer A	5	3	4
Dealer B	7	2	3

For January to February,

	Deluxe	Premium	Standard
Dealer A	8	7	6
Dealer B	10	5	7

Thus, the two matrices are : 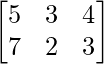$\begin{bmatrix} 5 & 3 & 4\\ 7 & 2 & 3 \end{bmatrix}$ and $\begin{bmatrix} 8 & 7 & 6\\ 10 & 5 & 7 \end{bmatrix}$

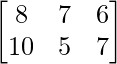
问题19：以下矩阵的x和y值相等?

A = 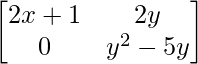$\begin{bmatrix} 2x+1 & 2y \\ 0 & y^2-5y \end{bmatrix}$和B = $\begin{bmatrix} x+3 & y^2+2 \\ 0 & -6 \end{bmatrix}$

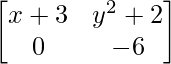
解决方案：

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁ : 2x+1 = x+3 …………(eq.1)

a₁₂ : 2y = y²+2 ……………(eq.2)

a₂₁ : 0 = 0 …………………….(eq.3)

a₂₂ : y²-5y = -6 …………..(eq.4)

From (eq.1),

=> 2x-x = 3-1

=> x=2

Taking (eq.2), it can be re-written as,

=> y²-2y+2 = 0

=> y = 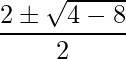$\dfrac {2 \pm \sqrt{4-8}} {2}$

=> y = -1 ± i ( No real solutions )

Taking (eq.4), it can be re-written as,

=> y² – 5y +6 = 0

Solving the equation,

=> y² – 2y – 3y +6 = 0

=> y( y-2 ) -3( y-2 ) = 0

=> ( y-2 )( y-3 ) = 0

=> y = 2 or 3

As values of y are inconsistent, we can say that the above matrices are not equal for any (x,y) pair.

问题20：在以下情况下找到x和y的值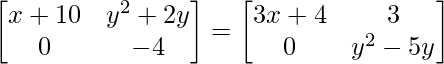$\begin{bmatrix} x+10 & y^2+2y\\ 0 & -4 \end{bmatrix} = \begin{bmatrix} 3x+4 & 3\\ 0 & y^2-5y \end{bmatrix}$ 。

解决方案：

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁ : x+10 = 3x+4 …………(eq.1)

a₁₂ : y²+2y = 3   ……………(eq.2)

a₂₁ : 0 = 0  ……………………..(eq.3)

a₂₂ : y²-5y = -4   …………..(eq.4)

From (eq.1),

=> 2x = 6

=> x = 3

Taking (eq.2), it can be re-written as,

=> y²+2y-3 = 0

=> y² + 3y -y -3 = 0

=> y( y+3 ) -1( y+3 ) = 0

=> ( y+3 )( y-1 ) = 0

=> y = -3 or 1

Taking (eq.3), it can be re-written as,

=> y²-5y+4 = 0

=> y² -4y -y +4 =0

=> y( y-4 ) -1( y-4 ) = 0

=> ( y-4 )( y-1 ) = 0

=> y = 4 or 1

The value of y that can satisfy both (eq.2) and (eq.3) is 1.

=> y=1

Thus, x=3 and y=1.

问题21.如果A = B，则找到a和b的值，其中A = 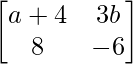$\begin{bmatrix} a+4 & 3b\\ 8 & -6 \end{bmatrix}$ ，B = $\begin{bmatrix} 2a+2 & b^2+2\\ 8 & b^2-5b \end{bmatrix}$ 。

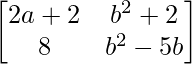解决方案：

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁ : a+4 = 2a+2 …………..(eq.1)

a₁₂ : 3b = b²+2   …………..(eq.2)

a₂₁ : 8 = 8  ……………………..(eq.3)

a₂₂ : -6 = b²-5b   ………….(eq.4)

From (eq.1),

=> a = 2

Taking (eq.2), it can be re-written as,

=> b²-3b+2=0

=> b² – 2b -b +2 = 0

=> b(b-2) -1(b-2) = 0

=> (b-2)(b-1) = 0

=> b=1 or 2

Taking (eq.4) it can be re-written as,

=> b² -5b +6 = 0

=> b² – 3b -2b + 6 = 0

=> b( b-3 ) -2( b-3 ) = 0

=> ( b-3 )( b-2 ) = 0

=> b = 2 or 3

Thus, b=2 can satisfy both (eq.2) and (eq.4).

=> b = 2

Thus, a=2 and b=2.