类12 NCERT解决方案-数学第I部分–第6章导数的应用-练习6.3 |套装1

问题1.在x = 4处找到曲线y的切线的斜率y = 3x ^{4 – 4x。}

解决方案：

Given curve: y = 3x⁴ – 4x

On differentiating w.r.t x, we get

dy/dx = 12x³ – 4

Now, we find the slope of the tangent to the given curve at x = 4 is

= dy/dx = 12(4)³ – 4 = 764

Hence, the slope is 764

问题2：找到曲线切线的斜率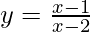$y = \frac{x-1}{x-2}$ ，在x = 10时x≠2。

解决方案：

Given curve: $y=\frac{x-1}{x-2}$

$y=\frac{x-2+1}{x-2}=1+\frac{1}{x-2}$

On differentiating w.r.t x, we get

$\frac{dy}{dx}=0-\frac{1}{(x-2)^2}$

Now, we find the slope of the tangent to the given curve at x = 10 is

$\frac{dy}{dx}=\frac{-1}{(10-2)^2}=\frac{-1}{64}$

Hence, the slope is -1/64

问题3.在x坐标为2的点上找到曲线y = x ^{3 – x + 1的切线的斜率。}

解决方案：

Given curve: y = x³ – x + 1

On differentiating w.r.t x, we get

$\frac{dy}{dx}=\frac{d(x^3-x+1)}{dx}=3x^2-1$

Now, we find the slope of the tangent to the given curve at x = 2 is

$\frac{dy}{dx}=3(2)^2-1=11$

Hence, the slope is 11

问题4.在x坐标为3的点上找到曲线y = x ^{3 –3x + 2的切线的斜率。}

解决方案：

Given curve: y = x³ – 3x + 2

On differentiating w.r.t x, we get

dy/dx = 3x² – 3

Now, we find the slope of the tangent to the given curve at x = 3 is

dy/dx = 3(3)² – 3 = 24

Hence, the slope is 24

问题5.找到法线曲线X = ACOS ^3θ斜率，Y =阿辛在θ=π/ 4 ^3θ。

解决方案：

Given curve: x = acos³θ = f(θ)

y = asin³θ = g(θ)

To find slope of the normal of the curve at θ = π/4

Now, slope of the normal is $\frac{-dx}{dy}$

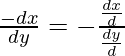$\frac{-dx}{dy}=-\frac{\frac{dx}{dθ}}{\frac{dy}{dθ}}$    -(1)

$\frac{dx}{d\theta} =\frac{d(a\cos^3θ) }{dθ}$ = a.3.cos² θ.(-sin θ)

$\frac{dy}{dθ}=\frac{d(a\sin^3θ)}{dθ}$ = a.3sin² θ.cos θ

$\frac{-dx}{dθ}=\frac{a.3.\cos^2θ.(-\sinθ)}{a.3.\sin^2θ.\cosθ}$      -(using eq(1))

$\frac{-dx}{dy}=\frac{\cosθ}{\sinθ}=\cotθ$

Now, we find the slope of the tangent to the given curve at θ = π/4 is

$\frac{-dx}{dy}=\cot(\frac{π}{4})=1$

The slope of normal of the parametric curve

Hence, the slope is 1

问题6.求曲线法线的斜率x = 1 –asinθ，y = bcos ^2θ ，θ=π/ 2。

解决方案：

Given curve: x = 1 – a sinθ

y = b cos2θ

Now, slope of normal is $\frac{-dx}{dy}$

$\frac{-dx}{dy}=\frac{\frac{-dx}{dθ}}{\frac{dy}{dθ}}$          -(1)

$\frac{dx}{dθ}=\frac{d(1-a\sinθ)}{dθ}=-a\cosθ$

$\frac{dy}{dθ}=\frac{d(b\cos^2θ)}{dθ}=-2b\cosθ\sinθ$

$\frac{-dx}{dy}=\frac{-a\cosθ}{-2b\cosθ\sinθ}$        -(using eq(1))

$\frac{-dx}{dy}=\frac{-a}{2b\sinθ}$

Now, we find the slope of the tangent to the given curve at θ = π/2 is

$\frac{-dx}{dy}=\frac{-a}{2b\sin\frac{π}{2}}=\frac{-a}{2b}$

Hence, the slope is -a/2b.

问题7.找到曲线y = x ³ – 3x ² – 9x + 7的切线平行于x轴的点。

解决方案：

Given curve: y = x³ – 3x² – 9x + 7

On differentiating w.r.t x, we get

dy/dx = 3x² – 6x – 9

For tangent to be parallel to x-axis, slope is 0. So dy/dx = 0.

3x² – 6x – 9 = 0

3(x² – 2x – 3) = 0

3(x² + x – 3x – 3) = 0

3(x(x + 1) – 3(x + 1)) = 0

3(x + 1)(x – 3) = 0

x = -1 or x = 3

For x = -1, y = (-1)³ – 3(-1)² – 9(-1) + 7

x = -1, y = -1 – 3 + 9 + 7 = 12

Hence, the first point is (-1, 12)

问题8.在曲线y =(x – 2) ²上找到一个点，在该点处切线平行于连接点(2，0)和(4，4)的弦。

解决方案：

Given curve: y = (x – 2)²

On differentiating w.r.t x, we get

dy/dx = 2(x – 2)                 -(1)

Given that, the tangent is parallel to the chord joining the points (2, 0) & (4, 4)

Slope of the chord = $\frac{y_2-y_1}{x_2-x_1}=\frac{4-0}{4-2}=\frac{4}{2}=2$

Now equality dy/dx = slope of chord

2(x – 2) = 2

x – 2 = 1

x = 3

y = (x – 2)²

y = (3 – 2)² = 1

Hence, the point on the curve y = (x – 2)² is (3, 1)

问题9.在曲线y = x ³ – 11x + 5上找到切线为y = x – 11的点。

解决方案：

Given curve: y = x³ – 11x + 5

Given tangent: y = x – 11

From the given tangent, we can find out the slope comparing y = x – 11 with y = mx + c, we get

Slope(m) = 1

Now y = x³ – 11x + 5

dy/dx = 3x² – 11                  -(1)

dy/dx = slope = 1

So, from eq(1), we get  

3x² – 11 = 1

3x² = 12

x² = 4

x = ±2

If x = +2, y = 2³ – 11(2) + 5 = -9

If x = -2, y = (-2)³ – 11(-2) + 5 = 19

The points must lie on the tangent as well.

Only (2,-9) is satisfying the tangent equation.

So the point on the curve whose tangent is y = x – 11 is (2,-9). 

问题10。找到所有具有斜率–1且与曲线y =切线的直线的方程式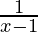$\frac{1}{x-1}$ [Tex] [/ Tex]，x≠1。

解决方案：

Given curve: y = $\frac{1}{x-1}$

$\frac{dy}{dx}=\frac{-1}{(x-1)^2}$                  -(1)

Now given slope = -1 & we know that dy/dx = slope, so

dy/dx = -1                  -(1)

From 1 & 2, we get

-1 = $\frac{-1}{(x-1)^2}$

(x – 1)² = 1

x = 1 ± 1

x₁ = 2 & x₂ = 0

Now corresponding to these x₁ & x₂ we need to find out y₁ & y₂ 

$y_1=\frac{1}{x-1}=\frac{1}{2-1}=1$

$y_2=\frac{1}{x_2-1}=\frac{1}{0-1}=-1$

The points are (2, 1) & (0, -1)

Now equations slope is -1

Using point slope form the first tangent equation is 

(y – y₁) = m(x – x₁)

y – 1 = -1(x – 2)

= x + y = 3

Using point slope from the second tangent equation is 

(y – y₂) = m(x – x₂)

y – (-1) = -1(x – 0)

= x + y + 1 = 0 

问题11。找到所有与曲线相切的，具有斜率2的线的方程式$y = \frac{1}{x-3}$ ，x≠3。

解决方案：

Given curve: y = 1/(x – 3) 

dy/dx = -1/(x – 3)² = slope               -(dy/dx is slope)

Now given slope is 2, so

dy/dx = -1/(x – 3)² = 2

(x – 3)² = -1/2              -(1) (not possible)

Now because there is no real value of x which can satisfy 1, therefore no such tangent exists on the curve y = 1/x – 3 whose is 2.

问题12.找到斜率为0且与曲线相切的直线的方程式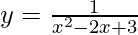$y=\frac{1}{x^2-2x+3}$ 。

解决方案：

Given curve,

$y=\frac{1}{x^2-2x+3}$ 

On differentiating w.r.t x, we get

$\frac{dy}{dx}=\frac{-1}{(x^2-2x+3)}.(2x-2)$      -(chain rule)

Given slope = 0 = dy/dx  

So,$\frac{dy}{dx}=\frac{-2(x-1)}{(x^2-2x+3)^2}=0$

x – 1 = 0

x = 1

For x = 1, y = $\frac{1}{1^2-2(1)+3}=\frac{1}{2}$

So the equation of tangent from point slope from is 

y – y₁ = m(x – x₁)

$y-\frac{1}{2}$= 0(x – 1)

2y – 1 = 0

问题13：在曲线上找到点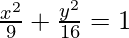$\frac{x^2}{9}+\frac{y^2}{16}=1$切线所在的位置

(i)与x轴平行(ii)与y轴平行

解决方案：

Given curve:

$\frac{x^2}{9}+\frac{y^2}{16}=1$         -(1)

(i) If tangent is parallel to x-axis then it means slope is 0 or dy/dx = 0

On differentiating both sides of equations (1) we get,

$\frac{2x}{9}+\frac{2y}{16}.\frac{dy}{dx}=0$ 

$\frac{dy}{dx}=\frac{-16x}{9y}$

Now slope = 0, so

$\frac{-16x}{9y}=0$

= x₁ = 0

For x₁ = 0,   

$\frac{0^2}{9}+\frac{y_1^2}{16}=1$

y₁² = 16

y₁ = ±4

The coordinates are (0, 4) & (0, -4)

(ii) Now, if tangent is parallel to y-axis to the dy/dx or slope is not defined or dy/dx = 0

On differentiating equations(1) with respect to y, we get

$\frac{2x}{9}.\frac{dx}{dy}+\frac{2y}{16}=0$ 

$\frac{dx}{dy}=0,\frac{-9y}{16x}=0$

y₂ = 0

For y₂ = 0, $\frac{x_2^2}{9}+\frac{0}{16}=1$

x₂² = 9

x₂ = ±3

Hence, the coordinates are (3, 0) & (-3, 0)

第6章衍生物的应用-练习6.3 |套装2