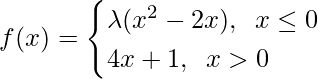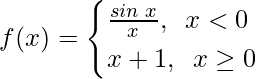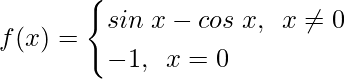问题18:对于λ的哪个值,该函数定义为
连续于x = 0?那么在x = 1时的连续性又如何呢?
解决方案:
To be continuous function, f(x) should satisfy the following at x = 0:
![]()
Continuity at x = 0,
Left limit = ![]()
= λ(02– 2(0)) = 0
Right limit = ![]()
= λ4(0) + 1 = 1
Function value at x = 0, f(0) = ![]()
As, 0 = 1 cannot be possible
Hence, for no value of λ, f(x) is continuous.
But here, ![]()
Continuity at x = 1,
Left limit = ![]()
= (4(1) + 1) = 5
Right limit = ![]()
= 4(1) + 1 = 5
Function value at x = 1, f(1) = 4(1) + 1 = 5
As, ![]()
Hence, the function is continuous at x = 1 for any value of λ.
问题19:证明由g(x)= x – [x]定义的函数在所有积分点上都是不连续的。此处[x]表示小于或等于x的最大整数。
解决方案:
[x] is greatest integer function which is defined in all integral points, e.g.
[2.5] = 2
[-1.96] = -2
x-[x] gives the fractional part of x.
e.g: 2.5 – 2 = 0.5
c be an integer
Let’s check the continuity at x = c,
Left limit = ![]()
= (c – (c – 1)) = 1
Right limit = ![]()
= (c – c) = 0
Function value at x = c, f(c) = c – = c – c = 0
As, ![]()
Hence, the function is discontinuous at integral.
c be not an integer
Let’s check the continuity at x = c,
Left limit = ![]()
= (c – (c – 1)) = 1
Right limit = ![]()
= (c – (c – 1)) = 1
Function value at x = c, f(c) = c – = c – (c – 1) = 1
As, ![]()
Hence, the function is continuous at non-integrals part.
问题20.由f(x)= x 2 – sin x + 5定义的函数在x =π处连续吗?
解决方案:
Let’s check the continuity at x = π,
f(x) = x2 – sin x + 5
Let’s substitute, x = π+h
When x⇢π, Continuity at x = π
Left limit = ![]()
= (π2 – sinπ + 5) = π2 + 5
Right limit = ![]()
= (π2 – sinπ + 5) = π2 + 5
Function value at x = π, f(π) = π2 – sin π + 5 = π2 + 5
As, ![]()
Hence, the function is continuous at x = π .
问题21.讨论以下功能的连续性:
(a)f(x)= sin x + cos x
解决方案:
Here,
f(x) = sin x + cos x
Let’s take, x = c + h
When x⇢c then h⇢0
![]()
So,
![]() (sin(c + h) + cos(c + h))
(sin(c + h) + cos(c + h))
Using the trigonometric identities, we get
sin(A + B) = sin A cos B + cos A sin B
cos(A + B) = cos A cos B – sin A sin B
![]() ((sinc cosh + cosc sinh) + (cosc cosh − sinc sinh))
((sinc cosh + cosc sinh) + (cosc cosh − sinc sinh))
![]() = ((sinc cos0 + cosc sin0) + (cosc cos0 − sinc sin0))
= ((sinc cos0 + cosc sin0) + (cosc cos0 − sinc sin0))
cos 0 = 1 and sin 0 = 0
![]() = (sinc + cosc) = f(c)
= (sinc + cosc) = f(c)
Function value at x = c, f(c) = sinc + cosc
As, ![]() = f(c) = sinc + cosc
= f(c) = sinc + cosc
Hence, the function is continuous at x = c.
(b)f(x)= sin x – cos x
解决方案:
Here,
f(x) = sin x – cos x
Let’s take, x = c+h
When x⇢c then h⇢0
![]()
So,
![]() (sin(c + h) − cos(c + h))
(sin(c + h) − cos(c + h))
Using the trigonometric identities, we get
sin(A + B) = sin A cos B + cos A sin B
cos(A + B) = cos A cos B – sin A sin B
![]() ((sinc cosh + cosc sinh) − (cosc cosh − sinc sinh))
((sinc cosh + cosc sinh) − (cosc cosh − sinc sinh))
![]() = ((sinc cos0 + cosc sin0) − (cosc cos0 − sinc sin0))
= ((sinc cos0 + cosc sin0) − (cosc cos0 − sinc sin0))
cos 0 = 1 and sin 0 = 0
![]() = (sinc − cosc) = f(c)
= (sinc − cosc) = f(c)
Function value at x = c, f(c) = sinc − cosc
As, ![]() = f(c) = sinc − cosc
= f(c) = sinc − cosc
Hence, the function is continuous at x = c.
(c)f(x)= sin x。 cos x
解决方案:
Here,
f(x) = sin x + cos x
Let’s take, x = c+h
When x⇢c then h⇢0
![]()
So,
![]() sin(c + h) × cos(c + h))
sin(c + h) × cos(c + h))
Using the trigonometric identities, we get
sin(A + B) = sin A cos B + cos A sin B
cos(A + B) = cos A cos B – sin A sin B
![]() ((sinc cosh + cosc sinh) × (cosc cosh − sinc sinh))
((sinc cosh + cosc sinh) × (cosc cosh − sinc sinh))
![]() = ((sinc cos0 + cosc sin0) × (cosc cos0 − sinc sin0))
= ((sinc cos0 + cosc sin0) × (cosc cos0 − sinc sin0))
cos 0 = 1 and sin 0 = 0
![]() = (sinc × cosc) = f(c)
= (sinc × cosc) = f(c)
Function value at x = c, f(c) = sinc × cosc
As, ![]() = f(c) = sinc × cosc
= f(c) = sinc × cosc
Hence, the function is continuous at x = c.
问题22.讨论余弦,割线,割线和切线函数的连续性。
解决方案:
Continuity of cosine
Here,
f(x) = cos x
Let’s take, x = c+h
When x⇢c then h⇢0
![]()
So,
![]()
Using the trigonometric identities, we get
cos(A + B) = cos A cos B – sin A sin B
![]() (cosc cosh − sinc sinh)
(cosc cosh − sinc sinh)
![]() = (cosc cos0 − sinc sin0)
= (cosc cos0 − sinc sin0)
cos 0 = 1 and sin 0 = 0
![]() = (cosc) = f(c)
= (cosc) = f(c)
Function value at x = c, f(c) = (cosc)
As, ![]() = f(c) = (cosc)
= f(c) = (cosc)
Hence, the cosine function is continuous at x = c.
Continuity of cosecant
Here,
f(x) = cosec x = ![]()
Domain of cosec is R – {nπ}, n ∈ Interger
Let’s take, x = c + h
When x⇢c then h⇢0
![]()
So,
![]()
Using the trigonometric identities, we get
sin(A + B) = sin A cos B + cos A sin B

cos 0 = 1 and sin 0 = 0
![]()
Function value at x = c, f(c) = ![]()
As, ![]()
Hence, the cosecant function is continuous at x = c.
Continuity of secant
Here,
f(x) = sec x = ![]()
Let’s take, x = c + h
When x⇢c then h⇢0
![]()
So,
![]()
Using the trigonometric identities, we get
cos(A + B) = cos A cos B – sin A sin B
![]()
![]()
cos 0 = 1 and sin 0 = 0
![]()
Function value at x = c, f(c) = ![]()
As, ![]()
Hence, the secant function is continuous at x = c.
Continuity of cotangent
Here,
f(x) = cot x = ![]()
Let’s take, x = c+h
When x⇢c then h⇢0
![]()
So,
![]()
Using the trigonometric identities, we get
sin(A + B) = sin A cos B + cos A sin B
cos(A + B) = cos A cos B – sin A sin B
![]()
![]()
cos 0 = 1 and sin 0 = 0
![]()
![]()
Function value at x = c, f(c) = ![]()
As, ![]()
Hence, the cotangent function is continuous at x = c.
问题23:找出f的所有不连续点,其中
解决方案:
Here,
From the two continuous functions g and h, we get
![]() = continuous when h(x) ≠ 0
= continuous when h(x) ≠ 0
For x < 0, f(x) = ![]() , is continuous
, is continuous
Hence, f(x) is continuous x ∈ (-∞, 0)
Now, For x ≥ 0, f(x) = x + 1, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (0, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 0) U (0, ∞)= R – {0}
Let’s check the continuity at x = 0,
Left limit = 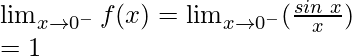
Right limit = 
Function value at x = 0, f(0) = 0 + 1 = 1
As, ![]()
Hence, the function is continuous at x = 0.
Hence, the function is continuous for any real number.
问题24.确定f是否定义为
是连续函数吗?
解决方案:
Here, as it is given that
For x = 0, f(x) = 0, which is a constant
As constant are continuous, hence f(x) is continuous x ∈ = R – {0}
Let’s check the continuity at x = 0,
As, we know range of sin function is [-1,1]. So, -1 ≤ ![]() ≤ 1 which is a finite number.
≤ 1 which is a finite number.
Limit = ![]()
= (02 ×(finite number)) = 0
Function value at x = 0, f(0) = 0
As, ![]()
Hence, the function is continuous for any real number.
问题25.检查f的连续性,其中f定义为
解决方案:
Continuity at x = 0,
Left limit = ![]()
= (sin0 − cos0) = 0 − 1 = −1
Right limit = ![]()
= (sin0 − cos0) = 0 − 1 = −1
Function value at x = 0, f(0) = sin 0 – cos 0 = 0 – 1 = -1
As, ![]()
Hence, the function is continuous at x = 0.
Continuity at x = c (real number c≠0),
Left limit = ![]()
= (sinc − cosc)
Right limit = ![]()
= (sinc − cosc)
Function value at x = c, f(c) = sin c – cos c
As, ![]()
So concluding the results, we get
The function f(x) is continuous at any real number.
找到k的值,以使函数f在练习26至29中的指定点处连续。
问题26。  在x = π/ 2。
在x = π/ 2。
解决方案:
Continuity at x = π/2
Let’s take x = ![]()
When x⇢π/2 then h⇢0
Substituting x = ![]() +h, we get
+h, we get
cos(A + B) = cos A cos B – sin A sin B
Limit = 
Function value at x = ![]() = 3
= 3
As, ![]() should satisfy, for f(x) being continuous
should satisfy, for f(x) being continuous
k/2 = 3
k = 6
问题27。  在x = 2
在x = 2
解决方案:
Continuity at x = 2
Left limit = ![]()
= k(2)2 = 4k
Right limit = 
Function value at x = 2, f(2) = k(2)2 = 4k
As, ![]() should satisfy, for f(x) being continuous
should satisfy, for f(x) being continuous
4k = 3
k = 3/4
问题28。  在x =π处
在x =π处
解决方案:
Continuity at x = π
Left limit = ![]()
= k(π) + 1
Right limit = ![]()
= cos(π) = -1
Function value at x = π, f(π) = k(π) + 1
As, ![]() should satisfy, for f(x) being continuous
should satisfy, for f(x) being continuous
kπ + 1 = -1
k = -2/π
问题29。  在x = 5
在x = 5
解决方案:
Continuity at x = 5
Left limit = ![]()
= k(5) + 1 = 5k + 1
Right limit = ![]()
= 3(5) – 5 = 10
Function value at x = 5, f(5) = k(5) + 1 = 5k + 1
As, ![]() should satisfy, for f(x) being continuous
should satisfy, for f(x) being continuous
5k + 1 = 10
k = 9/5
问题30.找到a和b的值,使得由定义的函数
是一个连续的函数
解决方案:
Continuity at x = 2
Left limit = 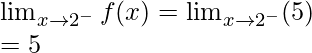
Right limit = 
Function value at x = 2, f(2) = 5
As, ![]() should satisfy, for f(x) being continuous at x = 2
should satisfy, for f(x) being continuous at x = 2
2a + b = 5 ……………………(1)
Continuity at x = 10
Left limit = ![]()
= 10a + b
Right limit = ![]()
= 21
Function value at x = 10, f(10) = 21
As, ![]() should satisfy, for f(x) being continuous at x = 10
should satisfy, for f(x) being continuous at x = 10
10a + b = 21 ……………………(2)
Solving the eq(1) and eq(2), we get
a = 2
b = 1
问题31.证明由f(x)= cos(x 2 )定义的函数是一个连续函数
解决方案:
Let’s take
g(x) = cos x
h(x) = x2
g(h(x)) = cos (x2)
To prove g(h(x)) continuous, g(x) and h(x) should be continuous.
Continuity of g(x) = cos x
Let’s check the continuity at x = c
x = c + h
g(c + h) = cos (c + h)
When x⇢c then h⇢0
cos(A + B) = cos A cos B – sin A sin B
Limit =  (cosc cosh − sinc sinh)
(cosc cosh − sinc sinh)
= cosc cos0 − sinc sin0 = cosc
Function value at x = c, g(c) = cos c
As, ![]()
The function g(x) is continuous at any real number.
Continuity of h(x) = x2
Let’s check the continuity at x = c
Limit = ![]()
= c2
Function value at x = c, h(c) = c2
As, ![]()
The function h(x) is continuous at any real number.
As, g(x) and h(x) is continuous then g(h(x)) = cos(x2) is also continuous.
问题32.证明由f(x)= |定义的函数cos x |是连续函数。
解决方案:
Let’s take
g(x) = |x|
m(x) = cos x
g(m(x)) = |cos x|
To prove g(m(x)) continuous, g(x) and m(x) should be continuous.
Continuity of g(x) = |x|
As, we know that modulus function works differently.
In |x – 0|, |x| = x when x ≥ 0 and |x| = -x when x < 0
Let’s check the continuity at x = c
When c < 0
Limit = 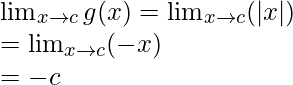
Function value at x = c, g(c) = |c| = -c
As, ![]()
When c ≥ 0
Limit = 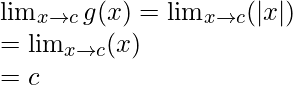
Function value at x = c, g(c) = |c| = c
As, ![]()
The function g(x) is continuous at any real number.
Continuity of m(x) = cos x
Let’s check the continuity at x = c
x = c + h
m(c + h) = cos (c + h)
When x⇢c then h⇢0
cos(A + B) = cos A cos B – sin A sin B
Limit = 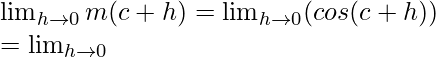 (cosc cosh − sinc sinh)
(cosc cosh − sinc sinh)
= cosc cos0 − sinc sin0 = cosc
Function value at x = c, m(c) = cos c
As, ![]()
The function m(x) is continuous at any real number.
As, g(x) and m(x) is continuous then g(m(x)) = |cos x| is also continuous.
问题33.检查罪孽| x |是连续函数。
解决方案:
Let’s take
g(x) = |x|
m(x) = sin x
m(g(x)) = sin |x|
To prove m(g(x)) continuous, g(x) and m(x) should be continuous.
Continuity of g(x) = |x|
As, we know that modulus function works differently.
In |x-0|, |x|=x when x≥0 and |x|=-x when x<0
Let’s check the continuity at x = c
When c < 0
Limit = 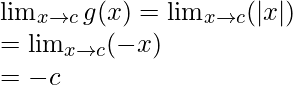
Function value at x = c, g(c) = |c| = -c
As, ![]()
When c ≥ 0
Limit = 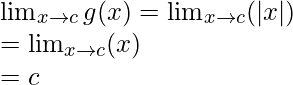
Function value at x = c, g(c) = |c| = c
As, ![]()
The function g(x) is continuous at any real number.
Continuity of m(x) = sin x
Let’s check the continuity at x = c
x = c + h
m(c + h) = sin (c + h)
When x⇢c then h⇢0
sin(A + B) = sin A cos B + cos A sin B
Limit = 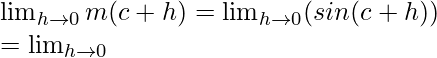 (sinc cosh + cosc sinh)
(sinc cosh + cosc sinh)
= sinc cos0 + cos csin0 = sinc
Function value at x = c, m(c) = sin c
As, ![]()
The function m(x) is continuous at any real number.
As, g(x) and m(x) is continuous then m(g(x)) = sin |x| is also continuous.
问题34.找出f(x)= |定义的f的所有不连续点。 x | – | x + 1 |
解决方案:
Let’s take
g(x) = |x|
m(x) = |x + 1|
g(x) – m(x) = | x | – | x + 1 |
To prove g(x) – m(x) continuous, g(x) and m(x) should be continuous.
Continuity of g(x) = |x|
As, we know that modulus function works differently.
In |x – 0|, |x| = x when x≥0 and |x| = -x when x < 0
Let’s check the continuity at x = c
When c < 0
Limit = 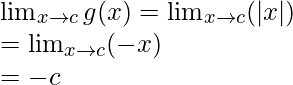
Function value at x = c, g(c) = |c| = -c
As, ![]()
When c ≥ 0
Limit = 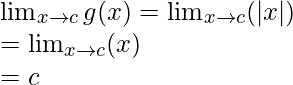
Function value at x = c, g(c) = |c| = c
As, ![]()
The function g(x) is continuous at any real number.
Continuity of m(x) = |x + 1|
As, we know that modulus function works differently.
In |x + 1|, |x + 1| = x + 1 when x ≥ -1 and |x + 1| = -(x + 1) when x < -1
Let’s check the continuity at x = c
When c < -1
Limit = 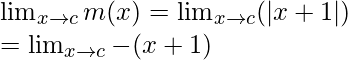
= -(c + 1)
Function value at x = c, m(c) = |c + 1| = -(c + 1)
As, ![]()
When c ≥ -1
Limit = 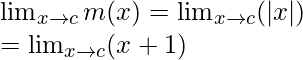
= c + 1
Function value at x = c, m(c) = |c| = c + 1
As, ![]() = m(c) = c + 1
= m(c) = c + 1
The function m(x) is continuous at any real number.
As, g(x) and m(x) is continuous then g(x) – m(x) = |x| – |x + 1| is also continuous.