将练习1到11中的函数分开。
问题1.(3 x 2 – 9x – 5) 9
解决方案:
Let us assume y = (3x2 – 9x – 5)9
Now, differentiate w.r.t x
![]()
Using chain rule, we get
= 9(3x2 – 9 x + 5)8 ![]()
= 9(3x2 – 9x + 5)8.(6x – 9)
= 9(3x 2 – 9x + 5)8.3(2x – 3)
= 27(3x2 – 9x + 5)8 (2x – 3)
问题2.罪3 x + cos 6 x
解决方案:
Let us assume y = sin3 x + cos6 x
Now, differentiate w.r.t x
![]()
Using chain rule, we get
= ![]()
= ![]()
= 3 sin2 x. cos x + 6 cos5 x.(-sin x)
= 3 sin x cos x(sin x – 2 cos4 x)
问题3. 5x 3 cos 2 x
解决方案:
Let us assume y = 5x3 cos 2x
Now we’re taking logarithm on both the sides
logy = 3 cos 2 x log 5 x
Now, differentiate w.r.t x
![]()
![]()
![]()
![]()
![]()
问题4. sin -1 (x√x),0≤x≤1
解决方案:
Let us assume y = sin-1(x√x)
Now, differentiate w.r.t x
![]()
Using chain rule, we get
=![]()
=![]()
=![]()
=![]()
=![]()
问题5 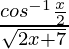 ,-2
,-2
解决方案:
Let us assume y =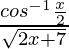
Now, differentiate w.r.t x and by quotient rule, we obtain
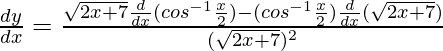
= ![Rendered by QuickLaTeX.com \frac{\sqrt{2x+7}[\frac{-1}{\sqrt{1-(\frac{x}{2})^2}}.\frac{d}{dx}(\frac{x}{2})]-(cos^{-1}\frac{x}{2})\frac{1}{2\sqrt{2x+7}}.\frac{d}{dx}(2x+7)}{2x+\frac{7}{2}}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_19.jpg)
= ![Rendered by QuickLaTeX.com \frac{\sqrt{2x+7}\frac{-1}{\sqrt{4-x^2}}-[cos^{-1}\frac{x}{2}]\frac{2}{2\sqrt{2x+7}}}{2x+7}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_20.jpg)
= 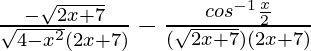
= ![Rendered by QuickLaTeX.com -[\frac{1}{\sqrt{4-x^2}\sqrt{2x+7}}+\frac{cos^{-1}\frac{x}{2}}{(2x+7)^\frac{1}{2}}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_22.jpg)
问题6。 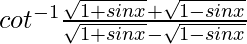 ,0
,0 π/ 2
解决方案:
Let us assume y = 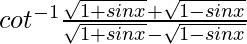 ……(1)
……(1)
Now solve 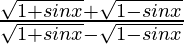
= 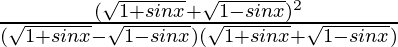
= 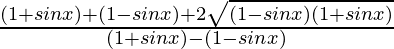
= 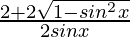
= 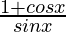
= 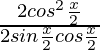
= cotx/2
Now put this value in eq(1), we get
y = cot-1(cotx/2)
y = x/2
Now, differentiate w.r.t x
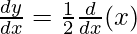
dy/dx = 1/2
问题7.(log x) log x ,x> 1
解决方案:
Let us assume y = (log x)log x
Now we are taking logarithm on both sides,
log y = log x .log(log x)
Now, differentiate w.r.t x on botj side, we get
![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[logx.log(logx)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_32.jpg)
![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=log(logx).\frac{d}{dx}(log x)+logx.\frac{d}{dx}[log(logx)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_33.jpg)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=y[log(logx).\frac{1}{x}+logx.\frac{1}{logx}.\frac{d}{dx}(logx)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_34.jpg)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=y[\frac{1}{x}log(logx)+\frac{1}{x}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_35.jpg)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(logx)^{logx}[\frac{1}{x}+\frac{log(logx)}{x}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_36.jpg)
问题8.对于某些常数a和b,cos(a cos x + b sin x)。
解决方案:
Let us assume y = cos(a cos x + b sin x)
Now, differentiate w.r.t x
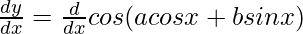
By using chain rule, we get
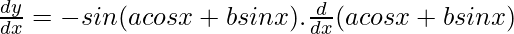
= -sin x(a cos x + b sin x).[a (-sin x) + b cos x]
= (a sin x – b cos x).sin (a cos x + b sin x)
问题9.(sin x – cos x) (sin x – cos x) , π/ 4
解决方案:
Let us assume y = (sin x – cos x)(sin x – cos x)
Now we are taking logarithm on both sides,
log y = (sin x – cos x).log(sin x – cos x)
Now, differentiate w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[(sinx-cosx)log(sinx-cosx)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_39.jpg)
Using chain rule, we get
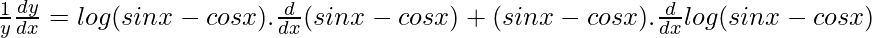
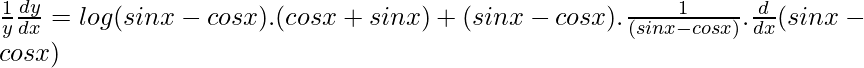
dy/dx = (sinx – cosx)(sinx – cosx)[(cosx + sinx).log(sinx – cosx) + (cosx + sinx)]
dy/dx = (sinx – cosx)(sinx – cosx)(cosx + sinx)[1 + log (sinx – cosx)]
问题10. x x + x a + a x + a对于某些固定的a> 0和x> 0
解决方案:
Let us assume y = xx + xa + ax + aa
Also, let us assume xx = u, xa = v, ax = w, aa = s
Therefore, y = u + v + w + s
So, on differentiating w.r.t x, we get
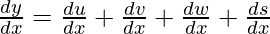 ……….(1)
……….(1)
So first we solve: u = xx
Now we are taking logarithm on both sides,
log u = log xx
log u = x log x
On differentiating both sides w.r.t x, we get
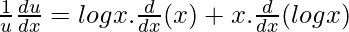
![Rendered by QuickLaTeX.com \frac{du}{dx}=u[logx.1+x.\frac{1}{x}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_44.jpg)
du/dx = xx[logx + 1] = xx(1 + logx) …….(2)
Now we solve: v = xa
On differentiating both sides w.r.t x, we get
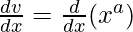
dv/dx = ax(a – 1) ……(3)
Now we solve: w = ax
Now we are taking logarithm on both sides,
log w =log a x
log w = x log a
On differentiating both sides w.r.t x, we get
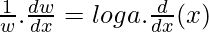
dw/dx = w loga
dw/dx = axloga ………(4)
Now we solve: s = a a
So, on differentiating w.r.t x, we get
ds/dx = 0 ………(5)
Now put all these values from eq(2), (3), (4), (5) in eq(1), we get
dy/dx = xx(1 + logx) + ax(a – 1) + axloga + 0
= xx (1 + log x) + axa -1 + ax log a
问题11.区分wrt x, 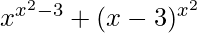 ,对于x> 3
,对于x> 3
解决方案:
Let us assume y =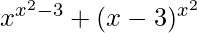
Also let us considered u = 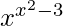 and v =
and v = 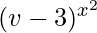
so, y = u + v
On differentiating both side w.r.t x, we get
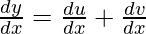 …….(1)
…….(1)
So, now we solve, u = 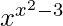
Now we are taking logarithm on both sides,
log u = log 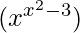
log u = (x 2 – 3) log x
On differentiating w.r.t x, we get
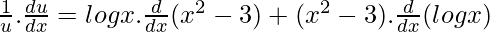
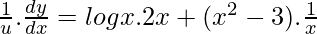
=![Rendered by QuickLaTeX.com \frac{du}{dx}= x^{x^2-3}.[\frac{x^2-3}{x}+ 2xlogx]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_56.jpg) …….(2)
…….(2)
Now we solve: v = 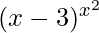
Now we are taking logarithm on both sides,
log v = 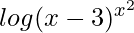
log v = x2 log(x – 3)
On differentiating both sides w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{1}{v}.\frac{dv}{dx}= log (x-3).\frac{d}{dx}(x^2)+x^2\frac{d}{dx}[log(x-3)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_59.jpg)
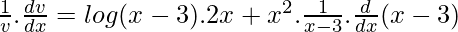
![Rendered by QuickLaTeX.com \frac{dv}{dx}=v[2xlog(x-3)+\frac{x^2}{x-3}.1]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_61.jpg)
![Rendered by QuickLaTeX.com \frac{dv}{dx}=(x-3)^{x^2}[\frac{x^2}{x-3}+2xlog(x-3)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_62.jpg) …..(3)
…..(3)
Now put all these values from eq(2), and (3) in eq(1), we get
![Rendered by QuickLaTeX.com \frac{dy}{dx}= x^{x^2-3}[\frac{x^2-3}{x}+2xlogx]+(x-3)^{x^2}[\frac{x^2}{x-3}+2xlog(x-3)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_63.jpg)
问题12.如果y = 12(1-cos t),x = 10(t-sin t),- π/ 2
解决方案:
According to the question
y = 12(1 – cos t) ……(1)
x = 10 (t – sin t) ……(2)
So, \frac{dy}{dx}= \frac{\frac{dy}{dt}}{\frac{dx}{dt}} ……(3)
On differentiating eq(1) w.r.t t, we get
![Rendered by QuickLaTeX.com \frac{dy}{dt} = \frac{d}{dt} [12 (1 - cost)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_64.jpg)
= 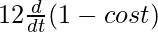
= 12.[0 – (- sin t)]
= 12 sin t
On differentiating eq(2) w.r.t t, we get
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\frac{d}{dt}[10. (t - sin t)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_66.jpg)
= 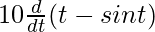
= 10(1 – cos t)
Now put the value of dy/dt and dx/dt in eq(3), we get
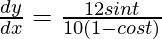
= 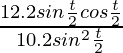
= 6/5 cot t/2
问题13查找DY / DX,如果y = -1罪X +罪-1√1-X 2,0
解决方案:
According to the question
y = sin-1 x + sin-1√1 – x2
On differentiating w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{d}{dx}[sin^{-1}x+sin ^{-1}\sqrt{1-x^2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_70.jpg)
Using chain rule, we get
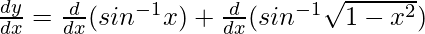
= 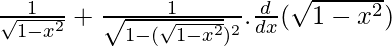
= 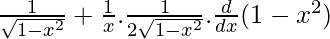
= 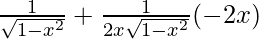
= 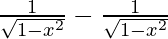
dy/dx = 0
问题14.如果x√1+ y +y√1+ x = 0,则-1
解决方案:
According to the question
x√1 + y = -y√1 + x
On squaring both sides, we get
x2 (1 + y) = y2 (1 + x)
⇒ x2 + x2 y = y2 + x y2
⇒ x2 – y2 = xy 2 – x2 y
⇒ x2 – y2 = xy (y – x)
⇒ (x + y)(x – y) = xy (y – x)
⇒ x + y = -xy
⇒ (1 + x) y = -x
⇒ y = -x/(1 + x)
On differentiating both sides w.r.t x, we get
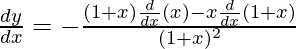
= 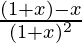
= 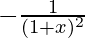
Hence proved.
问题15。如果(x – a) 2 +(y – b) 2 = c 2 ,则对于某些c> 0,证明![由QuickLaTeX.com渲染 \frac{[1+(\frac{dy}{dx})^2]^\frac{3}{2}} {\frac{d^2y}{dx^2}}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_80.jpg) 是一个独立于a和b的常数。
是一个独立于a和b的常数。
解决方案:
According to the question
(x – a)2+ (y – b)2= c2
On differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d}{dx}[(x-a)^2]+\frac{d}{dx}[(y-b)^2]=\frac{d}{dx}(c^2)](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_81.jpg)
⇒ 2(x – a).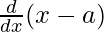 + 2(y – b)
+ 2(y – b)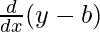 = 0
= 0
⇒ 2(x – a).1 + 2(y – b).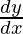 = 0
= 0
⇒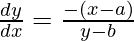 …….(1)
…….(1)
Again on differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2} = \frac{d}{dx}[\frac{-(x-a)}{y-b}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_86.jpg)
![Rendered by QuickLaTeX.com = -[\frac{(y-b).\frac{d}{dx}(x-a)-(x-a).\frac{d}{dx}(y-b)}{(y-b)^2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_87.jpg)
![Rendered by QuickLaTeX.com =-[\frac{(y-b)-(x-a).\frac{dy}{dx}}{(y-b)^2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_88.jpg)
![Rendered by QuickLaTeX.com = -[\frac{(y-b)-(x-a).\{-\frac{(x-a)}{y-b}\}}{(y-b)^2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_89.jpg) …….[From equation (1)]
…….[From equation (1)]
![Rendered by QuickLaTeX.com =-[\frac{(y-b)^2+(x-a)^2}{(y-b)^3}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_90.jpg)
![Rendered by QuickLaTeX.com [\frac{1+[\frac{dy}{dx}]^2}{\frac{d^2y}{dx^2}}]^{\frac{3}{2}}= \frac{[1+\frac{(x-a)^2}{(y-b)^2}]^{\frac{3}{2}}}{-[\frac{(y-b)^2 + (x-a)^2}{(y-b)^3}]}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_91.jpg)
=![Rendered by QuickLaTeX.com \frac{[\frac{[(y-b)^2+(x-a)^2]}{(y-b)^2}]^{\frac{3}{2}}}{-[\frac{(y-b)^2+(x-a)^2}{(y-b)^3}]}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_92.jpg)
=![Rendered by QuickLaTeX.com \frac{[\frac{c^2}{(y-b)^2}]\frac{3}{2}}{-\frac{c^2}{(y-b)^3}}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_93.jpg)
=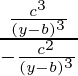
= – c, which is constant and is independent of a and b.
Hence proved.
问题16。如果cos y = x cos(a + y),且cos a≠±1,则证明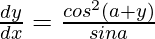
解决方案:
According to the question
cos y = x cos (a + y)
On differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d}{dx}[cos y]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_96.jpg) =
= ![Rendered by QuickLaTeX.com \frac{d}{dx}[x cos(a + y)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_97.jpg)
⇒ – sin y dy/dx = cos (a + y). 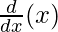 + x
+ x![Rendered by QuickLaTeX.com \frac{d}{dx}[cos (x+y)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_99.jpg)
⇒ – sin y dy/dx = cos (a + y) + x [-sin (a + y)]dy/dx
⇒ [x sin (a + y) – sin y] dy/dx = cos (a + y) ……..(1)
Since cos y = x cos (a + y), x =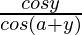
Now we can reduce eq(1)
![Rendered by QuickLaTeX.com [\frac{cosy}{cos(a+y)}.sin(a+y)-siny]\frac{dy}{dx}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_101.jpg) = cos(a + y)
= cos(a + y)
⇒ [cos y.sin (a + y)- sin y.cos (a + y)].dy/dx = cos2(a + y)
⇒ sin(a + y – y)dy/dx = cos2(a + b)
⇒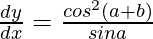
Hence proved.
问题17。如果x = a(cos t + t sin t),y = a(sin t – t cos t),则求出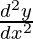
解决方案:
According to the question
x = a (cos t + t sin t) …..(1)
y = a (sin t – t cos t) …..(2)
So, \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}} …..(3)
On differentiating eq(1) w.r.t t, we get
dx/dt = a. 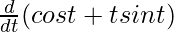
Using chain rule, we get
= a[-sin t +sin t. 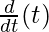 + t.
+ t.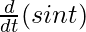 ]
]
= a [-sin t + sin t + t cos t]
= at cos t
On differentiating eq(2) w.r.t t, we get
dy/dt = a. 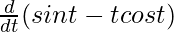
Using chain rule, we get
= a [cos t – [cost.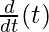 + t.
+ t.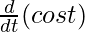 ]]
]]
= a[cos t – {cos t – t sin t}]
= at sin t
Now put the values of dx/dt and dy/dt in eq(1), we get
dy/dx = at sin t/at cos t = tan t
Again differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}= \frac{d}{dx}[\frac{dy}{dx}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_110.jpg)
= 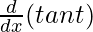
= sec 2 t.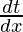
= sec2 t.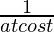 ……..[dx/dt = atcost ⇒ dt/dx = 1/atcost]
……..[dx/dt = atcost ⇒ dt/dx = 1/atcost]
= sec3t/at
问题18:如果f(x)= | x |如图3所示,证明对所有实数x都存在f”(x)并找到它。
解决方案:
As we know that |x| = 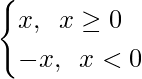
So, when x ≥ 0, f(x) = |x|3 = x3
So, on differentiating both side w.r.t x, we get
f'(x) = 3x2
Again, differentiating both side w.r.t x, we get
f”(x) = 6 x
When x < 0, f(x) = |x|3 = -x3
So, on differentiating both side w.r.t x, we get
f'(x) = – 3x2
Again, differentiating both side w.r.t x, we get
f”(x) = -6 x
So, for f(x) = |x|3, f”(x) exists for all real x, and is given by
f”(x) = 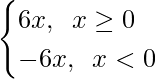
问题19:使用数学归纳法证明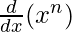 =(nx) n – 1对于所有正整数n。
=(nx) n – 1对于所有正整数n。
解决方案:
So, P(n) = 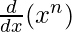 = (nx)n – 1
= (nx)n – 1
For n = 1:
P(1) : 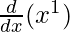 = (1x)1 – 1 =1
= (1x)1 – 1 =1
Hence, P(n) is true for n = 1
Let us considered P(k) is true for some positive integer k.
So, P(k): 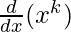 = (kx)k – 1
= (kx)k – 1
For P(k + 1): 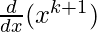 = ((k + 1)x)(k + 1) – 1
= ((k + 1)x)(k + 1) – 1
x k 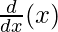 + x.
+ x.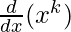 ….(Using applying product rule)
….(Using applying product rule)
= x k .1 + x . k . x k-1
= x k + k x k
= (k + 1) x k
= (k + 1) x(k + 1) – 1
Hence, P(k+1) is true whenever P(k) is true.
So, according to the principle of mathematical induction, P(n) is true for every positive integer n.
Hence proved.
问题20.使用sin(A + B)= sin A cos B + cos A sin B的事实和微分,求出余弦的和公式。
解决方案:
According to the question
sin(A + B) = sin A cos B + cos A sin B
On differentiating both sides w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d}{dx} [sin(A+B)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_123.jpg) =
= 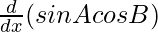 +
+ 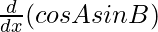
⇒ cos (A + B).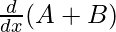 = cos B.
= cos B. 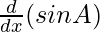 + sin A.
+ sin A. 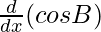 + sin B.
+ sin B.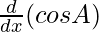 + cos A.
+ cos A. 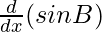
⇒ cos (A+B).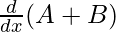 = cos B.cos A
= cos B.cos A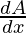 + sin A (-sin B)
+ sin A (-sin B) 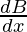 + sin B (-sin A).
+ sin B (-sin A).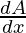 + cos A cos B
+ cos A cos B 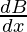
⇒ cos (A + B).![Rendered by QuickLaTeX.com [ \frac{dA}{dx}+ \frac{dB}{dx}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_136.jpg) =(cos A cos B – sin A sin B).
=(cos A cos B – sin A sin B). ![Rendered by QuickLaTeX.com [ \frac{dA}{dx}+ \frac{dB}{dx}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_137.jpg)
Hence, cos (A + B) = cos A cos B – sin A sin B
问题21.是否存在一个在任何地方都连续但不能精确地区分为两点的函数?证明你的答案。
解决方案:
Let us consider a function f given as
f(x) = |x – 1| + |x – 2|
As we already know that the modulus functions are continuous at every point
So, there sum is also continuous at every point but not differentiable at every point x = 0
Let x = 1, 2
Now at x = 1
L.H.D = lim x⇢ 1– 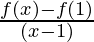
L.H.D = limh⇢0 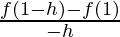
= limh⇢0 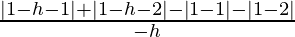
= limh⇢0 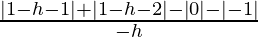
= limh⇢0 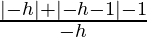
= limh⇢0 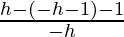
= limh⇢0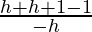
= limh⇢0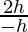
= -2
R.H.D = limx⇢1+ 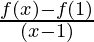
R.H.D = limh⇢0 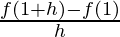
= limh⇢0 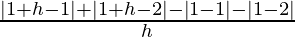
= limh⇢0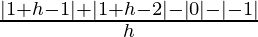
= limh⇢0 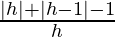
= limh⇢0 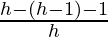
= limh⇢0 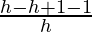
= limh⇢0 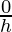
= 0
Since L.H.D ≠ R.H.D
So given function f is not differentiable at x = 1.
Similarly, we get that the given function is not differentiable at x = 2.
Hence, there exist a function which is continuous everywhere but not differentiable to exactly two points.
问题22:如果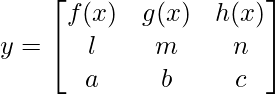 ,证明
,证明
解决方案:
Given that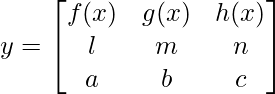
⇒ y =(mc – nb) f(x)- (lc – na )g(x) +(lb – ma) h(x)
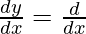 [(mc -nb) f(x)] –
[(mc -nb) f(x)] –  [(lc – na) g(x)] +
[(lc – na) g(x)] + 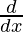 [(lb – ma) h(x)]
[(lb – ma) h(x)]
= (mc – nb) f'(x) – (lc – na) g'(x) + (lb – ma ) h’ (x)
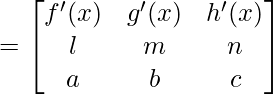
So,
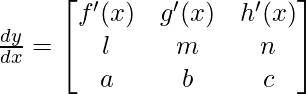
Hence proved.
问题23:如果y = 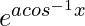 ,-1≤x≤1,表明
,-1≤x≤1,表明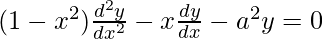
解决方案:
According to the question
y = 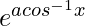
Now we are taking logarithm on both sides,
log y = a cos-1 x log e
log y = a cos -1 x
On differentiating both sides w.r.t x, we get
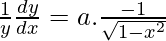
⇒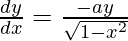
On squaring both sides,we get
![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2=\frac{a^2y^2}{1-x^2}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_167.jpg)
⇒(1-x 2)![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_168.jpg) =a 2 y 2
=a 2 y 2
On differentiating again both the side w.r.t x, we get
![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2 \frac{d}{dx}(1-x^2)+(1-x^2)\frac{d}{dx} [[\frac{dy}{dx}]^2]=a^2 \frac{d}{dx}(y^2)](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_169.jpg)
⇒![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2(-2x)+(1-x^2).2 \frac{dy}{dx}. \frac{d^2y}{dx^2}=a^2.2y \frac{dy}{dx}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_170.jpg)
⇒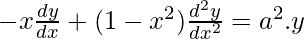
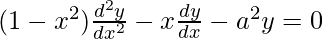
Hence proved
解决方案:
Let us assume y =![]()
Now, differentiate w.r.t x and by quotient rule, we obtain
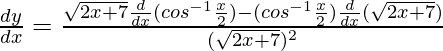
= ![Rendered by QuickLaTeX.com \frac{\sqrt{2x+7}[\frac{-1}{\sqrt{1-(\frac{x}{2})^2}}.\frac{d}{dx}(\frac{x}{2})]-(cos^{-1}\frac{x}{2})\frac{1}{2\sqrt{2x+7}}.\frac{d}{dx}(2x+7)}{2x+\frac{7}{2}}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_19.jpg)
= ![Rendered by QuickLaTeX.com \frac{\sqrt{2x+7}\frac{-1}{\sqrt{4-x^2}}-[cos^{-1}\frac{x}{2}]\frac{2}{2\sqrt{2x+7}}}{2x+7}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_20.jpg)
= 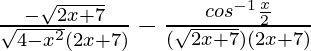
= ![Rendered by QuickLaTeX.com -[\frac{1}{\sqrt{4-x^2}\sqrt{2x+7}}+\frac{cos^{-1}\frac{x}{2}}{(2x+7)^\frac{1}{2}}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_22.jpg)
问题6。 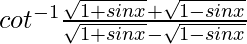 ,0
,0 π/ 2
解决方案:
Let us assume y = ![]() ……(1)
……(1)
Now solve ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= 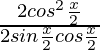
= cotx/2
Now put this value in eq(1), we get
y = cot-1(cotx/2)
y = x/2
Now, differentiate w.r.t x
![]()
dy/dx = 1/2
问题7.(log x) log x ,x> 1
解决方案:
Let us assume y = (log x)log x
Now we are taking logarithm on both sides,
log y = log x .log(log x)
Now, differentiate w.r.t x on botj side, we get
![]()
![]()
![]()
![]()
![]()
问题8.对于某些常数a和b,cos(a cos x + b sin x)。
解决方案:
Let us assume y = cos(a cos x + b sin x)
Now, differentiate w.r.t x
![]()
By using chain rule, we get
![]()
= -sin x(a cos x + b sin x).[a (-sin x) + b cos x]
= (a sin x – b cos x).sin (a cos x + b sin x)
问题9.(sin x – cos x) (sin x – cos x) , π/ 4
解决方案:
Let us assume y = (sin x – cos x)(sin x – cos x)
Now we are taking logarithm on both sides,
log y = (sin x – cos x).log(sin x – cos x)
Now, differentiate w.r.t x, we get
![]()
Using chain rule, we get
![]()
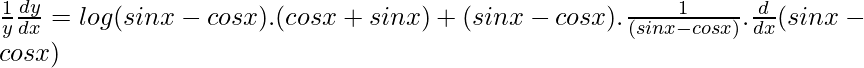
dy/dx = (sinx – cosx)(sinx – cosx)[(cosx + sinx).log(sinx – cosx) + (cosx + sinx)]
dy/dx = (sinx – cosx)(sinx – cosx)(cosx + sinx)[1 + log (sinx – cosx)]
问题10. x x + x a + a x + a对于某些固定的a> 0和x> 0
解决方案:
Let us assume y = xx + xa + ax + aa
Also, let us assume xx = u, xa = v, ax = w, aa = s
Therefore, y = u + v + w + s
So, on differentiating w.r.t x, we get
![]() ……….(1)
……….(1)
So first we solve: u = xx
Now we are taking logarithm on both sides,
log u = log xx
log u = x log x
On differentiating both sides w.r.t x, we get
![]()
![]()
du/dx = xx[logx + 1] = xx(1 + logx) …….(2)
Now we solve: v = xa
On differentiating both sides w.r.t x, we get
![]()
dv/dx = ax(a – 1) ……(3)
Now we solve: w = ax
Now we are taking logarithm on both sides,
log w =log a x
log w = x log a
On differentiating both sides w.r.t x, we get
![]()
dw/dx = w loga
dw/dx = axloga ………(4)
Now we solve: s = a a
So, on differentiating w.r.t x, we get
ds/dx = 0 ………(5)
Now put all these values from eq(2), (3), (4), (5) in eq(1), we get
dy/dx = xx(1 + logx) + ax(a – 1) + axloga + 0
= xx (1 + log x) + axa -1 + ax log a
问题11.区分wrt x, 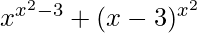 ,对于x> 3
,对于x> 3
解决方案:
Let us assume y =![]()
Also let us considered u = ![]() and v =
and v = ![]()
so, y = u + v
On differentiating both side w.r.t x, we get
![]() …….(1)
…….(1)
So, now we solve, u = ![]()
Now we are taking logarithm on both sides,
log u = log ![]()
log u = (x 2 – 3) log x
On differentiating w.r.t x, we get
![]()
![]()
=![]() …….(2)
…….(2)
Now we solve: v = ![]()
Now we are taking logarithm on both sides,
log v = ![]()
log v = x2 log(x – 3)
On differentiating both sides w.r.t x, we get
![]()
![]()
![]()
![]() …..(3)
…..(3)
Now put all these values from eq(2), and (3) in eq(1), we get
![]()
问题12.如果y = 12(1-cos t),x = 10(t-sin t),- π/ 2
解决方案:
According to the question
y = 12(1 – cos t) ……(1)
x = 10 (t – sin t) ……(2)
So, \frac{dy}{dx}= \frac{\frac{dy}{dt}}{\frac{dx}{dt}} ……(3)
On differentiating eq(1) w.r.t t, we get
![]()
= ![]()
= 12.[0 – (- sin t)]
= 12 sin t
On differentiating eq(2) w.r.t t, we get
![]()
= ![]()
= 10(1 – cos t)
Now put the value of dy/dt and dx/dt in eq(3), we get
![]()
= 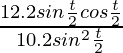
= 6/5 cot t/2
问题13查找DY / DX,如果y = -1罪X +罪-1√1-X 2,0
解决方案:
According to the question
y = sin-1 x + sin-1√1 – x2
On differentiating w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{d}{dx}[sin^{-1}x+sin ^{-1}\sqrt{1-x^2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_70.jpg)
Using chain rule, we get
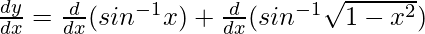
= 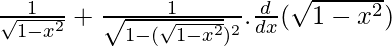
= 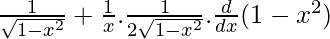
= 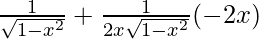
= 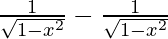
dy/dx = 0
问题14.如果x√1+ y +y√1+ x = 0,则-1
解决方案:
According to the question
x√1 + y = -y√1 + x
On squaring both sides, we get
x2 (1 + y) = y2 (1 + x)
⇒ x2 + x2 y = y2 + x y2
⇒ x2 – y2 = xy 2 – x2 y
⇒ x2 – y2 = xy (y – x)
⇒ (x + y)(x – y) = xy (y – x)
⇒ x + y = -xy
⇒ (1 + x) y = -x
⇒ y = -x/(1 + x)
On differentiating both sides w.r.t x, we get
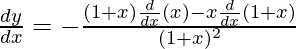
= 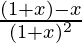
= 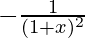
Hence proved.
问题15。如果(x – a) 2 +(y – b) 2 = c 2 ,则对于某些c> 0,证明![由QuickLaTeX.com渲染 \frac{[1+(\frac{dy}{dx})^2]^\frac{3}{2}} {\frac{d^2y}{dx^2}}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_80.jpg) 是一个独立于a和b的常数。
是一个独立于a和b的常数。
解决方案:
According to the question
(x – a)2+ (y – b)2= c2
On differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d}{dx}[(x-a)^2]+\frac{d}{dx}[(y-b)^2]=\frac{d}{dx}(c^2)](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_81.jpg)
⇒ 2(x – a).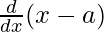 + 2(y – b)
+ 2(y – b)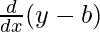 = 0
= 0
⇒ 2(x – a).1 + 2(y – b).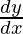 = 0
= 0
⇒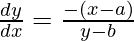 …….(1)
…….(1)
Again on differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2} = \frac{d}{dx}[\frac{-(x-a)}{y-b}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_86.jpg)
![Rendered by QuickLaTeX.com = -[\frac{(y-b).\frac{d}{dx}(x-a)-(x-a).\frac{d}{dx}(y-b)}{(y-b)^2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_87.jpg)
![Rendered by QuickLaTeX.com =-[\frac{(y-b)-(x-a).\frac{dy}{dx}}{(y-b)^2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_88.jpg)
![Rendered by QuickLaTeX.com = -[\frac{(y-b)-(x-a).\{-\frac{(x-a)}{y-b}\}}{(y-b)^2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_89.jpg) …….[From equation (1)]
…….[From equation (1)]
![Rendered by QuickLaTeX.com =-[\frac{(y-b)^2+(x-a)^2}{(y-b)^3}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_90.jpg)
![Rendered by QuickLaTeX.com [\frac{1+[\frac{dy}{dx}]^2}{\frac{d^2y}{dx^2}}]^{\frac{3}{2}}= \frac{[1+\frac{(x-a)^2}{(y-b)^2}]^{\frac{3}{2}}}{-[\frac{(y-b)^2 + (x-a)^2}{(y-b)^3}]}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_91.jpg)
=![Rendered by QuickLaTeX.com \frac{[\frac{[(y-b)^2+(x-a)^2]}{(y-b)^2}]^{\frac{3}{2}}}{-[\frac{(y-b)^2+(x-a)^2}{(y-b)^3}]}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_92.jpg)
=![Rendered by QuickLaTeX.com \frac{[\frac{c^2}{(y-b)^2}]\frac{3}{2}}{-\frac{c^2}{(y-b)^3}}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_93.jpg)
=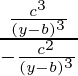
= – c, which is constant and is independent of a and b.
Hence proved.
问题16。如果cos y = x cos(a + y),且cos a≠±1,则证明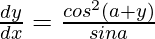
解决方案:
According to the question
cos y = x cos (a + y)
On differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d}{dx}[cos y]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_96.jpg) =
= ![Rendered by QuickLaTeX.com \frac{d}{dx}[x cos(a + y)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_97.jpg)
⇒ – sin y dy/dx = cos (a + y). 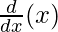 + x
+ x![Rendered by QuickLaTeX.com \frac{d}{dx}[cos (x+y)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_99.jpg)
⇒ – sin y dy/dx = cos (a + y) + x [-sin (a + y)]dy/dx
⇒ [x sin (a + y) – sin y] dy/dx = cos (a + y) ……..(1)
Since cos y = x cos (a + y), x =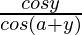
Now we can reduce eq(1)
![Rendered by QuickLaTeX.com [\frac{cosy}{cos(a+y)}.sin(a+y)-siny]\frac{dy}{dx}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_101.jpg) = cos(a + y)
= cos(a + y)
⇒ [cos y.sin (a + y)- sin y.cos (a + y)].dy/dx = cos2(a + y)
⇒ sin(a + y – y)dy/dx = cos2(a + b)
⇒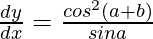
Hence proved.
问题17。如果x = a(cos t + t sin t),y = a(sin t – t cos t),则求出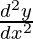
解决方案:
According to the question
x = a (cos t + t sin t) …..(1)
y = a (sin t – t cos t) …..(2)
So, \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}} …..(3)
On differentiating eq(1) w.r.t t, we get
dx/dt = a. 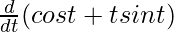
Using chain rule, we get
= a[-sin t +sin t. 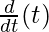 + t.
+ t.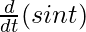 ]
]
= a [-sin t + sin t + t cos t]
= at cos t
On differentiating eq(2) w.r.t t, we get
dy/dt = a. 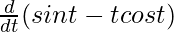
Using chain rule, we get
= a [cos t – [cost.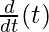 + t.
+ t.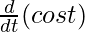 ]]
]]
= a[cos t – {cos t – t sin t}]
= at sin t
Now put the values of dx/dt and dy/dt in eq(1), we get
dy/dx = at sin t/at cos t = tan t
Again differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}= \frac{d}{dx}[\frac{dy}{dx}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_110.jpg)
= 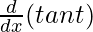
= sec 2 t.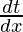
= sec2 t.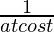 ……..[dx/dt = atcost ⇒ dt/dx = 1/atcost]
……..[dx/dt = atcost ⇒ dt/dx = 1/atcost]
= sec3t/at
问题18:如果f(x)= | x |如图3所示,证明对所有实数x都存在f”(x)并找到它。
解决方案:
As we know that |x| = 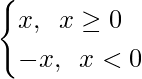
So, when x ≥ 0, f(x) = |x|3 = x3
So, on differentiating both side w.r.t x, we get
f'(x) = 3x2
Again, differentiating both side w.r.t x, we get
f”(x) = 6 x
When x < 0, f(x) = |x|3 = -x3
So, on differentiating both side w.r.t x, we get
f'(x) = – 3x2
Again, differentiating both side w.r.t x, we get
f”(x) = -6 x
So, for f(x) = |x|3, f”(x) exists for all real x, and is given by
f”(x) = 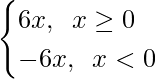
问题19:使用数学归纳法证明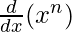 =(nx) n – 1对于所有正整数n。
=(nx) n – 1对于所有正整数n。
解决方案:
So, P(n) = 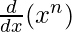 = (nx)n – 1
= (nx)n – 1
For n = 1:
P(1) : 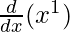 = (1x)1 – 1 =1
= (1x)1 – 1 =1
Hence, P(n) is true for n = 1
Let us considered P(k) is true for some positive integer k.
So, P(k): 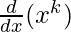 = (kx)k – 1
= (kx)k – 1
For P(k + 1): 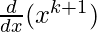 = ((k + 1)x)(k + 1) – 1
= ((k + 1)x)(k + 1) – 1
x k 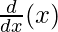 + x.
+ x.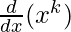 ….(Using applying product rule)
….(Using applying product rule)
= x k .1 + x . k . x k-1
= x k + k x k
= (k + 1) x k
= (k + 1) x(k + 1) – 1
Hence, P(k+1) is true whenever P(k) is true.
So, according to the principle of mathematical induction, P(n) is true for every positive integer n.
Hence proved.
问题20.使用sin(A + B)= sin A cos B + cos A sin B的事实和微分,求出余弦的和公式。
解决方案:
According to the question
sin(A + B) = sin A cos B + cos A sin B
On differentiating both sides w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d}{dx} [sin(A+B)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_123.jpg) =
= 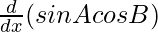 +
+ 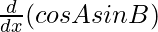
⇒ cos (A + B).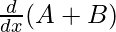 = cos B.
= cos B. 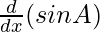 + sin A.
+ sin A. 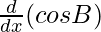 + sin B.
+ sin B.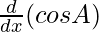 + cos A.
+ cos A. 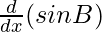
⇒ cos (A+B).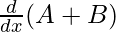 = cos B.cos A
= cos B.cos A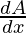 + sin A (-sin B)
+ sin A (-sin B) 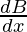 + sin B (-sin A).
+ sin B (-sin A).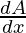 + cos A cos B
+ cos A cos B 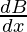
⇒ cos (A + B).![Rendered by QuickLaTeX.com [ \frac{dA}{dx}+ \frac{dB}{dx}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_136.jpg) =(cos A cos B – sin A sin B).
=(cos A cos B – sin A sin B). ![Rendered by QuickLaTeX.com [ \frac{dA}{dx}+ \frac{dB}{dx}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_137.jpg)
Hence, cos (A + B) = cos A cos B – sin A sin B
问题21.是否存在一个在任何地方都连续但不能精确地区分为两点的函数?证明你的答案。
解决方案:
Let us consider a function f given as
f(x) = |x – 1| + |x – 2|
As we already know that the modulus functions are continuous at every point
So, there sum is also continuous at every point but not differentiable at every point x = 0
Let x = 1, 2
Now at x = 1
L.H.D = lim x⇢ 1– 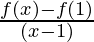
L.H.D = limh⇢0 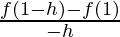
= limh⇢0 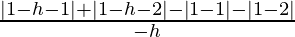
= limh⇢0 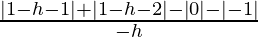
= limh⇢0 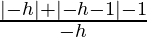
= limh⇢0 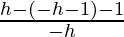
= limh⇢0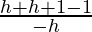
= limh⇢0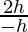
= -2
R.H.D = limx⇢1+ 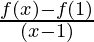
R.H.D = limh⇢0 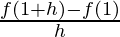
= limh⇢0 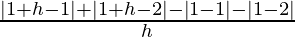
= limh⇢0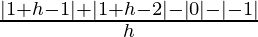
= limh⇢0 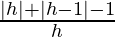
= limh⇢0 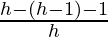
= limh⇢0 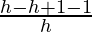
= limh⇢0 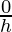
= 0
Since L.H.D ≠ R.H.D
So given function f is not differentiable at x = 1.
Similarly, we get that the given function is not differentiable at x = 2.
Hence, there exist a function which is continuous everywhere but not differentiable to exactly two points.
问题22:如果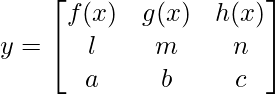 ,证明
,证明
解决方案:
Given that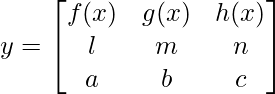
⇒ y =(mc – nb) f(x)- (lc – na )g(x) +(lb – ma) h(x)
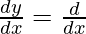 [(mc -nb) f(x)] –
[(mc -nb) f(x)] –  [(lc – na) g(x)] +
[(lc – na) g(x)] + 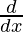 [(lb – ma) h(x)]
[(lb – ma) h(x)]
= (mc – nb) f'(x) – (lc – na) g'(x) + (lb – ma ) h’ (x)
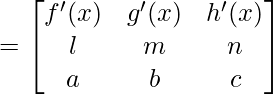
So,
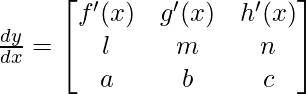
Hence proved.
问题23:如果y = 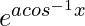 ,-1≤x≤1,表明
,-1≤x≤1,表明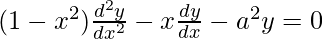
解决方案:
According to the question
y = 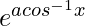
Now we are taking logarithm on both sides,
log y = a cos-1 x log e
log y = a cos -1 x
On differentiating both sides w.r.t x, we get
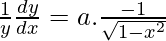
⇒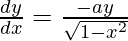
On squaring both sides,we get
![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2=\frac{a^2y^2}{1-x^2}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_167.jpg)
⇒(1-x 2)![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_168.jpg) =a 2 y 2
=a 2 y 2
On differentiating again both the side w.r.t x, we get
![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2 \frac{d}{dx}(1-x^2)+(1-x^2)\frac{d}{dx} [[\frac{dy}{dx}]^2]=a^2 \frac{d}{dx}(y^2)](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_169.jpg)
⇒![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2(-2x)+(1-x^2).2 \frac{dy}{dx}. \frac{d^2y}{dx^2}=a^2.2y \frac{dy}{dx}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_170.jpg)
⇒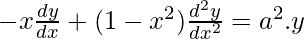
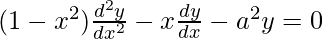
Hence proved
解决方案:
According to the question
y = sin-1 x + sin-1√1 – x2
On differentiating w.r.t x, we get
![]()
Using chain rule, we get
![]()
= ![]()
= ![]()
= ![]()
= ![]()
dy/dx = 0
问题14.如果x√1+ y +y√1+ x = 0,则-1
解决方案:
According to the question
x√1 + y = -y√1 + x
On squaring both sides, we get
x2 (1 + y) = y2 (1 + x)
⇒ x2 + x2 y = y2 + x y2
⇒ x2 – y2 = xy 2 – x2 y
⇒ x2 – y2 = xy (y – x)
⇒ (x + y)(x – y) = xy (y – x)
⇒ x + y = -xy
⇒ (1 + x) y = -x
⇒ y = -x/(1 + x)
On differentiating both sides w.r.t x, we get
![]()
= ![]()
= ![]()
Hence proved.
问题15。如果(x – a) 2 +(y – b) 2 = c 2 ,则对于某些c> 0,证明![由QuickLaTeX.com渲染 \frac{[1+(\frac{dy}{dx})^2]^\frac{3}{2}} {\frac{d^2y}{dx^2}}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_80.jpg) 是一个独立于a和b的常数。
是一个独立于a和b的常数。
解决方案:
According to the question
(x – a)2+ (y – b)2= c2
On differentiating both side w.r.t x, we get
![]()
⇒ 2(x – a).![]() + 2(y – b)
+ 2(y – b)![]() = 0
= 0
⇒ 2(x – a).1 + 2(y – b).![]() = 0
= 0
⇒![]() …….(1)
…….(1)
Again on differentiating both side w.r.t x, we get
![]()
![]()
![Rendered by QuickLaTeX.com =-[\frac{(y-b)-(x-a).\frac{dy}{dx}}{(y-b)^2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_88.jpg)
![Rendered by QuickLaTeX.com = -[\frac{(y-b)-(x-a).\{-\frac{(x-a)}{y-b}\}}{(y-b)^2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_89.jpg) …….[From equation (1)]
…….[From equation (1)]
![]()
![Rendered by QuickLaTeX.com [\frac{1+[\frac{dy}{dx}]^2}{\frac{d^2y}{dx^2}}]^{\frac{3}{2}}= \frac{[1+\frac{(x-a)^2}{(y-b)^2}]^{\frac{3}{2}}}{-[\frac{(y-b)^2 + (x-a)^2}{(y-b)^3}]}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_91.jpg)
=![Rendered by QuickLaTeX.com \frac{[\frac{[(y-b)^2+(x-a)^2]}{(y-b)^2}]^{\frac{3}{2}}}{-[\frac{(y-b)^2+(x-a)^2}{(y-b)^3}]}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_92.jpg)
=![Rendered by QuickLaTeX.com \frac{[\frac{c^2}{(y-b)^2}]\frac{3}{2}}{-\frac{c^2}{(y-b)^3}}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions-%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%205%20Continuity%20And%20Differentiability%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%205_93.jpg)
=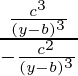
= – c, which is constant and is independent of a and b.
Hence proved.
问题16。如果cos y = x cos(a + y),且cos a≠±1,则证明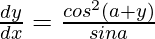
解决方案:
According to the question
cos y = x cos (a + y)
On differentiating both side w.r.t x, we get
![]() =
= ![]()
⇒ – sin y dy/dx = cos (a + y). ![]() + x
+ x![]()
⇒ – sin y dy/dx = cos (a + y) + x [-sin (a + y)]dy/dx
⇒ [x sin (a + y) – sin y] dy/dx = cos (a + y) ……..(1)
Since cos y = x cos (a + y), x =![]()
Now we can reduce eq(1)
![]() = cos(a + y)
= cos(a + y)
⇒ [cos y.sin (a + y)- sin y.cos (a + y)].dy/dx = cos2(a + y)
⇒ sin(a + y – y)dy/dx = cos2(a + b)
⇒![]()
Hence proved.
问题17。如果x = a(cos t + t sin t),y = a(sin t – t cos t),则求出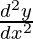
解决方案:
According to the question
x = a (cos t + t sin t) …..(1)
y = a (sin t – t cos t) …..(2)
So, \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}} …..(3)
On differentiating eq(1) w.r.t t, we get
dx/dt = a. ![]()
Using chain rule, we get
= a[-sin t +sin t. ![]() + t.
+ t.![]() ]
]
= a [-sin t + sin t + t cos t]
= at cos t
On differentiating eq(2) w.r.t t, we get
dy/dt = a. ![]()
Using chain rule, we get
= a [cos t – [cost.![]() + t.
+ t.![]() ]]
]]
= a[cos t – {cos t – t sin t}]
= at sin t
Now put the values of dx/dt and dy/dt in eq(1), we get
dy/dx = at sin t/at cos t = tan t
Again differentiating both side w.r.t x, we get
![]()
= ![]()
= sec 2 t.![]()
= sec2 t.![]() ……..[dx/dt = atcost ⇒ dt/dx = 1/atcost]
……..[dx/dt = atcost ⇒ dt/dx = 1/atcost]
= sec3t/at
问题18:如果f(x)= | x |如图3所示,证明对所有实数x都存在f”(x)并找到它。
解决方案:
As we know that |x| = 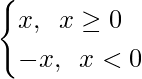
So, when x ≥ 0, f(x) = |x|3 = x3
So, on differentiating both side w.r.t x, we get
f'(x) = 3x2
Again, differentiating both side w.r.t x, we get
f”(x) = 6 x
When x < 0, f(x) = |x|3 = -x3
So, on differentiating both side w.r.t x, we get
f'(x) = – 3x2
Again, differentiating both side w.r.t x, we get
f”(x) = -6 x
So, for f(x) = |x|3, f”(x) exists for all real x, and is given by
f”(x) = 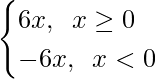
问题19:使用数学归纳法证明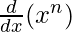 =(nx) n – 1对于所有正整数n。
=(nx) n – 1对于所有正整数n。
解决方案:
So, P(n) = ![]() = (nx)n – 1
= (nx)n – 1
For n = 1:
P(1) : ![]() = (1x)1 – 1 =1
= (1x)1 – 1 =1
Hence, P(n) is true for n = 1
Let us considered P(k) is true for some positive integer k.
So, P(k): ![]() = (kx)k – 1
= (kx)k – 1
For P(k + 1): ![]() = ((k + 1)x)(k + 1) – 1
= ((k + 1)x)(k + 1) – 1
x k ![]() + x.
+ x.![]() ….(Using applying product rule)
….(Using applying product rule)
= x k .1 + x . k . x k-1
= x k + k x k
= (k + 1) x k
= (k + 1) x(k + 1) – 1
Hence, P(k+1) is true whenever P(k) is true.
So, according to the principle of mathematical induction, P(n) is true for every positive integer n.
Hence proved.
问题20.使用sin(A + B)= sin A cos B + cos A sin B的事实和微分,求出余弦的和公式。
解决方案:
According to the question
sin(A + B) = sin A cos B + cos A sin B
On differentiating both sides w.r.t x, we get
![]() =
= ![]() +
+ ![]()
⇒ cos (A + B).![]() = cos B.
= cos B. ![]() + sin A.
+ sin A. ![]() + sin B.
+ sin B.![]() + cos A.
+ cos A. ![]()
⇒ cos (A+B).![]() = cos B.cos A
= cos B.cos A![]() + sin A (-sin B)
+ sin A (-sin B) ![]() + sin B (-sin A).
+ sin B (-sin A).![]() + cos A cos B
+ cos A cos B ![]()
⇒ cos (A + B).![]() =(cos A cos B – sin A sin B).
=(cos A cos B – sin A sin B). ![]()
Hence, cos (A + B) = cos A cos B – sin A sin B
问题21.是否存在一个在任何地方都连续但不能精确地区分为两点的函数?证明你的答案。
解决方案:
Let us consider a function f given as
f(x) = |x – 1| + |x – 2|
As we already know that the modulus functions are continuous at every point
So, there sum is also continuous at every point but not differentiable at every point x = 0
Let x = 1, 2
Now at x = 1
L.H.D = lim x⇢ 1– ![]()
L.H.D = limh⇢0 ![]()
= limh⇢0 ![]()
= limh⇢0 ![]()
= limh⇢0 ![]()
= limh⇢0 ![]()
= limh⇢0![]()
= limh⇢0![]()
= -2
R.H.D = limx⇢1+ ![]()
R.H.D = limh⇢0 ![]()
= limh⇢0 ![]()
= limh⇢0![]()
= limh⇢0 ![]()
= limh⇢0 ![]()
= limh⇢0 ![]()
= limh⇢0 ![]()
= 0
Since L.H.D ≠ R.H.D
So given function f is not differentiable at x = 1.
Similarly, we get that the given function is not differentiable at x = 2.
Hence, there exist a function which is continuous everywhere but not differentiable to exactly two points.
问题22:如果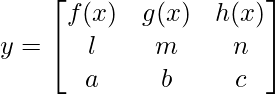 ,证明
,证明
解决方案:
Given that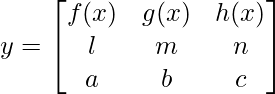
⇒ y =(mc – nb) f(x)- (lc – na )g(x) +(lb – ma) h(x)
![]() [(mc -nb) f(x)] –
[(mc -nb) f(x)] – ![]() [(lc – na) g(x)] +
[(lc – na) g(x)] + ![]() [(lb – ma) h(x)]
[(lb – ma) h(x)]
= (mc – nb) f'(x) – (lc – na) g'(x) + (lb – ma ) h’ (x)
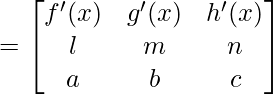
So,
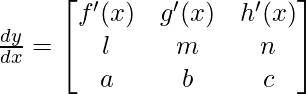
Hence proved.
问题23:如果y = 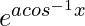 ,-1≤x≤1,表明
,-1≤x≤1,表明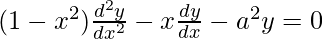
解决方案:
According to the question
y = ![]()
Now we are taking logarithm on both sides,
log y = a cos-1 x log e
log y = a cos -1 x
On differentiating both sides w.r.t x, we get
![]()
⇒![]()
On squaring both sides,we get
![]()
⇒(1-x 2)![]() =a 2 y 2
=a 2 y 2
On differentiating again both the side w.r.t x, we get
![]()
⇒![]()
⇒![]()
![]()
Hence proved