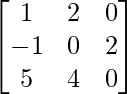问题1(i):计算以下总和: 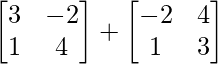 。
。
解决方案:
As the matrices are of the same dimensions, we can add them to get a matrix of the same dimensions which is 2×2.
=>
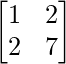
=>
问题1(ii):计算以下总和:  。
。
解决方案:
As the matrices are of the same dimensions, we can add them to get a matrix of the same dimensions which is 3×3.
=>
=>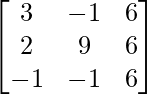
问题2:让A = 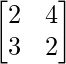 ,B =
,B = 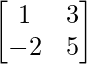 和C =
和C = 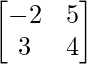 。查找以下每个:
。查找以下每个:
(i):2A – 3B
解决方案:
Both the matrices A and B are of the same order which is 2×2, hence the operation can be performed.
=> 2A =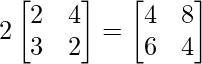
=> 3B =
=> 2A – 3B =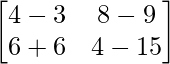
=> 2A – 3B =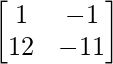
(ii):B – 4C
解决方案:
Both the matrices B and C are of the same order which is 2×2, hence the operation can be performed.
=> B =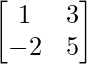
=> 4C =
=> B – 4C =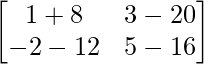
=> B – 4C =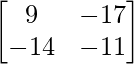
(iii):3A – C
解决方案:
Both the matrices A and C are of the same order which is 2×2, hence the operation can be performed.
=> 3A =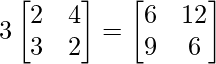
=> C =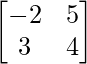
=> 3A – C =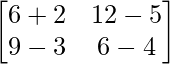
=> 3A – C =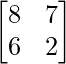
(iv):3A -2B + 3C
解决方案:
The matrices A, B and C are of the same order which is 2×2, hence the operation can be performed.
=> 3A =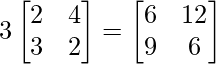
=> 2B =
=> 3C =
=> 3A – 2B + 3C =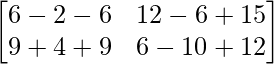
=> 3A – 2B + 3C =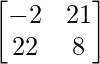
问题3:如果A = 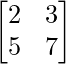 ,B =
,B =  ,C =
,C =  , 找:
, 找:
(i):A + B和B + C
解决方案:
A and B can not be added since A’s order is 2×2 which is different from B’s order which is 2×3.
B+C can be computed and is solved as follows:
=> B + C =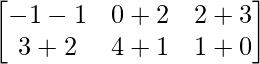
=> B + C =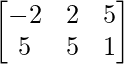
(ii):2B + 3A和3C – 4B
解决方案:
A and B can not be added since A’s order is 2×2 which is different from B’s order which is 2×3, and thus 2B + 3A can not be calculated.
3C – 4B can be computed and is solved as follows:
=> 3C =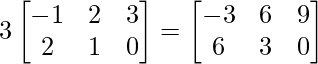
=> 4B =
=> 3C – 4B =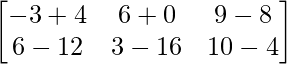
=> 3C – 4B =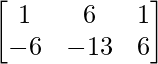
问题4:设A = 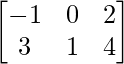 ,B =
,B = 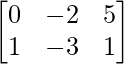 和C =
和C =  。计算2A – 3B + 4C。
。计算2A – 3B + 4C。
解决方案:
The result can be computed since A, B and C are of the same order which is 2×3.
=> 2A =
=> 3B =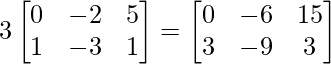
=> 4C =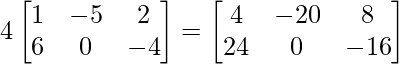
=> 2A – 3B + 4C =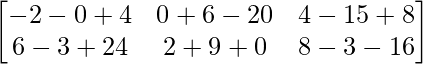
=> 2A – 3B + 4C =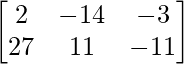
问题5:如果A = diag(2,-5,9),B = diag(1,1,-4)和C = diag(-6,3,4),则找到:
(i):A – 2B
解决方案:
In the given question A and B are diagonal matrices of the order 3×3, thus the only non-zero elements are present in the diagonal.
=> A = diag(2, -5, 9)
=> 2B = 2. diag(1, 1, -4) = diag(2, 2, -8)
=> A – 2B = diag(2-2, -5-2, 9+8)
=> A – 2B = diag(0, -7, 17)
(ii):B + C – 2A
解决方案:
In the given question A, B and C are diagonal matrices of the order 3×3, thus the only non-zero elements are present in the diagonal.
=> B = diag(1, 1, -4)
=> C = diag(-6, 3, 4)
=> 2A = 2. diag(2, -5, 9) = diag(4, -10, 18)
=> B + C – 2A = diag(1-6-4, 1+3+10, -4+4-18)
=> B + C – 2A = diag(-9, 14, -18)
(iii):2A + 3B – 5C
解决方案:
In the given question A, B and C are diagonal matrices of the order 3×3, thus the only non-zero elements are present in the diagonal.
=> 2A = 2. diag(2, -5, 9) = diag(4, -10, 18)
=> 3B = 3. diag(1, 1, -4) = diag(3, 3, -12)
=> 5C = 5. diag(-6, 3, 4) = diag(-30, 15, 20)
=> 2A + 3B – 5C = diag(4+3+30, -10+3-15, 18-12-20)
=> 2A + 3B – 5C = diag(37, -22, -14)
问题6:给定矩阵A =  ,B =
,B =  和C =
和C = 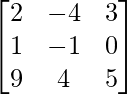 。验证(A + B)+ C = A +(B + C)。
。验证(A + B)+ C = A +(B + C)。
解决方案:
Given L.H.S :
=> (A + B) = 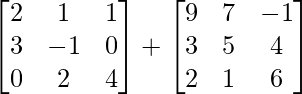
=> (A + B) =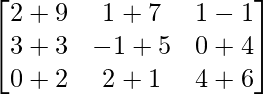
=> (A + B) =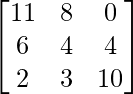
=> (A + B) + C =
=> (A + B) + C =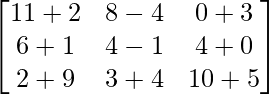
=> (A + B) + C =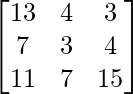
Given R.H.S :
=> (B + C) =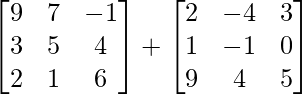
=> (B + C) =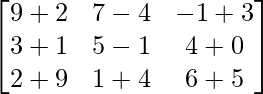
=> (B + C) =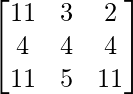
=> A + (B + C) =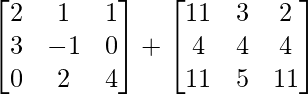
=> A + (B + C) =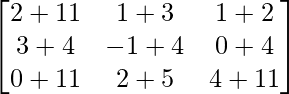
=> A + (B + C) =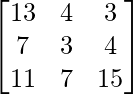
Hence R.H.S = L.H.S has been verified.
问题7:如果X + Y =,则求矩阵X和Y 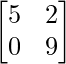 和X – Y =
和X – Y =  。
。
解决方案:
We know that (X + Y) + (X – Y) = 2X.
=> (X + Y) + (X – Y) =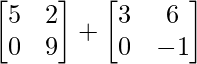
=> 2X =
=> 2X =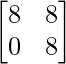
=> X =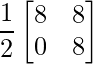
=> X =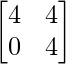
Now Y = (X + Y) – X
=> Y =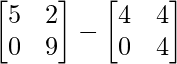
=> Y =
=> Y =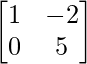
问题8:如果Y =,则找到X  和2X + Y =
和2X + Y = 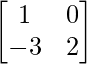 。
。
解决方案:
Given 2X + Y =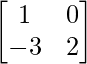
=> 2X + =
=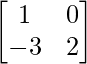
=> 2X =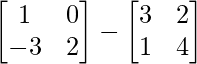
=> 2X =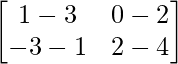
=> 2X =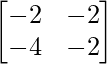
=> X =
=> X =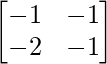
问题9:如果2X – Y =,则求矩阵X和Y 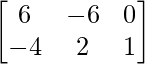 和X + 2Y =
和X + 2Y = 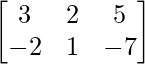 。
。
解决方案:
We know that 2 (2X – Y) + (X + 2Y) = 4X – 2Y + X + 2Y = 5X .
=> 2 (2X – Y) =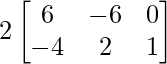
=> 2 (2X -Y) =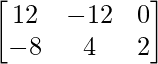
=> 2 (2X – Y) + (X + 2Y) =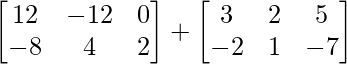
=> 5X =
=> 5X =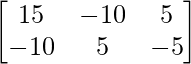
=> X =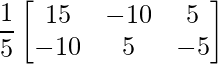
=> X =
As (X + 2Y) =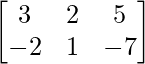
=>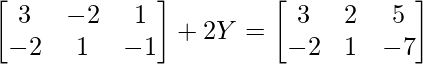
=> 2Y =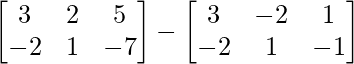
=> 2Y =
=> Y =
=> Y =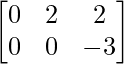
问题10:如果X – Y = 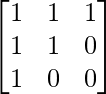 和X + Y =
和X + Y = 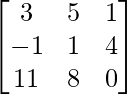 ,找到X和Y。
,找到X和Y。
解决方案:
We know that (X + Y) + (X – Y) = 2X.
=> 2X =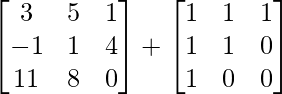
=> 2X =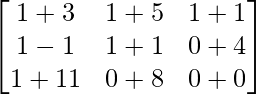
=> 2X =
=> X =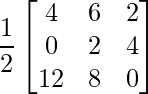
=> X =
Also (X + Y) – (X -Y) = 2Y.
=> 2Y =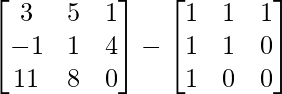
=> 2Y =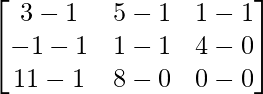
=> 2Y =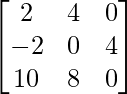
=> Y =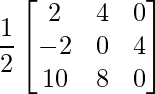
=> Y =