问题1:可以包围一个实体的最少平面数是多少?实体的名称是什么?
解决方案:
The least number of planes that are required to enclose a solid is 4.
The name of the solid is tetrahedron. It is a solid with four planes.
问题2:多面体可以有脸吗?
(i)3个三角形?
解决方案:
No, because we need minimum 4 triangular faces in order to complete a polyhedron.
(ii)4个三角形?
解决方案:
Yes, A tetrahedron has 4 triangles as its faces.
(iii)一个正方形和四个三角形?
解决方案:
Yes, A square pyramid has a square and four triangles as its faces.
问题3:是否可以使用具有给定数量的面的多面体?
解决方案:
Yes, if the number of faces is equal to or more than 4. As there is no possible polyhedron with 3 or less faces.
问题4:方棱镜和立方体相同吗?
解决方案:
Yes, a square prism is same as a cube. Both of them have 6 faces, 8 vertices and 12 edge.
The only difference is that a square prism is a 3-d shape with six rectangular shaped sides, out of which two are squares and
a cube is a rectangular prism having same length, width and height.
问题5:多面体可以有10个面,20个边和15个顶点吗?
解决方案:
No.
Reason –
Given,
Number of faces (F) = 10
Number of edges (E) = 20
Number of vertices (V) = 15
We know that, every polyhedron satisfies Euler’s formuala.
So, By using Euler’s formula –
V + F = E + 2
15 + 10 = 20 + 2
25 ≠ 22
Since, the given polyhedron does not satisfy Euler’s formula. Thus, a polyhedron can not have 10 faces, 20 edges and 15 vertices.
问题6:为以下每个多面体验证Euler公式:
(一世)
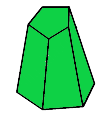
解决方案:
In the given polyhedron –
Number of faces (F) = 7
Number of edges (E) = 15
Number of vertices (V) = 10
Now, By using Euler’s formula –
V + F = E + 2
10 + 7 = 15 + 2
17 = 17
Here, Euler’s formula is satisfied.
Hence, verified.
(ii)
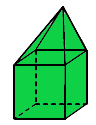
解决方案:
In the given polyhedron –
Number of faces (F) = 9
Number of edges (E) = 16
Number of vertices (V) = 9
Now, By using Euler’s formula –
V + F = E + 2
9 + 9 = 16 + 2
18 = 18
Here, Euler’s formula is satisfied.
Hence, verified.
(iii)
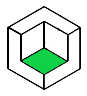
(三)
解决方案:
In the given polyhedron –
Number of faces (F) = 9
Number of edges (E) = 21
Number of vertices (V) = 14
Now, By using Euler’s formula –
V + F = E + 2
14 + 9 = 21 + 2
23 = 23
Here, Euler’s formula is satisfied.
Hence, verified.
(iv)

(四)
解决方案:
In the given polyhedron –
Number of faces (F) = 8
Number of edges (E) = 12
Number of vertices (V) = 6
Now, By using Euler’s formula –
V + F = E + 2
6 + 8 = 12 + 2
14 = 14
Here, Euler’s formula is satisfied.
Hence, verified.
(v)

(五)
解决方案:
In the given polyhedron –
Number of faces (F) = 9
Number of edges (E) = 16
Number of vertices (V) = 9
Now, By using Euler’s formula –
V + F = E + 2
9 + 9 = 16 + 2
18 = 18
Here, Euler’s formula is satisfied.
Hence, verified.
问题7:使用欧拉公式可找出未知数:
| Faces | ? | 5 | 20 |
| Vertices | 6 | ? | 12 |
| Edges | 12 | 9 | ? |
解决方案:
(i) Given,
Number of vertices (V) = 6
Number of edges (E) = 12
By using Euler’s formula –
V + F = E + 2
6 + F = 12 + 2
F = 14 – 6
F = 8
Thus, the number of faces is 8.
(ii) Given,
Number of faces (F) = 5
Number of edges (E) = 9
By using Euler’s formula –
V + F = E + 2
V + 5 = 9 + 2
V = 11 – 5
V = 6
Thus, the number of vertices is 6.
(iii) Given,
Number of vertices (V) = 12
Number of faces (F) = 20
By using Euler’s formula –
V + F = E + 2
12 + 20 = E + 2
E = 32 – 2
E = 30
Thus, the number of edges is 30.