第 10 类 RD Sharma 解决方案 - 第 10 章圆圈 - 练习 10.2 |设置 1
问题 1. 如果 PT 在 T 处与圆心为 O 且 OP = 17 cm 的圆相切,则 OT = 8 cm。求切线段 PT 的长度。
解决方案:
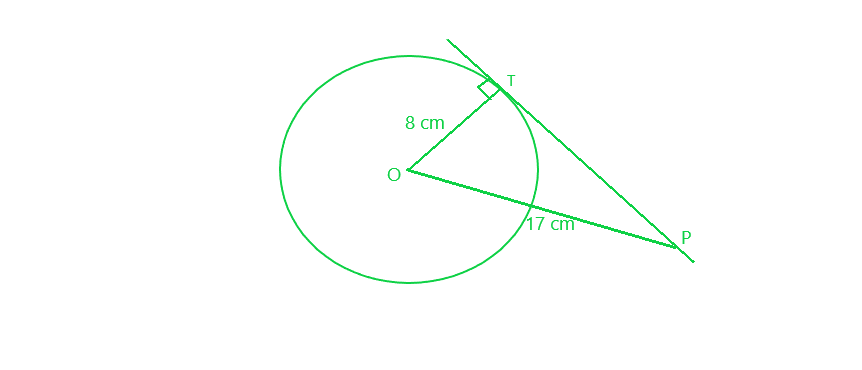
PT is the tangent to the circle with centre O, at T
=> PT⊥ OT
Radius OT = 8 cm
OP = 17 cm
Therefore, In right ∆OPT, by applying Pythagoras Theorem:
OP² = OT² + PT²
=> (17)² = (8)² + PT²
=> 289 = 64 + PT²
=> PT² = 289 – 64 = 225 = (15)²
PT = 15 cm
问题 2. 从距圆心 13 cm 的点算出半径为 5 cm 的圆的切线长度。
解决方案:

From a point P outside the circle with centre O, let us draw a tangent PT to the circle
OA = 5 cm (radius)
OB = 13 cm
OA ⊥ BA
Therefore, In right ∆OPT, by applying Pythagoras Theorem
OB² = OA² + BA²
(13)² = (5)² + BA²
=> 169 = 25 + BA²
=> BA² = 169 – 25 = 144 = (12)²
BA = 12 cm
问题 3. 点 P 距圆心 O 26 厘米,从 P 到圆的切线长度 PT 为 10 厘米。求圆的半径。
解决方案:

From a point P outside the circle with centre O, let us draw a tangent PT to the circle of radius OT
OP = 26 cm
PT = 10 cm
Therefore, In right ∆OPT, by applying Pythagoras Theorem:
OP² = OT² + PT²
=> (26)² = OT² + (10)²
=> 676 = OT² + 100
=> 676 – 100 = OT²
=> OT² = 576 = (24)²
Hence, radius of the circle = 24 cm
问题 4. 如果从两个相交的圆的公弦上的任何一点画出两个圆的切线,证明它们相等。
解决方案:

Given:
QR is the common chord of two circles intersecting each other at Q and R
A is a point on RQ when produced.
From A, AB and AC two tangents are drawn to the circles with centres O and O’ respectively.
To prove : AB = AC
Proof: AB is the tangent and AQR is the secant to the circle with centre O
=> AB² = AQ x AR (1)
Similarly, AC is the tangent and AQR is the secant to the circle with centre O’
=> AC² = AQ x AR (2)
From (1) and (2)
AB² = AC²
AB = AC
Hence, proved.
问题 5. 如果一个四边形的边与一个圆相接触,证明一对对边之和等于另一对边之和。
解决方案:
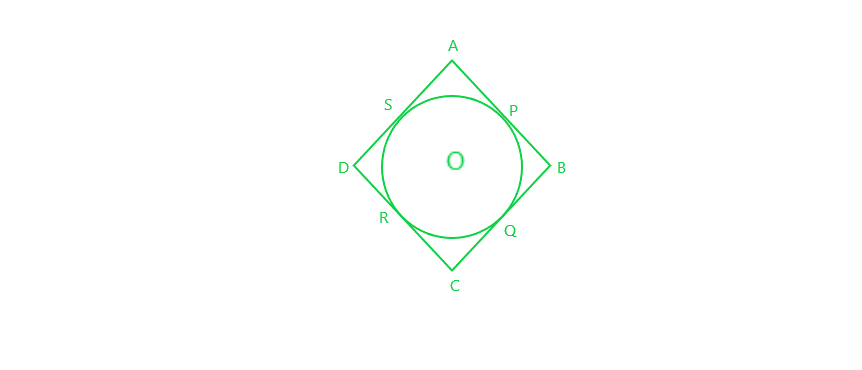
Given: The sides of a quadrilateral ABCD touch the circle at P, Q, R and S respectively
To prove : AB + CD = AP + BC
Proof : AP and AS are the tangents to the circle from A
=> AP = AS (1)
Similarly, BP = BQ (2)
and CR = CQ (3)
and DR = DS (4)
Adding, all the four equation we get:
AP + BP + CR + DR = AS + BQ + CQ + DS
=> (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
=> AB + CD = AD + BC
Hence, proved.
问题6:在两个同心圆中,外圆的半径为5厘米,长8厘米的弦AC与内圆相切。求内圆的半径。
解决方案:
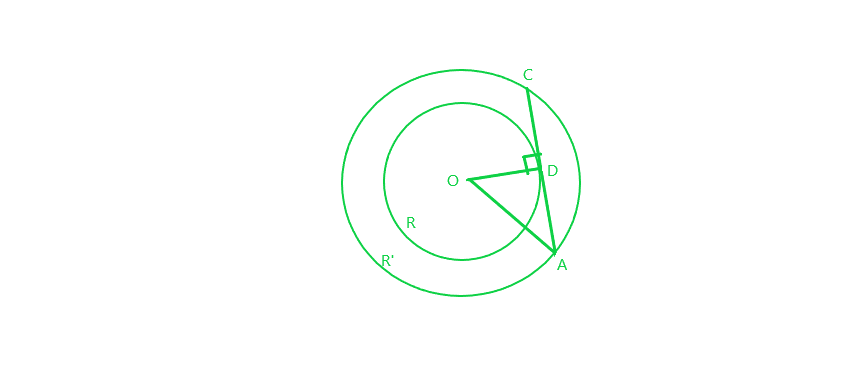
Let R and R’ be the two circles having same centre O. AC is a chord which touches the R at point D
Now, OD ⊥ AC
AD = DC = 4 cm [perpendicular line OD bisects the chord at D]
OA = 5 cm [given]
Therefore, In right-angled ∆AOD, by applying Pythagoras theorem:
OA² = AD² + OD²
=> OD² = 5² – 4² = 25 – 16 = 9
=> OD = 3 cm
Thus, Radius of the inner circle OD = 3 cm
问题 7. 圆的弦 PQ 平行于在圆的 R 点绘制的切线。证明 R平分弧 PRQ。
解决方案:
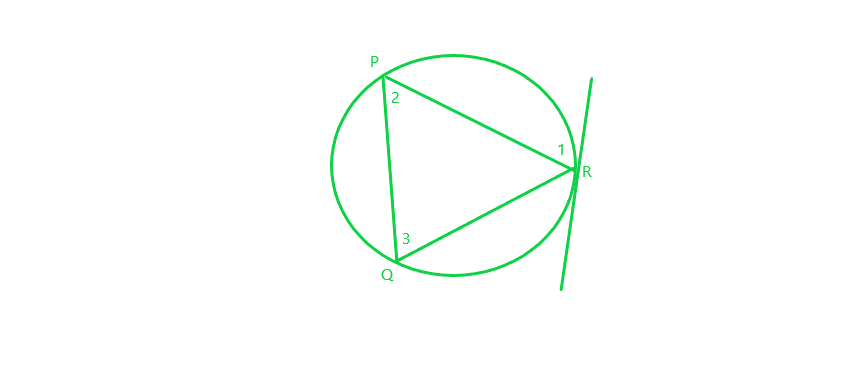
Given: Chord PQ is parallel to the tangent at R.
To prove : R bisects the arc PRQ (i.e., PR=QR)
Proof:
∠1 = ∠2 [alternate interior angles] (1)
∠1 = ∠3 [angle between tangent and chord is equal to angle made by chord in alternate segment] (2)
=> ∠2 = ∠3 [from (1) and (2)]
=> PR = QR [sides opposite to equal angles are equal]
So, R bisects PQ
问题 8. 证明一个圆的直径 AB 平分所有平行于 A 点切线的弦。
解决方案:

Given:
AB is a diameter of the circle.
A tangent is drawn from point A.
A chord CD parallel to the tangent FAG.
To prove: AB bisect CD and hence all the chords parallel to the tangent at the point A.
Proof: CD is a chord of the circle and OA is a radius of the circle.
∠FAO = 90° [Tangent at any point of a circle is perpendicular to the radius through the point of contact]
∠COB = ∠FAO [corresponding angles]
=> ∠COB = 90°
Thus, AB bisects CD [perpendicular from centre of circle to chord bisects the chord]
Similarly, the diameter AB bisects all the chords which are parallel to the tangent at the point A.
问题 9. 如果 AB、AC、PQ 是图中的切线,且 AB = 5 cm,求 ΔAPQ 的周长。
解决方案:

AB, AC and PQ are the tangents to the circle as shown in the figure above and AB = 5 cm
PB and PR are the tangents to the circle from the same point P
=> PB = PR
Similarly, QC and QR are the tangents from the same point Q
=> QC = QR
Also, AB and AC are the tangents from A
=> AB = AC = 5 cm
Now perimeter of ∆APQ
= AP + PQ + AQ
= AP + PR + RQ + AQ
= AP + PB + QC + AQ {because PB = PR and QC = QR}
= AB + AC
= 5 cm + 5 cm
=10 cm
So, Perimeter of the triangle APQ is 10 cm
问题 10.证明圆的两条平行切线之间的切线在圆心处对着直角。
解决方案:
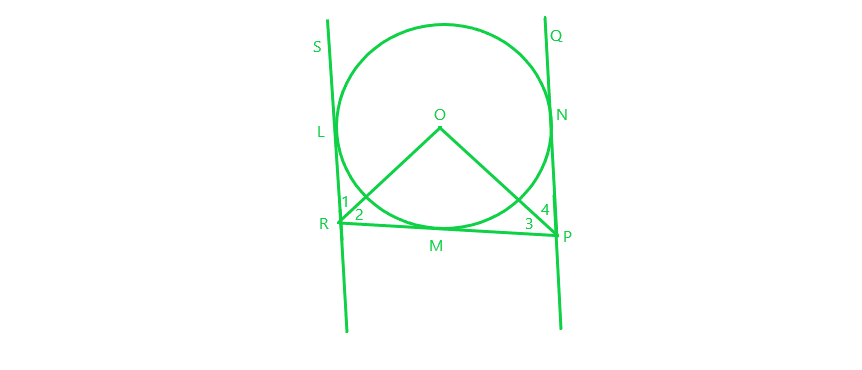
Given:
PQ and RS are parallel tangents of a circle
RMP is the intercept of the tangent between PQ and RS
RS and PQ are joined at the centre of the circle O
To prove: ∠ROP = 90°
Proof:
Since RL and RM are tangents from R and RO is joined at the centre of the circle, it will bisect the angle
=> ∠1 = ∠2 (1)
Similarly, PM and PN are tangents from P and PO is joined at the centre of the circle, it will bisect the angle
=> ∠4 = ∠3 (2)
Adding (1) and (2), we get:
∠1+∠4 = ∠2+∠3 (3)
Also, ∠LRP + ∠RPQ = 180° [co-interior angles]
=> ∠1+∠2+∠3+∠4 = 180°
=> ∠2+∠2+∠3+∠3 = 180° [using (3)]
=> ∠2+∠3 = 90° (4)
Also, in ∆POR:
∠2+∠3+∠O = 180° [sum of all the angles of triangle is 180°]
=> 90° + ∠O = 180°
=> ∠O = 90°
So, ∠ROP = 90°
Hence Proved