第 12 类 RD Sharma 解决方案 - 第 10 章可微性 - 练习 10.1
问题 1. 证明 f(x) = |x – 3|在 x = 3 处连续但不可微。
解决方案:
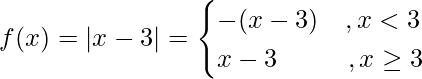
f(3) = 3 – 3 = 0
![]()
![]()
=![]()
= 0
![]()
![]()
![]()
= 0
Since LHL = RHL, f(x) is continuous at x = 3.
Now, ![]()
![]()
= –1
![]()
![]()
= 1
Since (LHD at x = 3) ≠ (RHD at x = 3)
f(x) is continuous but not differentiable at x =3.
问题 2. 证明 f (x) = x 1/3在 x = 0 处不可微。
解决方案:
(LHD at x = 0) = ![]()
![]()
![]()
= Undefined
(RHD at x = 0) = ![]()
![]()
![]()
= Undefined
Clearly LHD and RHD do not exist at 0.
f(x) is not differentiable at x = 0.
问题 3. 证明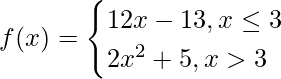 在 x = 3 处可微。
在 x = 3 处可微。
解决方案:
(LHD at x = 3) = ![]()
![]()
= 12
RHD at x = 3 = ![]()
![]()
= 12
Since LHL = RHL
f(x) is differentiable at x = 3.
问题 4. 证明如下定义的函数f 在 x = 2 处是连续的,但在 x = 2 处不可微:
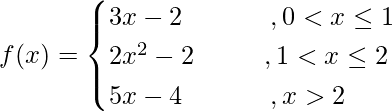
解决方案:
f(2) = 2(2)2 – 2 = 6
![]()
![]()
= 8 – 2
= 6
![]()
![]()
![]()
= 6
Clearly LHL = RHL at x = 2
Hence f(x) is differentiable at x = 2.
问题 5. 讨论函数f(x) = |x| 的连续性和可微性+ |x -1|在 (-1, 2) 的区间内。
解决方案:
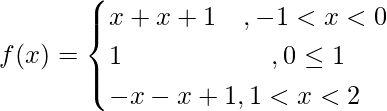
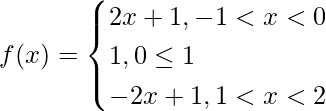
(LHD at x = 0) = ![]()
![]()
= 2
(RHD at x = 0) = ![]()
![]()
= 0
Thus, f(x) is not differentiable at x = 0.
问题 6. 找出以下函数在 x = 1 和 x = 2 处是否可微。
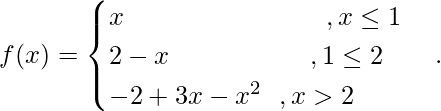
解决方案:
(LHD at x = 1) = ![]()
![]()
= 1
(RHD at x = 1) = ![]()
![]()
= –1
Clearly LHD ≠ RHD at x = 1
So f(x) is not differentiable at x = 1.
(LHD at x = 2) = ![]()
![]()
= –1
(RHD at x = 2) = ![]()
![]()
= –1
Clearly LHL = RHL at x = 2
Hence f(x) is differentiable at x = 2.
问题 7(i)。显示![由 QuickLaTeX.com 渲染 f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_10_Differentiability_%E2%80%93_Exercise_10.1_43.jpg) 如果 m>1,则在 x = 0 处可微。
如果 m>1,则在 x = 0 处可微。
解决方案:
(LHD at x = 0) = ![]()
![]()
![]()
= 0 × k
= 0
(RHD at x = 0) ![]()
![]()
![]()
= 0 × k
= 0
Clearly LHL = RHL at x = 0
Hence f(x) is differentiable at x = 0.
问题 7(ii) 证明![由 QuickLaTeX.com 渲染 f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_10_Differentiability_%E2%80%93_Exercise_10.1_50.jpg) 如果 0
如果 0
解决方案:
(LHD at x = 0) ![]()
![]()
![]()
= Not defined
(RHD at x = 0) ![]()
![]()
![]()
= Not defined
Clearly f(x) is not differentiable at x = 0.
问题 7(iii)证明![由 QuickLaTeX.com 渲染 f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_10_Differentiability_%E2%80%93_Exercise_10.1_57.jpg) 如果 m≤0 ,则在 x = 0 处不可微。
如果 m≤0 ,则在 x = 0 处不可微。
解决方案:
(LHD at x = 0) ![]()
![]()
![]()
= Not defined
(RHD at x = 0) ![]()
![]()
![]()
= Not defined
Clearly f(x) is not differentiable at x = 0.
问题 8. 求 a 和 b 的值使得函数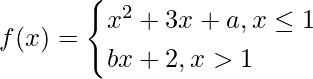 在 x 的每个实数值处可微。
在 x 的每个实数值处可微。
解决方案:
(LHD at x = 1) = ![]()
![]()
= 5
(RHD at x = 2) =![]()
![]()
= b
Since f(x) is differentiable at x = 1,so
b = 5
Hence, 4 + a = b + 2
or, a = 7 – 4 = 3
Hence, a = 3 and b = 5.
问题 9. 证明函数![由 QuickLaTeX.com 渲染 f(x) = \begin{cases}|2x-3|[x]\ \ \ \ \ \ \ \ ,x\ge 1\\sin[\frac{πx}{2}]\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x<1\end{cases}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_10_Differentiability_%E2%80%93_Exercise_10.1_69.jpg) 在 x = 1 处不可微。
在 x = 1 处不可微。
解决方案:
(LHD at x = 1) = ![]()
![]()
![]()
= 0
(RHD at x =1) = ![]()
![]()
![]()
= –2
Since (LHD at x = 1) ≠ (RHD at x = 1)
f(x) is continuous but not differentiable at x =1.
问题 10. 如果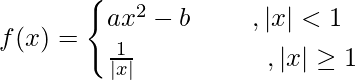 在 x = 1 处可微,求 a 和 b。
在 x = 1 处可微,求 a 和 b。
解决方案:
We know f(x) is continuous at x = 1.
So, a – b = 1 …..(1)
(LHD at x = 1) = ![]()
![]()
Using (1), we get
![]()
= 2a
(RHD at x =1) ![]()
![]()
= –1
Since f(x) is differentiable, LHL = RHL
or, 2a = –1
a = –1/2
Substituting a = –1/2 in (1), we get,
b = –1/2 – 1
b = –3/2