第 12 类 RD Sharma 解决方案 – 第 10 章可微性 – 练习 10.2

问题 1. 如果 f 由 f(x) = x ²定义，求 f'(2)。

解决方案：

$f'(2) = lim_{h\to0}\frac{f(2+h)-f(2)}{h}$

$= lim_{h\to0}\frac{(2+h)^2-2^2}{h}$

$= lim_{h\to0}\frac{4+h^2+4h-4}{h}$

$= lim_{h\to0}(4+h)$

Hence, f'(2) = 4.

问题 2. 如果 f 由 f(x) = x ² – 4x + 7 定义，证明 f'(5) = 2f'(7/2)。

解决方案：

$f'(5) = lim_{h\to0}\frac{f(5+h)-f(5)}{h}$

= $lim_{h\to0}\frac{((5+h^2)-4(5+h)+7)-(25-20+7)}{h}$

$= lim_{h\to0}\frac{h^2+25+10h-20-4h+7-12}{h}$

$= lim_{h\to0}\frac{h^2+6h}{h}$

f'(5) = 6                                      …….(1)

$f'(7/2) = lim_{h\to0}\frac{f(7/2+h)-f(7/2)}{h}$

$= lim_{h\to0}\frac{h^2+7h-14-4h+7+14-7}{h}$

$= lim_{h\to0}\frac{h^2+3h}{h}$

$= lim_{h\to0}(h+3)$

f'(7/2) = 3

⇒ 2f'(7/2) = 6                           ……(2)

From (1) and (2)

 f'(5) = 2f'(7/2).

问题 3. 证明由 f(x) = 2x ³ – 9x ² +12x + 9 在 x = 1 和 x = 2 处给出的函数f 的导数相等。

解决方案：

$f'(1) = lim_{h\to0}\frac{f(1+h)-f(1)}{h}$

$= lim_{h\to0}\frac{[2(1+h)^2-9(1+h)^2+12(1+h)+9]-[2-9+12-9]}{h}$

$= lim_{h\to0}\frac{2+2h^3+6h^2+6h-9-9h^2-18h+12+12h+9-14}{h}$

$= lim_{h\to0}\frac{2h^3-3h^2}{h}$

$= lim_{h\to0}h(2h-3)$

⇒ f'(1) = 0

Now, $f'(2) = lim_{h\to0}\frac{f(2+h)-f(2)}{h}$

$= lim_{h\to0}\frac{[2(2+h)^3-9(2+h)^2+12(2+h)+9]-[16-36+24+9]}{h}$

$= lim_{h\to0}\frac{2h^3-3h^2}{h}$

$= lim_{h\to0}h(2h-3)$

⇒ f'(2) = 0

Hence f'(1) = f'(2) = 0.

问题 4. 如果函数f(x) = ax ² + 7x – 4, f'(5) = 97，求 a。

解决方案：

$f'(5) = lim_{h\to0}\frac{f(5+h)-f(5)}{h}$

$⇒ 97 = lim_{h\to0}\frac{a(25+h^2+10h)+35+7h-4-25a-35+4}{h}$

$= lim_{h\to0}\frac{25a+ah^2+10ah-25a+7h}{h}$

$= lim_{h\to0}\frac{ah^2+h(10a+7)}{h}$

⇒ 97 = 10a +7

⇒ 10a = 90

⇒ a = 9

问题 5. 如果 f(x) = x ³ + 7x ² + 8x – 9，求 f'(4)。

解决方案：

$f'(4) = lim_{h\to0}\frac{f(4+h)-f(4)}{h}$

$= lim_{h\to0}\frac{[(4+h)^3+7(4+h)^2+8(4+h)-9]-[64+112+32-9]}{h}$

$= lim_{h\to0}\frac{64+h^3+48h+12h^2+112+7h^2+56h+32+8h-9]-[210-9]}{h}$

$= lim_{h\to0}\frac{h^3+19h^2+112h}{h}$

$= lim_{h\to0}\frac{h(h^2+19h+112)}{h}$

⇒ f'(4) = 112

问题 6. 求 f(x) = mx + c 在 x = 0 处的导数。

解决方案：

$f'(0) = lim_{h\to0}\frac{f(0+h)-f(0)}{h}$

$= lim_{h\to0}\frac{f(h)-h(0)}{h}$

$= lim_{h\to0}\frac{(mh+c)-(c)}{h}$

$= lim_{h\to0}\frac{mh+c-c}{h}$

$= lim_{h\to0}\frac{mh}{h}$

⇒ f'(0) = m.

问题 7. 检查可微性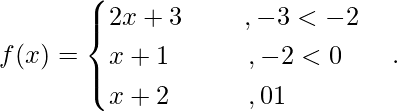$f(x) = \begin{cases}2x+3\ \ \ \ \ \ \ ,-3\lex<-2\\x+1\ \ \ \ \ \ \ \ \ ,-2\lex<0\\x+2\ \ \ \ \ \ \ \ \ ,0\lex1\end{cases}.$

解决方案：

Since f(x) is a polynomial function, it is continuous and differentiable everywhere.

Differentiability at x = –2

$(LHD at x = -2) = lim_{h\to-2^-}\frac{f(x)-f(-2)}{x-(-2)}$

$= lim_{h\to-2^-}\frac{2x+3+1}{x+2}$

$= lim_{h\to-2^-}\frac{2(x+2)}{x+2}$

= 2

$(RHD at x = -2) = lim_{h\to-2^+}\frac{f(x)-f(-2)}{x-(-2)}$

$= lim_{h\to-2^-}\frac{x+1+1}{x+2}$

$= lim_{h\to-2^-}\frac{x+2}{x+2}$

= 1

Since, LHD at x = –2  ≠ RHD at x = –2

Hence f(x) is not differentiable at x = –2.

Now, Differentiability at x = 0

(LHD at x = 0) $= lim_{h\to0}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{x+1-2}{x}$

$= lim_{h\to0}\frac{x-1}{x}$

= ∞

(RHD at x = 0) $= lim_{h\to0}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{x+2-2}{x}$

$= lim_{h\to0}\frac{x}{x}$

= 1

Since, LHD at x = –2  ≠ RHD at x = 0

Hence f(x) is not differentiable at x = 0.

问题 8. 写一个函数的例子，它处处连续但不能在恰好五个点上微分。

解决方案：

We know the modulus function f(x) = |x| is continuous but not differentiable at x = 0.

Hence, f(x) = |x| + |x – 1| + |x – 2| + |x – 3| + |x – 4| is continuous but not fails to be differentiable at x = 0,1,2,3,4.

问题 9. 讨论 f(x) = |log|x|| 的连续性和可微性。

解决方案：

Graph of f(x) = |log|x||:

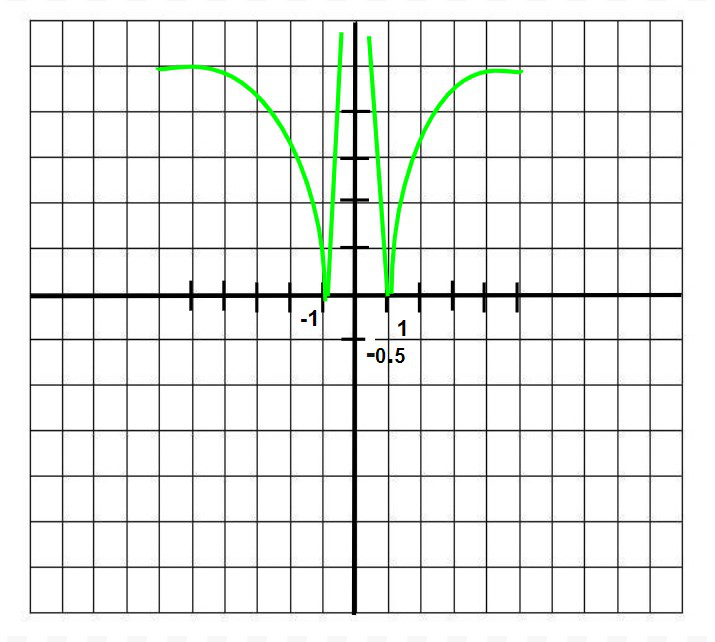
From the graph above, it is clear that f(x) is continuous everywhere, but not differentiable at 1 and -1.

问题 10.讨论 f(x) = e ^|x|的连续性和可微性.

解决方案：

$f(x) = e|x| = \begin{cases}e^{-x} \ \ \ \ \ \ \ \ ,x<0\\e^x\ \ \ \ \ \ \ \ \ \ ,x\ge 0\end{cases}$

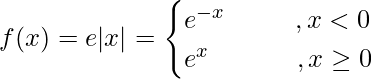
For continuity:

(LHL at x = 0) $= lim_{x\to0^-}f(x)$

= $lim_{h\to0}f(0-h)$

$= lim_{h\to0}e^{0-h}$

$= lim_{h\to0}e^{-h}$

= e⁰

= 1

(RHL at x = 0) $= lim_{x\to0^+}f(x)$

$= lim_{h\to0}f(0+h)$

$= lim_{h\to0}e^{0+h}$

$= lim_{h\to0}e^h$

= e⁰

= 1

Hence f(x) is continuous at x = 0.

For Differentiability:

(LHD at x = 0) = $lim_{x\to0^-}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{e^h-1}{-h}$

= –1

(RHD at x = 0) $= lim_{x\to0^+}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{e^h-1}{h}$

= 1

Thus, f(x) is not differentiable at x = 0.

问题 11. 讨论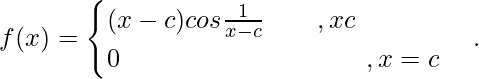$f(x) = \begin{cases}(x-c)cos\frac{1}{x-c}\ \ \ \ \ \ ,x≠c\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=c\end{cases}.$

解决方案：

(LHD at x = c) $= lim_{x\to c^-}\frac{f(c-h)-f(c)}{-h}$

$= lim_{h\to0}\frac{cos(-1/h)}{h}$

$= lim_{h\to0}\frac{cos(1/h)}{h}$

= k

(RHD at x = c) = $lim_{x\to c^+}\frac{f(c+h)-f(c)}{h}$

$= lim_{h\to0}\frac{cos(1/h)}{h}$

= k

Clearly (LHD at x = c) = (RHD at x = c) 

f(x) is differentiable at x = c.

问题 12. 是 |sinx|可微分？ cos|x|呢？

解决方案：

$f(x) = |sinx| = \begin{cases}-sinx \ \ \ \ \ \ \ \ , x<nπ\\sinx \ \ \ \ \ \ \ \ \ \ \ ,x>nπ\end{cases}$

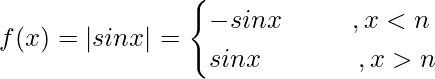
 (LHD at x = nπ) $= lim_{x\to nπ^-}\frac{f(x)-f(nπ)}{x-nπ}$

$= lim_{h\to0}\frac{-sin(nπ-h)-sinnπ}{nπ-h-nπ}$

$= lim_{h\to0}\frac{sinh}{-h}$

= –1

 (RHD at x = nπ) $= lim_{h\to0}\frac{sin(nπ+h)-sinnπ}{h}$

$= lim_{h\to0}\frac{sinh}{-h}$

= 1

Since, LHD at x = nπ  ≠ RHD at x = nπ

Hence f(x) = |sinx|  is not differentiable at x = nπ.

Now, f(x) = cos|x|

Since, cos(–x) = cosx

Thus, f(x) = cos x

Hence f(x) = cos|x| is differentiable everywhere.