10类NCERT解决方案-第7章坐标几何-练习7.4

问题1.确定比率，其中线2x + y – 4 = 0划分连接点A(2，-2)和B(3，7)的线段。

Given: 2x + y – 4 = 0 line divides the line segment joining the points A(2, -2) and B(3, 7)

Find: Ratio in which the given line divides the line segment joining the points A and B

So, the co-ordinates of C is $[\frac{m_1x_2+m_2x_1}{m1+m2},\frac{m_1y_2+m_2y_1}{m1+m2}]$

Now, let us considered the ratio is k:1

= $[\frac{k(3)+1(2)}{k+1},\frac{k(7)+(-2)}{k+1}]$

= $(\frac{3k+2}{k+1}\frac{7k}{k+1})$

But c lies on 2x+y-4=0

So, 

2$[\frac{3k+2}{k+1}+[\frac{7k}{k+1}]$ – 4 = 0

$\frac{6k+4}{k+1}+\frac{7k-2}{k+1}-\frac{4}{2}=0$

$\frac{6k+4+7k-2-4(k+1)}{k+1}=\frac{0}{1}$

$\frac{6k+4+7k-2-4k-4}{13k-4k-2}=\frac{0}{0}$

9k = 2

k/1 = 2/9

Hence, the ratio is 2:9

问题2.如果点(x，y)，(1、2)和(7，0)是共线的，则找到x与y之间的关系。

Find: Here, we have to find a relation between x and y, if the points (x, y), (1, 2), and (7, 0) are collinear.

If the given points are collinear then the area of the triangle is 0(created using these points).

So, 

Area of triangle = 1/2[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0

=> x(2 – 0) + 1(0 – y) + 7(y – 2) = 0

=> x(2)+ 1(-y) + 7y – 14 = 0

=> 2x – y + 7y – 14 = 0

=> 2x + 6y – 14 = 0

On dividing by 2 on both sides, we get  

x + 3y – 7 = 0

Hence, the required relation is x + 3y – 7 = 0 

问题3.找到通过点(6，-6)，(3，-7)和(3，3)的圆心。

Let us considered point A(6, -6), B(3, -7), and C(3, 3) and P(x, y) is the center of the circle.

So, AP = BP = CP(radii are equal)

Now first we take

AP = BP

√((x₂ – x₁)² + (y₂ – y₁)²) = √((x₂ – x₁)² + (y₂ – y₁)²)

(x – 6)² + (y + 6)² = (x – 3)² + (y + 7)²

x² + 36 – 12x + y² + 36 + 12y = x² + 9 – 6x + y² + 49 + 14y

36 – 12x + 36 + 12y = 9 – 6x + 49 + 14y

-12x + bx + 12y – 14y + 72 – 58 = 0

-6x – 2y + 14 = 0

6x + 2y – 14 = 0

On divided by 2 on both side, we get

3x + y – 7 = 0          -(1) 

Now, we take 

BP = CP

√((x₂ – x₁)² + (y₂ – y₁)²) = √((x₂ – x₁)² + (y₂ – y₁)²)

(x – 3)² + (y + 7)² = (x – 3)² + (y – 3)²

y² + 7² + 2(y)(7) = y² + 3² – 2(y)(3)

49 + 14y = 9 – 6y

14y + 6y = 9 – 49

20y = -40

y = -40/20

y = -2

Now, on putting value of y = -2 in eq(1), we get

3x – 2 – 7 = 0

3x – 9 = 0

3x = 9

X = 9/3 = 3

Hence, the center P(x, y) = (3, -2)  

问题4.正方形的两个相对顶点是(-1，2)和(3，2)。查找其他两个顶点的坐标。

Let us considered ABDC is a square, and its two opposite vertices are A(-1, 2) and C(3, 2). 

Let point O intersect line AC and BD. 

Now, first we will find the coordinate of point O(x, y)

As we know that O is the mid point of line AC,

x = (3 – 1)/2 = 1 

y = (2 + 2)/2 = 2 

So, the coordinate of point O is (1, 2)

Now we will find the side of the Square

AC = √((3 + 1)² + (2 – 2)²) 

AC = √16 = 4

So in triangle ACD, using hypotenuse theorem, we get

a = 2√2

So, each side of the square is 2√2

For the coordinate of D: 

Let us assume that the coordinate of D is (x₁, y₁).

As we know that the sides of the squares are equal

so, AD = CD

√((x₂ – x₁)² + (y₂ – y₁)²) = √((x₂ – x₁)² + (y₂ – y₁)²)

√(x₁ + 1)² + (y₁ – 2)² = √(x₁ – 3)² + (y₁ – 2)²

(x₁ + 1)² + (y₁ – 2)² = (x₁ – 3)² + (y₁ – 2)²

(x₁ + 1)² = (x₁ – 3)²

x₁² + 1 + 2x₁ = x₁² + 9 – 6x₁

1 + 2x₁ = 9 – 6x₁

2x₁ + 6x₁ = 9 – 1

8x₁ = 8

x₁ = 1

Now, CD² = ((x₂ – x₁)² + (y₂ – y₁)²)

8 = (x₁ – 3)² + (y₁ – 2)²

8 = x₁² + 9 – 6x₁ + y₁² + 4 – 4y₁

y₁ – 2 =2

y₁ = 4

So the coordinate of D is (1, 4)

For the coordinate of B:

Let B(x₂, y₂) and as we know BOD is a line segment so, 

1 = x₂ + 1/2 

x₂ = 1

2 = y₂ + 4/2 

y₂ = 0

So the coordinate of B = (1, 0)

问题5.克里希纳格尔的X年级学生学校已为他们的园艺活动分配了一块长方形的土地。古尔莫哈尔(Gulmohar)的树苗被种植在边界上，彼此之间的距离为1 m。如图所示，图中有三角形的草皮草坪。学生将在该地块的其余区域播种开花植物的种子。

(i)以A为原点，找到三角形顶点的坐标。

(ii)如果C是原点，则∆PQR的顶点坐标将是什么?

此外，在这种情况下，请计算三角形的面积。你观察到什么?

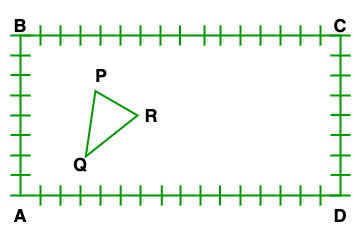
(i) Now taking A as an origin the coordinates of the vertices of the triangle are 

P = (4, 6)

Q = (3, 2)

R = (6, 5)

(ii) Now taking C as an origin the coordinates of the vertices of the triangle are

P = (12, 2)

Q = (13, 6)

R = (10, 3) 

Finding the area of triangle, when A as a origin the coordinates of the vertices

of the triangle are P(4, 6), Q(3, 2), and R(6, 5)

Area1 = 1/2[x₁(y₂ – y₃) + x2(y₃ – y₁) + x₃(y₁ – y₂)]

= [4(2 – 5) + 3(5 – 6) + 6(6 – 2)]/2

= [-12 – 3 + 24]/2

= [-15 + 24]/2

= 9/2 sq. unit

Finding the area of triangle, when C as a origin the coordinates of the vertices

 of the triangle are P(12, 2), Q(13, 6), and R(10, 3)

Area2 = [12(6 – 3) + 13(3 – 2) + 10(2 – 6)]/2

= [12(3) + 13(1) + 10(-4)]/2

= [36 + 13 – 40]/2

= [49 – 40]/2

= 9/2 Sq.unit

So, here we observed that the Area1 = Area2

问题6.ΔABC的顶点是A(4，6)，B(1、5)和C(7，2)。绘制一条线以分别在D和E处与AB和AC边相交，使得AD / AB = AE / AC = 1/4。计算ΔADE的面积，并将其与ΔABC的面积进行比较。

解决方案：

Given: AD/AB = AE/AC = 1/4

To find: Area of ∆ADE

Since D and E divides AB and AC is the same ratio 1:4 then DE||BC           -(Using theorem 6.2)

Now, In ∆ADE and ∆ABC

∠A = ∠A         -(Common angle)

∠D = ∠B         -(Corresponding  angles)

∴∆ADE~∆ABC          -(AA similarity)

ar.(ADE)/ar.(ABC) = (AD/AB)² = 1/16          

Area of ∆ABC = 1/2[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

= [4(5 – 2) + 1(2 – 6) + 7(6 – 5)]/2

= [4(3) + 1(-4) + 7(1)]/2

= [12 – 4 + 7]/2

= [19 – 4]/2         

= 15/2 sq.unit

ar.(ADE)/ar.(ABC) = -(1/10)

ar.(ADE) = (1/16) × ar.(ABC)

ar.(ADE) = (1/16) × (15/2) = 15/32 sq.unit

So, we get

ar.(ADE):ar.(ABC) = 1:16

问题7让A(4，2)，B(6，5)和C(1，4)成为ΔABC的顶点。

(i)BC在D处的A米的中位数。找到D点的坐标。

(ii)在AD上找到点P的坐标，以使AP：PD = 2：1。

(iii)分别在中位数BE和CF上找到点Q和R的坐标，以使BQ：QE = 2：1和CR：RF = 2：1。

(iv)您观察到什么?

[注意：这三个中位数共有的点称为质心，该点将每个中位数按比例2：1划分]

(v)如果A(x1，y1)，B(x2，y2)和C(x3，y3)是∆ABC的顶点，请找到三角形质心的坐标。

解决方案：

Given: The vertices of ∆ABC are A(4, 2), B(6, 5) and C(1, 4)

(i) Co-ordinates of D = Midpoint of BC

= $[\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]$

= $[\frac{6+1}{2},\frac{5+4}{2}]$

= [7/2, 9/2]

= (3.5, 4.5)

(ii) Co-ordinates of P =$[\frac{m_1x_1+m_2x_2}{2},\frac{m_1y_1+m_2y_2}{2}]$

= $[\frac{(3.5)2+1(4)}{2+1},\frac{(4.5)2+1(2)}{2+1}]$

= $[\frac{7+4}{3},\frac{9+2}{3}]$

= [11/3, 11/3]

(iii) Co-ordinates E = Midpoint of AC 

= $[\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]$

= $[\frac{4+1}{2},\frac{2+4}{2}]$

= (2.5, 3)

(iv) We observe that the points P, Q and R coincide, i.e the medians of AD, BE, and 

concurrent at the point [11/3, 11/3]. This point is known as the centroid of the triangle.

(v) As AD is median, thus D is midpoint of BC

So the co-ordinates of D:

= $[\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]$

= $[\frac{x_2+x_3}{2},\frac{y_2+y_3}{2}]$

Co-ordinates of G:

= [\frac{x_2m_1+m_2x_1 }{m_1+m_2},\frac{y_2m_1+y_1m_12}{m_1+m_2}]                                   

问题8. ABCD是由点A(-1，-1)，B(-1、4)，C(5、4)和D(5，-1)，P，Q，R和S组成的矩形分别是AB，BC，CD和DA的中点。四边形PQRS是正方形吗?一个矩形?还是菱形?证明你的答案。

解决方案：

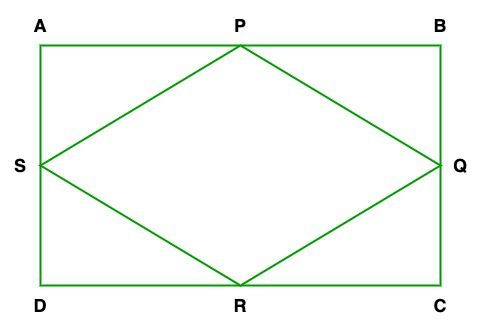
Given: Points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1) and P, Q, R and S are the mid-points of AB, BC, CD, and DA 

So, 

$P(\frac{-1-1}{2},\frac{-1+1}{2})$ = (-2/2, -1, 3/2)

$Q(\frac{-1+5}{2},\frac{4+4}{3})$ = (4/2, 8/2) = (2, 4)

$R(\frac{5+5}{2},\frac{4-1}{2})$ = (10/2, 8/2) = (5, 3/2)

$S(\frac{5-1}{2},\frac{-1-1}{2})$ = (4/2, -2/2) = (2, 1)

So, the length of $PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

$=\sqrt{(2+1)^2+(4-\frac{3}{2})^2}$

$=\sqrt{(3)^2+(\frac{5}{2})^2}$

$=\sqrt{9+\frac{25}{2}}$

= √(61/4)

The length of $QR=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

$=\sqrt{(3)^2+(\frac{-5}{2})^2}$  

$=\sqrt{9+\frac{25}{4}}$

= √(61/4)

The length of $RS=\sqrt{(2-5)^2+(21-\frac{3}{2})^2}$

$=\sqrt{(-3)^2+(\frac{-5}{2})^2}$

$=\sqrt{9+\frac{25}{4}}$

= √(61/4)

The length of $SP=\sqrt{(-1-2)^2+(\frac{3}{2}+1)^2}$

$=\sqrt{(-3)^2+(\frac{5}{2})^2}$

$=\sqrt{9+\frac{25}{4}}$

= √(61/4)

The length of the diagonal $QS=\sqrt{(2-2)^2+(-1-4)^2}$

 $=\sqrt{(0)^2+(-5)^2}$

= √25 = 5 

The length of the diagonal $PR=\sqrt{(5+1)^2+(\frac{3}{2}\frac{-3}{2})^2}$

$=\sqrt{(6)^2+(0)^2}$  

= √36 = 6                 

Hence, all fours sides are equal(i.e., PQ = QR = RS = SP) but the diagonals are 

not equal to each other(i.e. QS ≠ PR). 

Therefore, given quadrilateral PQRS is a rhombus.