第11类RD Sharma解决方案–第24章圈子–练习24.2

问题1(i)。找到圆心x ² + y ² + 6x – 8y – 24 = 0的中心坐标。

解决方案：

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Centre = (-g, -f)

Radius = $\sqrt{g^2+f^2-c}$

Given equation of circle is x² + y² + 6x – 8y – 24 = 0

On comparing with eq(i), we get

Hence, g = 3, f = -4, c = -24

So, 

Centre = (-3, 4)

Radius = 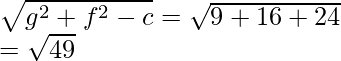$\sqrt{g^2+f^2-c}=\sqrt{9+16+24}\\ =\sqrt{49}$

Radius = 7

问题1(ii)。找到圆的中心和半径的坐标2x ² + 2y ² – 3x + 5y = 7。

解决方案：

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Centre = (-g, -f)

Radius = $\sqrt{g^2+f^2-c}$

Given equation of circle is 2x² + 2y² – 3x + 5y – 7 = 0

x² + y² – 3/2x + 5/2y – 7/2 = 0

On comparing with eq(i), we get

Hence, g = -3/4, f = 5/4, c = -7/2

So, center = (3/4, -5/4)

Radius = 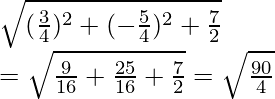$\sqrt{(\frac{3}{4})^2+(-\frac{5}{4})^2+\frac{7}{2}}\\ =\sqrt{\frac{9}{16}+\frac{25}{16}+\frac{7}{2}}=\sqrt{\frac{90}{4}}$

Radius = 3√10/4 

问题1(iii)。找到圆的中心和半径的坐标1/2(x ² + y ² )+ xcosθ+ ysinθ– 4 = 0。

解决方案：

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Centre = (-g, -f)

Radius = $\sqrt{g^2+f^2-c}$

Given equation of circle is 1/2(x² + y²) + x cosθ + y sinθ – 4 = 0

⇒ x² + y² + 2x cosθ + 2sin θ – 8 = 0

On comparing with eq(i), we get

Hence, g = cos θ, f = sin θ, c = -8

So, centre = (-cos θ, -sinθ)

Radius = $\sqrt{\cos^2θ+\sin^2θ+8}=\sqrt{1+8}=3$

Radius = 3

问题1(iv)。找到圆的中心和半径的坐标x ² + y ² –轴– by = 0。

解决方案：

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Centre = (-g, -f)

Radius = $\sqrt{g^2+f^2-c}$

Given equation of circle is x² + y² – ax – by = 0

On comparing with eq(i), we get

Hence, g = -a/2, f = -b/2, c = 0  

So, centre = (a/2, b/2) 

Radius = $\sqrt{\frac{a^2}{4}+\frac{b^2}{4}+0}=\frac{\sqrt{a^2+b^2}}{2}$

Radius = $\frac{a^2+b^2}{2}$

问题2(i)。找到通过点(5，7)，(8，1)和(1，3)的圆的方程。

解决方案：

Given that, the circle pass through points P(5, 7), Q(8, 1), and R(1, 3)

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Since, P, Q, and R lies on eq(i)

So, 

25 + 49 + 10g + 14f + c = 0 …….(ii)

64 + 1 + 16g + 2f + c = 0  …….(iii)

1 + 9 + 2g + 6f + c = 0  ……(iv)

Now on solving eq (ii), (iii), and (iv), we get,

g = -29/6, f = -19/6, c = 56/3

Now put all these values in eq(i), we get

The equation of circle is  

x² + y² – 29/3x – 19/6y + 56/3 = 0 

3(x² + y²) – 29x – 19y + 56 = 0

问题2(ii)。找到通过点(1、2)，(3，-4)和(5，-6)的圆的方程。

解决方案：

Given that, the circle pass through points P(1, 2), Q(3, -4), and R(5, -6)

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Since, P, Q, and R lies on eq(i)

So, 

1 + 4 + 2g + 4f + c = 0          …..(ii)

9 + 16 + 6g – 8f + c = 0        …..(iii)

25 + 36 + 10g – 12f + c = 0      …..(iv)

Now on solving eq (ii), (iii), and (iv), we get,

g = -11, f = -2, and c = 25

Now put all these values in eq(i), we get

The equation of circle is  

x² + y² – 22x – 4y + 25 = 0

问题2(iii)。找到通过点(5，-8)，(-2、9)和(2、1)的圆的方程。

解决方案：

Given that, the circle pass through points P(5, -8), Q(-2, 9), and R(2, 1)

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Since, P, Q, and R lies on eq(i)

So, 

25 + 64 + 10g – 16f + c = 0     …..(ii)

4 + 81 – 4g + 18f + c = 0     …..(iii)

4 + 1 + 4g + 2f + c = 0      …..(iv)

Now on solving eq (ii), (iii), and (iv), we get,

g = 58, f = 24, and c = -285

Now put all these values in eq(i), we get

The equation of circle is  

x² + y² + 116x + 48y – 285 = 0         

问题2(iv)。找到通过点(0，0)，(-2，1)和(-3，2)的圆的方程。

Given that, the circle pass through points P(0, 0), Q(-2, 1), and R(-3, 2)

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Since, P, Q, and R lies on eq(i)

So, 

0 + 00 + 0 + c = 0    …..(ii)

4 + 1 – 4x + 2y + c = 0    …..(iii)

9 + 4 – 6x + 4y + c = 0     …..(iv)

Now on solving eq (ii), (iii), and (iv), we get,

g = -3/2, f = -11/2, and c = 0

Now put all these values in eq(i), we get

The equation of circle is

x² + y² – 3x – 11y = 0

问题3。找到通过(3，-2)，(-2，0)并以2x – y = 3为中心的圆的方程。

解决方案：

It is given that, the circle passing through P(3, -2) and Q(-2, 0) and having its centre on 2x – y = 3.

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Since the circle passes through (3, -2) and also (-2, 0) 

So, 

9 + 4 + 6g – 4f + c = 0    …..(ii)

4 + 0 – 4g + 0 + c = 0    …..(iii)

Also, the centre of the circle lies on 2x – y = 3

-2g + f = 3   …..(iv)

Now on solving eq (ii), (iii), and (iv), we get,

g = 3/2, f = 6, and c = 2

Now put all these values in eq(i), we get

The equation of circle is

x² + y² + 3x + 12y + 2 = 0

问题4.找到通过点(3，7)，(5，5)并以x – 4y = 1线为中心的圆的方程。

解决方案：

It is given that, the circle passing through P(3, 7) and Q(5, 5) and having its centre on x – 4y = 1

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Since the circle passes through P and Q

so, 

9 + 49 + 7g + 14f + c = 0      …..(ii)

25 + 25 + 10g + 10f + c = 0     …..(iii)

Also, the centre of the circle lies on  x – 4y = 1

so, -g + 4f = 1     …..(iv)

Now on solving eq (ii), (iii), and (iv), we get,

g = 3, f = 1, and c = -90

Now put all these values in eq(i), we get

The equation of circle is  

x² + y²+ 6x + 2y – 90 = 0

问题5。证明点(3，-2)，(1，0)，(-1，-2)和(1，-4)是循环的。

解决方案：

Given that P (3, -2), Q(1, 0), R(-1, -2), and S(1,-4)

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Since the circle passes through P, Q and R

So, 

9 + 4 + 6g – 4f + c = 0      …..(ii)

1 + 0 + 2g – 0 + c = 0      …..(iii)

1 + 4 – 2g – 4f + c = 0      …..(iv)

Now on solving eq (ii), (iii), and (iv), we get,

g = -1, f = 2 and c = 1

Now put all these values in eq(i), we get

The equation of circle is  

x² + y² – 2x + 4y + 1 = 0      …..(v)

Here, we clearly see that point S(1,-4) satisfy eq(v)

Hence, points P, Q, R, and S are concyclic  

问题6：证明点(5、5)，(6、4)，(-2、4)和(7、1)都位于一个圆上，并找到其等式，中心和半径。

解决方案：

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Centre = (-g, -f)

Radius = $\sqrt{g^2+f^2-c}$

Therefore, P(5, 5), Q(6, 4), and R(-2, 4) lie on eq(i), 

So, 

25 + 25 + 10g + 10f + c = 0      …..(ii)

36 + 16 + 12g + 8f + c = 0      …..(iii)

4 + 16 + 4g + 8f + c = 0      …..(iv)

Now on solving eq (ii), (iii), and (iv), we get,

g = -2, f = -1, c = -20

Now put all these values in eq(i), we get

The equation of circle is  

x² + y² – 4x – 2y – 20 = 0     …..(v)

Here, we clearly see that point S(7, 1)

Hence, points P, Q, R, and S are concyclic  

Now, the centre = (-g, -f) = (2, 1)

Radius = $\sqrt{g^2+f^2-c}=\sqrt{4+1+20}=\sqrt{25}=5$

问题7(i)。找出与由x + y + 3 = 0，x – y + 1 = 0和x = 3形成的三角形外接的圆的方程。

解决方案：

The equations of lines are

x + y = -3      …..(i)

x – y = -1      …..(ii)

x = 3      …..(iii)

Let us considered A, B, and C are the point of intersection of lines (i), (ii), and (iii)

So, Point A(-2,-1), B(3, 4), and C(3,-6)

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(iv)

So, the circle circumscribing the ∆ABC

4 + 1 – 4g – 2f + c = 0      …..(v)

9 + 16 + 6g + Bf + c = 0      …..(vi)

9 + 36 + 6g – 12f + c = 0      …..(vii)

Now on solving eq (v), (vi), and (vii), we get,

g = -3, f = 1, c = -15

Now put all these values in eq(iv), we get

The equation of circle is  

x² + y² – 6x + 2y – 15 = 0

问题7(ii)。找到与由线2x + y – 3 = 0，x + y – 1 = 0和3x + 2y – 5 = 0形成的三角形外接的圆的方程。

解决方案：

The equations of lines are

2x + y = 3     …..(i)

x + y = 1     …..(ii)

3x + 3y = 5     …..(iii)

Let us considered A, B, and C are the point of intersection of lines (i), (ii), and (iii)

So, A = (2, -1)

B = (3, -2)

C = (1, 1)

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(iv)

So, the circle circumscribing the ∆ABC

4 + 1 + 4g – 2f + c = 0     …..(v)

9 + 4 + 6g – 4f + c = 0     …..(vi)

1 + 1 + 2g + 2f + c = 0     …..(vii)

Now on solving eq (v), (vi), and (vii), we get,

g = -13/2, f = -5/2, and c = 16

Now put all these values in eq(iv), we get

The equation of circle is  

x² + y² – 13x – 5y + 16 = 0

问题7(iii)。求出与由直线x + y = 2、3x – 4y = 6和x – y = 0形成的三角形外接的圆的方程。

解决方案：

The equations of lines are

x + y = 2      …..(i)

3x – 4y = 6      …..(ii)

x – y = 0      …..(iii)

Let us considered A, B, and C are the point of intersection of lines (i), (ii), and (iii)

So, A = (2, 0)

B = (-6, -6)

C = (1, 1)

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(iv)

So, the circle circumscribing the ∆ABC

4 + 4g + c = 0     …..(v)

36 + 36 – 12g – 12f + c = 0     …..(vi)

1 + 1 + 2g + 2f + c = 0     …..(vii)

Now on solving eq (v), (vi), and (vii), we get,

g = 2, f = 3, and c = -12

Now put all these values in eq(iv), we get

The equation of circle is  

x² + y² + 4x + 6y – 12 = 0

问题7(iv)。找出外接由线y = x + 2，3y = 4x和2y = 3x形成的三角形的圆的方程。

解决方案：

The equations of lines are

y = x + 2      …..(i)

3y = 4x      …..(ii)

2y = 3x      …..(iii)

Let us considered A, B, and C are the point of intersection of lines (i), (ii), and (iii)

So, A = (6, 8)

B = (4, 6)

C = (0, 0)

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(iv)

So, the circle circumscribing the ∆ABC

12g + 16f + c = -100      …..(v)

8g + 12f + c = -52      …..(vi)

c = 0      …..(vii)

Now on solving eq (v), (vi), and (vii), we get,

f = 11 and g = -23

Now put all these values in eq(iv), we get

The equation of circle is  

x² + y² – 46x + 22y = 0.

问题8.证明三个圆的中心x ² + y ² – 4x – 6y – 12 = 0，x ² + y ² + 2x + 4y – 10 = 0，x ² + y ² -10x – 16y – 1 = 0是共线的。

解决方案：

The given equation of circles are,

x² + y² – 4x – 6y – 12 = 0  …….(i)

x² + y² + 2x + 4y – 10 = 0  …….(ii)

x² + y² – 10x – 16y – 1 = 0  …….(iii)

Let O1, O2 and O3 are the centres of (i), (ii), and (iii)

O1 = (-g, -f) = (2, 3)

O2 = (-g, -f) = (-1, -2)

O3 = (-g, -f) = (5, 8)

 O1, O2 and O3 will be collinear if ar(∆ O1O2O3) = 0

$ar(∆ O1O2O3)=\frac{1}{2} \begin{vmatrix} x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1 \end{vmatrix}$

$=\frac{1}{2} \begin{vmatrix} 2 & 3 & 1\\ -1 & -2 & 1 \\ 5 & 8 & 1 \end{vmatrix}=\frac{1}{2} \begin{vmatrix} 2 & 3 & 1\\ -3 & -5 & 0 \\ 3 & 5 & 0 \end{vmatrix}$

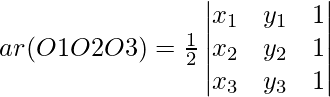
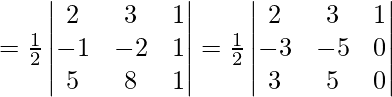
R2 ⇒ R2 ⇒ -R1

R3 ⇒ R3 ⇒ -R1

$=\frac{1}{2} \begin{vmatrix} 2 & 3 & 1\\ -1 & -2 & 1 \\ 5 & 8 & 1 \end{vmatrix}=\frac{1}{2} \begin{vmatrix} 2 & 3 & 1\\ -3 & -5 & 0 \\ 3 & 5 & 0 \end{vmatrix}$

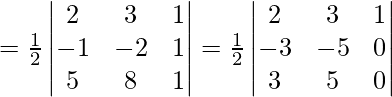
O1, O2, and O3 are collinear

问题9.证明圆的半径x ² + y ² = 1，x ² + y ² – 2x – 6y – 6 = 0，x ² + y ² – 4x – 12y – 9 = 0

解决方案：

The given equation of circles are,

x² + y² = 1 ———–(i)

x² + y² – 2x – 6y – 6 = 0 ———-(ii)

x² + y² – 4x – 12y – 9 = 0 ———-(iii)

Let us considered R1, R2, and R3 are the radii of (i), (ii), and (iii)

So, R1 = 1

R2 = $\sqrt{g^2+f^2-c}=\sqrt{1^2+3^2+6}=\sqrt{16}=4$

R3 = $\sqrt{g^2+f^2-c}=\sqrt{2^2+6^2+9}=\sqrt{49}=7$         

As we know that if a, b, c are in AP, then b = a + b/2   

so, a = 1, b = 4, c = 7, b = 1 + 7/2 = 4 

Therefore 1, 4, 7 are in AP. 

Hence, the radius of the three circles lie in AP.

问题10。找到圆的方程，该方程穿过原点并在x轴和y轴的正侧分别切掉长度为4和6的弦。

解决方案：

It is given that a circle that passes through origin O(0, 0) and 

cut off on intercepts of length 4 on x-axis and 6 on y-axis.

So, OA = 4

OB = 6

Let us assume C be the centre of the circle and 

CM and CN are perpendicular line drawn on OA and OB 

so, the coordinate of A = (4, 0) and B = (0, 6)

The coordinates of M = (2, 0) and N = (0, 3)

And the coordinates of C = (2, 3)

Now in ∆OCM, 

Using Pythagoras theorem

OC² = OM² + CM²

= 22 + 32                    

= 4 + 9

OC = √13

Hence, the required circle is

(x – 2)² + (y – 3)² = 13

x² + y² – 4x – 6y = 0

问题11。找到与圆同心圆x ² + y ² – 6x + 12y + 15 = 0并为其面积加倍的圆的方程。

解决方案：

The given equation of circle is

x² + y² – 6x + 12y + 15 = 0 …….(i)

so, centre = (-g, -f) = (3, 6)

radius  = $\sqrt{g^1+f^2-c}=\sqrt{9+36-15}=\sqrt{30}$

Now, the required equation of circle in concentric with (i) 

that means both have same centre (3,-6)

The area of required circle = 2 * Area of (i)

πR² = 2 * π(√30)²

R² = 60

R = 2√15

Hence, the required circle is

(x – 3)² + (y + 6)² = 60

x² + y² – 6x + 12y – 15 = 0

问题12。求出通过点(1，1)，(2，2)且半径为1的圆的方程。表明有两个这样的圆。

解决方案：

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

It is given that the points P(1, 1) and Q(2, 2) passes throught eq(1)

So, 

1 + 1 + 2g + 2f + c = 0     …..(ii)

4 + 4 + 4g + 4f + c = 0     …..(iii)

Its is gievn that the radius = 1

⇒$\sqrt{g^2+f^2-c}=1$

⇒ g² + f2 – c = 1   ……(iv)

Now from eq(ii) and (iii), we get

g + f + c/2 = -1  

g + f + c/4 = -2

Now on subtracting both the equations, we get

c = 4

g + f = -3  …….(v)

Now on solving eq(v) and (vi), we get

g = -1 or -2 and f = -2 or -1

Hence, the required circle is

x² + y² – 2x – 4y + 4 = 0

or 

x² + y² – 4x – 2y + 4 = 0

问题13。找到与x ² + y ² – 4x – 6x – 6y – 3 = 0同心且与y轴接触的圆的方程。

解决方案：

The given equation of circle is  

x² + y² – 4x – 6y – 3 = 0   …..(i)

so, centre = (-g, -f) = (2, 3)

The required circle is concentric with eq(i) 

so, both have centre(2, 3)

 Also, the required circle touches y-axis at A.

So, CA = radius = 2

Hence, the required circle is

(x – 2)² + (y – 3)² = 4

x² + y² – 4x – 6y + 9 = 0

问题14.如果圆通过点(0，0)，(a，0)，(0，b)，则找到其中心的坐标。

解决方案：

From the given figure, CA, CO, and AB  are the equal radii of the circle 

So, 

CA = CO = CB = r

Also, OCA is an isosceles triangle, and CM is the perpendicular bisector to the OA.

Hence  OM = a/2

Similarly, CN is the perpendicular bisector to the OB

So, ON = b/2

from the above figure, it is clear that

OM = x = a/2

ON = y = b/2

Hence the centre of the circle is c(a/2, b/2)  

问题15。找到通过点(2，3)和(4，5)的圆的方程，其中心位于直线y – 4x + 3 = 0上。

解决方案：

Its is given that a circle which passes through the point P(2, 3) and Q(4, 5) and 

the centre lies on the straight line y – 4x + 3 = 0.

As we know that the general equation of circles is

x² + y² + 2gx + 2fy + c = 0      …..(i)

Since the circle passes through P, and Q

So, 

13 + 14g + 6f + c = 0    …..(ii)

41 + 8g + 10f + c = 0    …..(iii)

Centre (-g, -f) lies on y – 4x + 3 = 0

So, -f + 4g = -3    …..(iv)

Now on subtracting eq(ii) from (iii), we get

28 + 4g + 4f = 0    …..(v)

On solving eq(iv) and (v) we get,

f = -5  and g = -2

Now put all these values in eq(i), we get

The equation of circle is  

41 – 16 – 50 + c = 0

c = 25

Hence,  the required  equation of the circle is,

x² + y² – 4x – 10y + 25 = 0