第6章衍生物的应用–第6章的其他练习|套装1
问题12.三角形的斜边上的一点与三角形的边相距a和b。证明斜边的最小长度为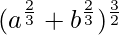
解决方案:
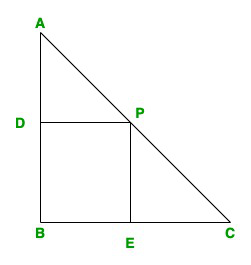
Given, a triangle ABC
Let, PE = a & PD = b
In the △ABC, ∠B = 90
Let ∠C = θ, so, ∠ DPA = θ
DP|| BC.
Now in △ADDP,
cosθ = DP/AP = b/AP
AP = b/cosθ
In △EPC,
sinθ = EP/CP = a/CP
CP = a/sin θ
Now AC = h = PA + PC
h = ![]()
h(θ) = b sec θ + a cosec θ
Put h'(θ) = ![]()
![]()
b sin3θ = a cos 3θ
tan3θ = a/b
tanθ = (a/b)1/3
secθ = ![]()
cosecθ = ![]()
hmax = ![]()
hmax = (b2/3+a2/3)3/2
问题13。找出由f(x)=(x – 2) 4 (x + 1) 3给出的函数f具有的点
(i)局部最大值
(ii)局部最小值
(iii)拐点
解决方案:
f(x) = (x – 2)4(x + 1)3
On differentiating w.r.t x, we get
f'(x) = 4(x – 2)3(x + 1)3 + 3(x + 1)2(x – 2)4
Put f'(x) = 0
(x – 2)3(x + 1)2 [4(x + 1) + 3(x – 2)] = 0
(x – 2)3(x + 1)2(7x – 2) = 0
Now,
Around x = -1, sign does not change, i.e
x = -1 is a point of inflation
Around x = 2/7, sign changes from +ve to -ve i.e.,
x = 2/7 is a point of local maxima.
Around x = 2, sign changes from -ve to +ve i.e.,
x = 2 is a point of local minima
问题14。找出由f(x)= cos 2 x + sin x,x∈[0,π]给出的函数f的绝对最大值和最小值
解决方案:
f(x) = cos2x + sin x; x ϵ [0, π]
On differentiating w.r.t x, we get
f'(x) = 2cos x(-sin x) + cos x = cos x – sin2x
Put f'(x) = 0
cos x(1 – 2sin x) = 0
cos x = 0; sin x = 1/2
In x ϵ[0, π] if cos x = 0, then x = π/2
and if sin x = 1/2, then x = π/6 & 5π/6
Now, f”(x) = -sin x – 2 cos2x
f”(π/2) = -1 + 2 = 1 > 0
x = π/2 is a point of local minima f(π/2) = 1
f”(π/6) = ![]()
x = π/6 is a point of local maxima f(π/6) = 5/4
![]()
x = 5π/6 is a point of local minima f(5π/6) = 5/4
Global/Absolute maxima = ma{f(0), f(π/6), f(π)}
= max{1, 5/4, 1}
= 5/4 = Absolute maxima value
Global/Absolute minima = min{f(0), f(π/2), f(π/6), f(π)}
= min{1, 1, 5/4, 1}
= 1 = Absolute minima value
问题15:证明可以在半径为r的球体内刻出的最大体积的右圆锥的高度为4π/ 3
解决方案:
Let ABC be the cone
and o is the centre of the sphere.
AO = BO = CO = R
AO = h = height of cone
BD = CD = r = radius of cone.
∠DOC = θ -(Properties of circle)
In △ DOC,
OD = R cosθ & CD = Rsinθ,
r = R sin θ
AD = AO + OD = R + Rcosθ
h = R(1 + cosθ)
Now, the volume of the cone is
V = ![]()
v(θ) = ![]()
![]()
Put v(θ) = 0
sinθ[2cosθ + 2cos2θ − sin2θ] = 0
sinθ[2cosθ + 2cos2θ − 1] = 0
sinθ(3cosθ − 1)(1 + cosθ) = 0
sinθ = 0, cos = 1/3, cosθ = −1
If sinθ = 0, then volume will be 0.
If cosθ = -1, then sinθ = 0 & again volume will be 0.
But if cosθ = 1/3; sinθ = 2√2/3 and
Volume, v = 32/81πR3, which is maximum.
Height, h = R(1 + cosθ) = R(![]() )
)
h = 4r/3
Hence proved
问题16。令f是在[a,b]上定义的函数,对于所有x∈(a,b),f’(x)> 0。然后证明f是(a,b)上的一个递增函数。
解决方案:
Given that on [a, b] f'(x) > 0, for all x in interval I.
So let us considered x1, x2 belongs to I with x1 < x2
To prove: f(x) is increasing in (a, b)
According to the Lagrange’s Mean theorem
f(x2) – f(x1)/ x2 – x1 = f'(c)
f(x2) – f(x1) = f'(c)(x2 – x1)
Where x1 < c < x2
As we know that x1 < x2
so x1 < x2 > 0
It is given that f'(x) > 0
so, f'(c) > 0
Hence, f(x2) – f(x1) > 0
f(x2) < f(x1)
Therefore, for every pair of points x1, x2 belongs to I with x1 < x2
f(x2) < f(x1)
f(x) is strictly increasing in I
问题17:证明可以在半径为R的球体内切出的最大容积圆柱体的高度为2R /√3。另外,找到最大音量。
解决方案:
In △ABC,
AC2 = BC2 + AB2
4R2 = 4r2 + h2
r2 = R2–![]() ……….(1)
……….(1)
Now, volume of cylinder = πr2h
Put the value ov r2 from eq(1), we get
V = π(![]() ).h
).h
V(h) = ![]()
On differentiating both side we get
V ‘(h) = ![]()
Now, put V'(h) = 0
πR2 = ![]()
![]()
Now the maximum volume of cylinder = π[R2. 2R/√3 – 1/4.4R2/3.2R/√3]
= 4πR3/ 3√3
问题18。表明最大容积的圆柱体的高度(可以刻在高度为h和半垂直角α的右圆锥形中)是圆锥体的三分之一,最大圆柱体的体积为4/27 πH3个黄褐色2个α。
解决方案:
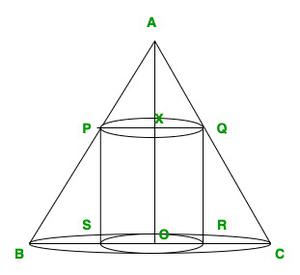
Let,
XQ = r
XO = h’
AO = h
OC = r’
∠XAQ = α
In triangle AXQ and AOC = XQ/OC = AX/AO
So, r’/r = h-h’/h
hr’ = r(h-h’)
hr’ = rh – rh’
rh’ = rh – hr’
rh’ = h(r – r’)
h’ = h(r – r’)/r
The volume of cylinder = πr’2h’
v = πr’2(h(r – r’)/r)
= π(h(rr’2 – r’3)/r)
On differentiating we get
v’ = πh/r(2rr’ – 3r’2)
Again on differentiating we get
v” = πh/r(2r – 6r’) ………(1)
Now put v’ = 0
πh/r(2rr’ – 3r’2) = 0
(2rr’ – 3r’2) = 0
2r’r = 3r’2
r’ = 2r/3
So, v is maximum at r’ = 2r/3
The maximum volume of cylinder = πh/r[r. 4r2/9 – 8r2/27]
= πhr2[4/27]
= 4/27πh(h tanα)2
= 4/27πh3 tan2α
问题19:一个半径为10 m的圆柱形罐正在以每小时314立方米的速度装满小麦。然后小麦的深度以
(A)1立方米/小时(B)0.1立方米/小时(C)1.1立方米/小时(D)0.5立方米/小时
解决方案:
Given,
Radius of cylinder = 10m [radius is fixed]
Rate of increase of volume = 314m3/h
ie dv/dt = 314m3/h
Now, the volume of cylinder = πr2h
v = π.(10)2.h
v = 100πh
On differentiating w.r.t t, we get
dv/dt = 100π![]()
![]()
![]()
So option A is correct
问题20.在点(2,-1)上,曲线x的切线的斜率x = t 2 + 3t – 8,y = 2t 2 – 2t – 5为
(A)22/7(B)6/7(C)7/6(D)-6/7
解决方案:
Given that the slope of the tangent to the curve x = t2 + 2t – 8 and y = 2t2 – 2t – 5
On differentiating we get
![]()
Now, when x = 2,
t2 + 3 – 8 = 2
t2 + 3 – 10 = 0
t2 – 2t + 5t – 10 = 0
(t – 2)(t + 5) = 0
Here, t = 2, t = -5 ……….(1)
When y = -1
2t2 – 2t – 5 = -1
2t2 – 2t – 4 = 0
t2 – t – 2 = 0
(t + 1)(t – 2) = 0
t = -1 or t = 2 ……….(2)
From eq(1) & eq(2) satisfies both,
Now, ![]()
![]()
So, option B is the correct.
问题21:如果m的值是y,则线y = mx +1是曲线y 2 = 4x的切线
(A)1(B)2(C)3(D)1/2
解决方案:
The curve if y2 = 4x …….(1)
On differentiating we get
![]()
![]()
The slope of the tangent to the given curve at point(x, y)
![]()
m = 2/y
y = 2/m
The equation of line is y = mx + 1
Now put the value of y, we get the value of x
2/m = mx + 1
x = 2 – m/m
Now put the value of y and x in eq(1), we get
(2/m)2 = 4(2 – m/m)
m = 1
Hence, the option A is correct
问题22。曲线2y + x 2 = 3上的点(1、1)的法线为
(A)x + y = 0(B)x – y = 0
(C)x + y +1 = 0(D)x – y = 1
解决方案:
The equation of curve 2y + x2 = 3
On differentiating w.r.t x, we get
2![]()
dy/dx = -x
The slope of the tangent to the given curve at point(1, 1)
dy/dx = -x = -1
m = -1
And slop of normal = 1
Now the equation of normal
(y -1) = 1(x – 1)
x – y = 0
So, B option is correct
问题23.曲线x 2 = 4y通过(1、2)的法线是
(A)x + y = 3(B)x – y = 3(C)x + y = 1(D)x – y = 1
解决方案:
The equation of curve is x2 = 4y …….(1)
On differentiating w.r.t x, we get
2x = ![]()
![]()
The slop of normal at (x, y)
-dx/dy = -2/x = m
The slop at given point(1, 2)
m = (y – 2)/(x – 1)
-2/x = (y – 2)/(x – 1)
y = 2/x
Now put the value of y in eq(1)
x2 = 4(2/x)
x = 2
and y = 1
So the point is (2, 1)
Now the slope of normal at point(2, 1) = -2/2 = -1
The equation of the normal is
(y – 1) = -1(x – 2)
x + y = 3
So option A is correct
问题24.曲线9y 2 = x 3上的点,曲线的法线与轴的交点相等,分别为
(一种) 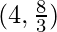 (B)
(B) 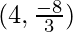
(C) 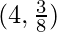 (D)
(D) 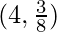
解决方案:
Given equation 9y2 = x3
On differentiating w.r.t x, we get
18y dy/dx = 3x2
dy/dx = 3x2/18y
dy/dx = x2/6y
Now, the slope of the normal to the given curve at point (x1, y1) is
![]()
Hence, the equation of the normal to the curve at point (x1, y1) is
![]()
![]()
![]()
![]()
According to the question it is given that the normal
make equal intercepts with the axes.
So,
![]()
![]() …………(1)
…………(1)
The point (x1, y1)lie on the curve,
![]() …………(2)
…………(2)
From eq(1) and (2), we get
![]()
From eq(2), we get
![]()
![]()
![]()
Hence, the required points are ![]()
So, option A is correct.