第12类NCERT解决方案–数学第I部分–第6章导数的应用–练习6.5 |套装2

问题13：找到两个数字，它们的总和为24，并且其乘积尽可能大。

解决方案：

Let us assume two numbers x and y.

Given that x + y = 24 ⇒ y = 24 – x

Now lets take a product function P(x) = x.y

Now put the value of y

P(x) = x.(24 – x)

P(x) = 24x – x²

Now, we have to maximize our product P(x).

Differentiating P(x) with respect to x, we get,  

$\frac{d}{dx}P(x)=24-2x$

Now put P'(x)=0

24 – 2x = 0

x = 12

y = 24 – x = 24-12

y = 12

Hence, the two numbers are 12 and 12 and the maximum product is 144.

问题14.找到两个正数x和y，使x + y = 60且xy ³最大。

解决方案：

Given that, 

x + y = 60 ⇒ x = 60 – y, x > 0, y > 0

Let’s take a function P(y) = xy³

P(x) = (60 – y)y³

P(x) = 60y³ – y⁹

On differentiating P(y) with respect to y, we get

P'(y) = 180y² – 4y³

Now put P'(y) = 0

180y² – 4y³ = 0

4y²(45 – y) = 0

y = 0 or y = 45

We doesn’t accept y = 0 because y > 0

So, y = 45

x = 60 – y = 60 – 45

x = 15

问题15.找到两个正数x和y，使它们的和为35，乘积x ² y ⁵为最大值。

解决方案：

Given that,

x + y = 35 ⇒ y = 35 – x 

Let us considered P(y) = x²y⁵  

Put the value of y from the above equation

P(x) = x²(35 – x)⁵

On differentiating P(x) with respect to y, we get,

P'(x) = x²5(35 – x)⁴(-1) +(35 – x)⁵2x

P'(y) = x(35 – x)⁴[-5x + (35 -x)2]

P'(y) = 7x(35 – x)⁴(10 – x)

Now put P'(x) = 0

7x(35 – x)⁴(10 – x) = 0

x = 0 or x = 35 or x = 10

Here, x = 0 is rejected because x is positive, x = 35 is also rejected because 

y = 35 – 35 = 0, but y is positive. So, x = 10 is the turning point.

Now we do second derivative test

P”(x) = 7(35 – x)³(6x² – 120x +350)

Now put x = 10

we get

P”(x) = 7(35 – 10)³(6 x 100 – 120 x 10 +350)

= 7(25)³(250) < 0

So by second derivative test p'(x) will be maximum at x = 10. So, y = 25

问题16。找到两个正数，其和为61，且其立方的和为最小值。

解决方案：

Let us considered two numbers a and y

x + y = 16 ⇒ y = 16 – x

Sum of cubes = x³ + y³ 

So let us considered s(x) = x³ + y³ 

S(x) = x³ + (16 – x)³

S(x) = x³ + 16³ – x³ – 3.16.x(16 – x)

S(x) = 16³ – x.16².3 + 3.16.x²

S'(x) = 2.3.16x – 3.16²

Now put S'(x) = 0

2.3.16.x = 3.16²

2.x = 16

x = 8

So at x = 8 S”(x) = 96(positive), so x = 8 is a local minima point. Hence

y = 16 – x = 8

The two numbers are 8 and 8 and the sum of cubes is 8³ + 8³ = 1024

问题17：将一块方形的，边长为18cm的锡罐制成一个没有顶部的盒子，方法是从每个角上切一个正方形，然后将折翼折叠起来以形成盒子。应该切掉正方形的一面是什么，以使盒子的体积最大。

解决方案：

The dotted square will be the base of the open cuboid.

Side will be 18 – 2x

The cuboid will now have dimensions 18 – 2x, 18 – 2x, x

Volume of the open box,

V(x) = (18 – 2x).(18 – 2x).x

V(x) = x(18 – 2x)²

Now we have to maximize V(x),

Now put V'(x) = 0

V'(x) = 2(18 – 2x).x(-2) + (18 – 2x)² = 0

(18 – 2x)[-4x + 18 – 2x] = 0

(18 – 2x)(18 – 6x) = 0

x = 9 and x = 3

Now put x = 9

V(x) = (18 – 2x)².x

V(9) = (18 – 2 x 9)².9

V(9) = 0

It is impossible so we doesn’t accept x = 9

Now put x = 3

V(x) = (18 – 2x)².x

V(3) = (18 – 2 x 3)².3

V(3) = 432

So, x = 9 is the turning point

Hence at x = 9, V”(x) = -72(negative), So, volume is minimum at x = 3. 

Now, the sides of the square for maximum volume is 3.   

问题18.将一块矩形的锡纸(45厘米乘24厘米)切成一个没有顶部的盒子，方法是切掉每个角部的正方形并折叠襟翼。正方形的哪一面应被切除，以使盒子的体积最大?

解决方案：

Given,

A rectangular sheet of dimension 45 x 24. Lets the side of the wall square be x,

Then the cuboid have its base as the blue rectangle and height equal to side of the square.

The dimensions of the cuboid will be 45 – 2x, 24 – 2x and x.

Let V(x) = Volume function, so

V(x) = (45 – 2x)(24 – 2x)(x)

V(x) = (45x – 2x²)(24 – 2x)

V'(x) = (45x – 2x²)(-2) + (24 – 2x)(45 – 4x)

Now put V'(x) = 0

(45x – 2x²).2 = 2(12 – x)(45 – 4x)

45x – 4x² = 12.45 – 48x – 45x + 4x²

6x² – 138x + 12.45 = 0

x² – 23x + 90 = 0

(x – 18)(x – 5) = 0

x = 18 or x = 5

x can’t be equal to 18, 24 – 2x will become negative. Hence x = 5 is the turning point. 

Now, volume is V(x) = (45 – 2x)(24 – 2x)(x)

Now put x = 5, V = (45 – 10).(24 – 10).(5)

V = 35.12.5

V = 2100

Side of small square is 5cm

问题19：证明在一个给定的固定圆中所有内接的矩形中，正方形具有最大面积。

解决方案：

Given, a variable rectangle inside a fixed circle.

Let the diameter of the fixed circle be equal to d and the 

sides of the rectangle be equal to x and y 

Now, the diameter d is fixed.

Let the area function be A(x) = x.y

From the triangle ABC,

AB² + BC² = AC²

x² + y² = (2a)²

y² = (2a)² – x²

y = $\sqrt{(2a)^2-x^2}$

Now, A(x) = x.y = x.$\sqrt{(2a)^2-x^2}$

A'(x) = x.$\frac{1}{2\sqrt{(2a)^2-x^2}}x-2x+\sqrt{(2a)^2-x^2}$

A'(x) = $\frac{4a^2-2x^2}{\sqrt{4a^2-x^2}}$

Now we find the second derivative

A”(x) = 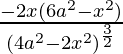$\frac{-2x(6a^2-x^2)}{(4a^2-2x^2)^{\frac{3}{2}}}$

Now put A'(x) = 0 for maximum and minimum values.

A'(x) = $\frac{4a^2-2x^2}{\sqrt{4a^2-x^2}}$ = 0

x = √2a

When x = √2a, 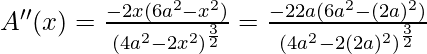$A''(x) = \frac{-2x(6a^2-x^2)}{(4a^2-2x^2)^{\frac{3}{2}}} = \frac{-2√2a(6a^2-(√2a)^2)}{(4a^2-2(√2a)^2)^{\frac{3}{2}}}$ = -4(negative)

So, at x = √2a the area of rectangle is maximum hence, y = √2a 

问题20：证明给定表面和最大体积的右圆柱应使其高度等于基座的直径。

解决方案：

Given,

A right circular cylinder of given surface area.

Now, let the total surface are be A.

A = 2πr(r + h)

A/2π = r² + rh

Let us assume A/2π = M

h = M – r²/r

Now the volume of the cylinder V(r) = πr²h

So, V(r) = πr²(M – r²/r)

= π(rM – r³)

V'(r) = π(M – 3r²)

and V”(r) = -π(6r)

Now put V'(r) = 0

π(rM – r³) =0

r = √M/3

At r = √M/3, V”(r) = -π(6√M/3) is negative, so r is maximum at √M/3. 

Hence, h = 2r

Clearly, the height is equal to the diameter of the base.

问题21.在给定体积为100立方厘米的所有封闭的圆柱形罐(直圆形)中，找到具有最大表面积的罐的尺寸吗?

解决方案：

Given: cylindrical can of fixed volume = 100 cc.

Find: the dimensions of the can 

As we know that

Volume = πr²h = 100cc

h = 100/πr²             ————-(1)

Now, the total surface area(A) = 2πr² + 2πrh

A = 2πr² + 2πr(100/πr²)

A = 2πr² + (200/r)

A'(r) = 4πr + (200/r²)

Now we find

A”(r) = 4π+ (200/r³)

Now put A'(r) = 0

A'(r) = 4πr + (200/r²) = 0

r = (50/π)^1/3

At r = (50/π)^1/3, A”(r) = 4π+ (200/((50/π)^1/3)³) = 12π is positive. 

So, area is minimum when r = (50/π)^1/3.

Hence, the height is (h) = 100/π((50/π)^1/3)² = 2.(50/π)^1/3 = 2r

问题22.长度为28m的电线应切成两段。一件被制成正方形，另一件被制成圆形。两件的长度应为多少，以使正方形和圆形的总面积最小?

解决方案：

Given that the length of the wire is 8 and cut into two pieces. From one 

piece a square is formed and form another piece a circle is formed. so let 

us assume x be the side of square and y be the radius of circle. 

So, Length of the wire = Perimeter(of square) + circumference(of circle)

28 = 4x + 2πy

y = (14 – 2x)/π

As we know that the area of circle is πy² and the area of square is x²

So, total area(A) = πy² + x²

Now put the value of y we get

A = π((14 – 2x)/π)² + x²

A'(x) = 2x – 8/π(7 – x)

and 

A”(x) = 2 + 8/π

Now put A'(x) = 0

2x – 8/π(7 – x) = 0

x = 28/π + 4

So, at point x = 28/π + 4, area is minimum because A”(x) is positive. 

Hence, the wire cut at distance 28/π + 4 

问题23.证明半径为R的球体中可以接切的最大圆锥体的体积为球体体积的8/27。

解决方案：

According to the question it is given that the sphere contains a cone. 

So let us assume that the center of the sphere is O, the radius of the sphere is R and UV = x and SV = y.

So in triangle OVU

OV² + VU ²= OU²

(y – R)² + x² = R²

x² = 2Ry – y² …(1)

So, the volume of the cone(V) = 1/3πx²y

Now put the vlaue of x from eq(1)

= 1/3π(2Ry – y²)y

V = 1/3π(2Ry² – y³)

V'(y) = 1/3π(4Ry – 3y²)

and 

V”(y) = 1/3π(4R – 6y)

Now put V'(y) = 0

1/3π(4Ry – 3y²) = 0

y = 4R/3

So, at y = 4R/3, V”(y) = 1/3π(4R – 6y) = 1/3π(4R – 6(4R/3)) = -4R/3 is negative. 

So, Volume is maximum at y = 4R/3.

Now put the value of y in eq(1), we get

x² = 2R(4R/3) – (4R/3)² 

x = 8R²/9

So the maximum volume of the cone is 

V = 1/3πx²y

V = 1/3π(8R²/9)²(4R/3) = 8/27

问题24.证明最小曲面和给定体积的右圆锥的高度等于基部半径的√2倍。

解决方案：

Let us considered r be the radius of the cone and h be the height of the cone.

So, the volume of the cone(V) = 1/3πr²h

r²h = 3V/π

r² = M/h [3V/π = M] ….(1)

As we know that the surface area of the cone:

(A) = $\pi r\sqrt{r^2+h^2}$

(A)² = π²r² (r² + h²)

Now put the value of r² from above

(A)² = S = π²M/h (M/h + h²)

= π²M(M/h² + h)

So, S'(h) = π²M(-2Mh^-3 + 1) and

S”(h) = π²M(6Mh^-4) 

Now put S'(h) = 0

π²M(-2Mh^-3 + 1) = 0

h = (2M)^1/3

So at h = (2M)^1/3, S”(h) = π²M(6Mh^-4) = 6π²M²/(2M)^4/3 is positive. 

So, area is minimum at h = (2M)^1/3

So, r = M/(2M)^1/3

From eq(1), we get

h = √2r

问题25表明，该最大容积的锥形的和给定的倾斜高度的半垂直角为tan ^-1√2。

解决方案：

Let us assume r be the radius, h be the height, l be the slant height, and θ be the semi vertical angle of cone. 

So, 

l ² = r²+ h²

r² = l² – h²  ….(1)

As we know that the volume of the cone is 

V = 1/3πr²h

Now put the value of r² from eq(1)

V = 1/3π(l² – h²)h

V = 1/3π(hl² – h³)

So, V'(h) = 1/3π(l² – 3h²) and 

V”(h) = 1/3π(- 6h) = -2πh

Now put V'(h) = 0

1/3π(l² – 3h²) = 0

h = l/√3

So, at h = l/√3, V”(h) = -2πh = -2π(l/√3) is negative so, V is maximum at h = l/√3

So from eq(1), we get

r² = l² – (l/√3)²

r = √2(l/√3)

As we know that the semi vertical angle is tan θ = r/h = √2(l/√3)/l/√3 = √2. So the value of θ = tan^-1√2

问题26：证明给定表面积和最大体积的右圆锥的半垂直角为sin ^-1 (1/3)。

解决方案：

Let us assume r be the radius, h be the height, and θ be the semi vertical angle of cone. 

So, the total surface area (A) = $\pi r\sqrt{r^2+h^2}+ \pi r^2$

$r\sqrt{r^2+h^2}+ r^2$= A/π

$r\sqrt{r^2+h^2}+ r^2$= S

$r\sqrt{r^2+h^2}$ = S – r²

On squaring on both side we get

r²(r² + h²) = (S – r²)²

r² = S²/h² + 2S² ….(1)

As we know that the volume of the cone is 

V = 1/3πr²h

Now put the value of r, we get

V = 1/3π(S²/h² + 2S²)h

V = 1/3πS²(h/h² + 2S)

Now 

V'(h) = 1/3πS²(2S – h²)/(h + 2S)²

Now put V'(h) = 0

 1/3πS²(2S – h²)/(h + 2S)² = 0

h = +-√2S

Here, the h = √2S is a valid value and h = -√2S is not valid because height can’t be negative. So, h = √2S is the turning point. 

V'(h) > 0, so the volume is maximum at h = √2S. 

So put the value of h = √2S in eq(1), we get

r = √S/2

and as we know that the semi vertical angle is sin θ = r/√r ²+ h². So the value of θ = tan^-11/3

问题27.曲线x ² = 2y上最接近点(0,5)的点是

(A)(2，√2，4)(B)(2，√2，0)(C)(0，0)(D)(2，2)

解决方案：

Given that, x² = 2y

Let any random point on this curve be (h, k)

So, h² = 2k; k = h²/2

The random point is (h, h²/2)

Minimizing the distance

d² = (h – 0)² + ($\frac{h^2}{2}-5$) 

d² = f(x) = h² + $(\frac{h^2}{2}-5)$

f'(x) = 2h + 2$( \frac{h^2}{2}-5)$.h

Now put f'(h) = 0

2h[1+$\frac{h^2}{2}-5$] = 0

h = 0 or $\frac{h^2}{2}-4=0$

h = 0 or h = 2√2​, h =−2√2​

If h = 0, d=$\sqrt{h^2+(\frac{h^2}{2}-5)^2}=5$

If h = ±2√2,

$\space d=\sqrt{8+(4-5)^2}=3\\$

So, h = ±2√2       [giving minimum distance]

k = h2/2 = 8/2 = 4

Points are (±2√2, 4)

So the correct option is A

问题28.对于x的所有实数值，x的最小值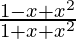$\frac{1-x+x^2}{1+x+x^2}$

(A)0(B)1(C)3(D)1/3

解决方案：

Given that, $f(x)=\frac{1-x+x^2}{1+x+x^2}$

$f'(x)=\frac{-2(1-x^2)}{(1+x+x^2)^2}$

 Now put f'(x) = 0

1 + x + x² – 2x² – x = 0

x² = 1

x = ±1 

So, x = -1, x = 1 are the turning points

Now let us find the value of f(x) at points x = -1, x = 1

Put x = 1

$f(1)=\frac{1-1+1^2}{1+1+1^2}$

f(1) = 1/3

Put x = -1

$f(-1)=\frac{1+1+1^2}{1-1+1^2}$

f(-1) = 3

Hence, the maximum value of $f(x)=\frac{1-x+x^2}{1+x+x^2}$ is 1/3

So the correct option is D

问题29. [x(x – 1)+1] ^1/3的最大值，0≤x≤1为

(A)(1/3) ^1/3 (B)1/2(C)1(D)0

解决方案：

Given that,

f(x) = [x(x – 1) + 1]^1/3 = (x² – x + 1)^1/3, x ϵ [0, 1]

f′(x) = 1/3​(x² − x + 1)^-2/3 ​.(2x−1)

or we can write as

 $f'(x)=\frac{2x-1}{3(x^2-x+1)^\frac{2}{3}}$

Now put f'(x) = 0

$f'(x)=\frac{2x-1}{3(x^2-x+1)^\frac{2}{3}} = 0$

2x – 1 = 0

So, x = 1/2 is the turning point which belongs to the given closed interval 0 ≤ x ≤ 1. 

Now let us find the value of f(x) at points x = 1/2, x = 0, x = 1

Put x = 1/2

f(1/2) = (1/4 – 1/2 + 1)^1/3

f(1/2) = (3/4)^1/3 < 1

Put x = 1

f(1) = (1 – 1 + 1)^1/3

f(1) = 1

Put x = 0

f(0) = (0 – 0 + 1)^1/3

f(0) = 1

Hence, the maximum value of [x(x – 1) + 1]^1/3 is 1

So the correct option is C