第 12 类 RD Sharma 解决方案 - 第 6 章行列式练习前。 6.6 |设置 2

问题 19. 令 A = [a _ij ] 为 3 × 3 阶方阵，C _ij表示 a _ij在 A 中的辅因子。如果 |A| = 5，求 a ₁₁ C ₂₁ + a ₁₂ C ₂₂ + a ₁₃ C ₂₃的值。

解决方案：

As we know that, if a matrix is square matrix of order n, then the sum of the products of elements of a row or a column with the cofactors of the corresponding elements of some other row or column is zero. 

So, 

A = [a_ij] is a square matrix of order n.

Also we have,

$\sum^n_{j = 1} a_{i j} C_{k j} = 0$

And $\sum^n_{i = 1} a_{i j} C_{i k} = 0$

=> a₁₁ C₂₁ + a₁₂ C₂₂ + a₁₃ C₂₃ = 0 

Therefore, the required value is 0.

问题 20. 找出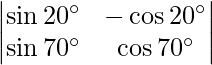$\begin{vmatrix}\sin 20^\circ & - \cos 20^\circ\\ \sin 70^\circ& \cos 70^\circ\end{vmatrix}$ .

解决方案：

Given that, 

A = 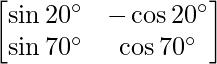$\begin{bma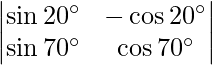trix} \sin 20^\circ & - \cos 20^\circ\\\sin 70^\circ & \cos 70^\circ \end{bmatrix}$ 

=> |A| = $\begin{vmatrix} \sin 20^\circ & - \cos 20^\circ\\\sin 70^\circ & \cos 70^\circ \end{vmatrix}$

= sin 20° cos 70° + cos 20° sin 70°

= sin (20° + 70°)

= sin 90

= 1

问题 21. 如果 A 是一个满足 A ^T A = I 的方阵，写出 |A| 的值。

解决方案：

Let us assume that A = [a_ij] be a square matrix of order n.

So, by using the property of determinants, we get

=> |A| = |A^T|

Here, we have

=> A^T A = I

=> |A^T A| = 1

So, the determinants are of same order, we get

=> |A^T A| = |A^T| |A|

=> |A^T| |A| = 1

=> $\left| A \right| = \frac{1}{\left| A^T \right|}$

=> $\left| A \right| = \frac{1}{\left| A \right|}$

=> |A|² = 1

=> |A| = ±1

Therefore, the value of |A| is ±1.

问题 22. 如果 A 和 B 是相同阶的方阵，使得 |A| = 3 且 AB = I，然后写出 |B| 的值。

解决方案：

According to the question, A and B are square matrices of the same order.

So, by using the property of determinants we get,

=> |AB| = |A| |B|

Here, |A| = 3, AB = I.

=> |AB| = 1

=> |A| |B| = 1

=> 3 |B| = 1

=> |B| = 1/3

Therefore, the value of |B| is 1/3.

问题 23. A 是 3 阶斜对称，写出 |A| 的值。

解决方案：

Here, |A| = 4.

So we have,

Order of the matrix (n) = 3

Using the properties of matrices, we get

For a square matrix of order n and constant k, we know,

=> |k A| = kⁿ |A|

=> |- A| = (-1)³ |A|

= (-1) (4)

= -4

Therefore, the value of |A| is -4.

问题 24. 如果 A 是行列式为 4 的 3 阶方阵，则写出 |−A| 的值。

解决方案：

Given that, |A| = 4.

Order of the matrix (n) = 3

So, by using the properties of matrices, we get

=> |k A| = kⁿ |A|

=> |- A| = (-1)³ |A|

= (-1) (4)

= -4

Therefore, the value of |A| is -4.

问题 25. 如果 A 是一个方阵，使得 |A| = 2，写出| ^{A T} |的值。

解决方案：

Given that, |A| = 2

As we know that in a square matrix, |A| = A^T

So, they are of sane order 

Hence, |A A^T| = |A| |A^T|

=> |A A^T| = 2 (2)

= 4

Therefore, the value of |A A^T| is 4.

问题 26. 求行列式的值$\begin{vmatrix}243 & 156 & 300 \\ 81 & 52 & 100 \\ - 3 & 0 & 4\end{vmatrix}$ .

解决方案：

Given that, 

A = 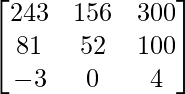$\begin{bmatrix}243 & 156 & 300 \\ 81 & 52 & 100 \\ - 3 & 0 & 4\end{bmatrix}$

|A| = $\begin{vmatrix}243 & 156 & 300 \\ 81 & 52 & 100 \\ - 3 & 0 & 4\end{vmatrix}$

On applying R₁ -> R₁ – 3R₂ we have,

= $\begin{vmatrix} 243 - \left( 81 \times 3 \right) & 156 - \left( 52 \times 3 \right) & 300 - \left( 100 \times 3 \right)\\ 81 & 52 & 100\\ - 3 & 0 & 4 \end{vmatrix}$

= $\begin{vmatrix} 0 & 0 & 0\\ 81 & 52 & 100\\ - 3 & 0 & 4 \end{vmatrix}$  

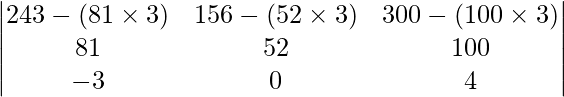
= 0

Therefore, the value of the determinant is 0.

问题 27. 求行列式的值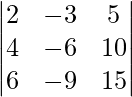$\begin{vmatrix}2 & - 3 & 5 \\ 4 & - 6 & 10 \\ 6 & - 9 & 15\end{vmatrix}$ .

解决方案：

Given that, 

A = 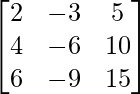$\begin{bma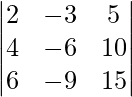trix}2 & - 3 & 5 \\ 4 & - 6 & 10 \\ 6 & - 9 & 15\end{bmatrix}$

|A| = $\begin{vmatrix} 2 & - 3 & 5\\4 & - 6 & 10\\6 & - 9 & 15 \end{vmatrix}$

On applying R₂ -> R₂ – 2R₁ we get,

= $\begin{vmatrix} 2 & - 3 & 5\\4 - 4 & - 6 + 6 & 10 - 10\\6 & - 9 & 15 \end{vmatrix}$

= $\begin{vmatrix} 2 & - 3 & 5\\0 & 0 & 0\\6 & - 9 & 15 \end{vmatrix}$

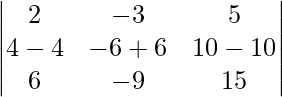
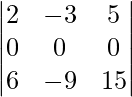
= 0

Therefore, the value of the determinant is 0.

问题 28. 如果矩阵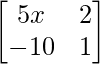$\begin{bmatrix}5x & 2 \\ - 10 & 1\end{bmatrix}$是奇异的，求 x 的值。

解决方案：

As we know that a matrix is singular only when its determinant is zero. 

According to the question, 

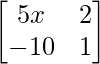$\begin{bmatrix}5x & 2 \\ - 10 & 1\end{bmatrix}$ is a singular matrix

So, 

=> |A| = 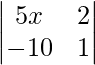$\begin{vmatrix} 5x & 2 \\- 10 & 1 \end{vmatrix}$ = 0

On expanding the determinant we get,

=> 5x + 20 = 0 

=> x = -20/5

=> x = -4

Therefore, the value of x is -4.

问题 29. 如果 A 是 n × n 阶方阵，使得 |A| = λ，然后写出 |−A| 的值。

解决方案：

Given that,

A is a square matrix of order n × n

So, |A| = λ

=> |- A| = (-1)ⁿ A

=> |-A| = (-1)ⁿ λ

Therefore, the value of |-A| is (-1)ⁿ λ.

问题 30. 求行列式的值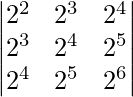$\begin{vmatrix}2^2 & 2^3 & 2^4 \\ 2^3 & 2^4 & 2^5 \\ 2^4 & 2^5 & 2^6\end{vmatrix}$ .

解决方案：

Given that, 

A = 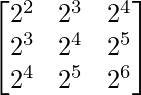$\begin{bmatrix}2^2 & 2^3 & 2^4 \\ 2^3 & 2^4 & 2^5 \\ 2^4 & 2^5 & 2^6\end{bmatrix}$

|A| = $\begin{vmatrix}2^2 & 2^3 & 2^4 \\ 2^3 & 2^4 & 2^5 \\ 2^4 & 2^5 & 2^6\end{vmatrix}$ 

On taking out common factors from R₁, R₂ and R₃ we get,

= $2^2 \times 2^3 \times 2^4 \begin{vmatrix} 1 & 2 & 2^2 \\1 & 2 & 2^2 \\1 & 2 & 2^2 \end{vmatrix}$

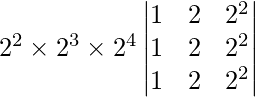
Here, the two rows are identical, so we get

= $2^2 \times 2^3 \times 2^4 \times 2 \begin{vmatrix} 1 & 1 & 2^2 \\1 & 1 & 2^2 \\1 & 1 & 2^2 \end{vmatrix}$

= 0 

Therefore, the value of the determinant is 0.

问题 31. 如果 A 和 B 是同阶的非奇异矩阵，证明 AB 是奇异的还是非奇异的。

解决方案：

According to the question, A and B be non-singular matrices of order n.  

Here, |A| ≠ 0 and |B| ≠ 0. 

So, the order of these matrix are same, we get

=> |AB| = |A| |B|

=> |AB| = 0 if |A| = 0 or |B| = 0

But as it is not the case here, so |AB| is non- zero matrix and AB is non-singular matrix.

Hence proved.

问题 32. 3 × 3 阶矩阵的行列式为 2。|A (3I)| 的值是多少，其中 I 是 3 × 3 阶单位矩阵。

解决方案：

Given that a matrix of order 3 x 3 has determinant 2. 

So let us assume B be the matrix. so the order of the matrix is 3

and |B| = 2  

Let us consider I be the identity matrix, so we get

=> |I| = 1 

=> 3 |I| = 3

=> |A (3I)| = |3 A|

= 3³ |A|

= 27 (2)

= 54

=> |A (3I)| = 54

Therefore, the value of |A (3I)| is 54.

问题 33. 如果 A 和 B 是 3 阶方阵，使得 |A| = -1，|B| = 3，则求 |3 AB| 的值。

解决方案：

We have,

A and B are square matrices of order 3.

Also |A| = −1, |B| = 3.

We know,

As n is the order of A, we get

=> |K A| = Kⁿ |A| 

=> |3 AB| = 3³ |AB|  

If the order of A and B matrix are same and they are square matrix then |AB| = |A| |B|. 

So, we have,

=> |3 AB| = 3³ |A| |B|

= 27 (-1) (3)

= -81

Therefore, the value of |3 AB| is -81.

问题 34. 写出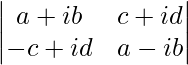$\begin{vmatrix}a + ib & c + id \\ - c + id & a - ib\end{vmatrix}$ .

解决方案：

We have,

A = 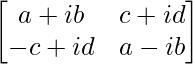$\begin{bmatrix}a + ib & c + id \\ - c + id & a - ib\end{bmatrix}$

|A| = $\begin{vmatrix}a + ib & c + id \\ - c + id & a - ib\end{vmatrix}$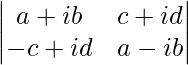

= a² – iab + iab – i² b² – (-c² – icd + icd + i² d²) 

= a² – i² b² + c² – i² d²  

Here, we have, i² = – 1.

So we get,  

|A| = a² – (-1) b² + c² – (-1) d²  

= a² + b² + c² + d²

Therefore, the value is a² + b² + c² + d².

问题 35. 在下面的矩阵中写出₁₂的辅因子$\begin{bmatrix}2 & - 3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & - 7\end{bmatrix}$ .

解决方案：

We have

$\begin{bmatrix}2 & - 3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & - 7\end{bmatrix}$

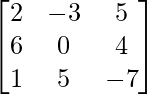
So,

=> a₁₂ = -3

Now we find the cofactor of a₁₂ 

a₁₂ = (-1)¹⁺² 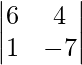$\begin{vmatrix}6 & 4 \\ 1 & - 7\end{vmatrix}$

= – (- 42 – 4) 

= 46

Therefore, the value of the required cofactor is 46.

问题 36. 如果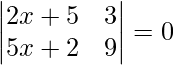$\begin{vmatrix}2x + 5 & 3 \\ 5x + 2 & 9\end{vmatrix} = 0$ , 找到 x。

解决方案：

Here we have,

A = 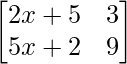$\begin{bma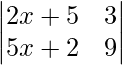trix}2x + 5 & 3 \\ 5x + 2 & 9\end{bmatrix}$

=> |A| = $\begin{vmatrix}2x + 5 & 3 \\ 5x + 2 & 9\end{vmatrix}$ = 0

=> 9(2x + 5) – 3(5x + 2) = 0

=> 18x + 45 – 15x – 6 = 0  

=> 3x + 39 = 0

=> 3x = – 39 

=> x = -39/3 

=> x = -13

Therefore, the value of x is -13.

问题 37. 从以下找到 x 的值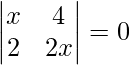： $\begin{vmatrix}x & 4 \\ 2 & 2x\end{vmatrix} = 0$

解决方案：

We have,

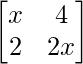
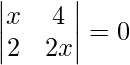
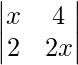A = $\begin{bmatrix}x & 4 \\ 2 & 2x\end{bmatrix}$

|A| = $\begin{vmatrix}x & 4 \\ 2 & 2x\end{vmatrix} = 0$

=> $\begin{vmatrix}x & 4 \\ 2 & 2x\end{vmatrix}$ = 0 

=> 2 x² – 8 = 0 

=> 2 x² = 8

=> x² = 8/2

=> x² = 4  

=> x = √4

=> x = ±2

Therefore, the value of x is ±2.