第 12 类 RD Sharma 解决方案 - 第 6 章行列式 - 练习 6.2 |设置 2
证明下列恒等式:
问题 18。  = -2
= -2
解决方案:
Considering the determinant, we have
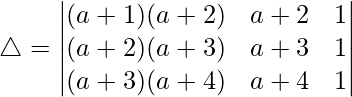
R2⇢R2 – R1 and R3⇢R3 – R2
![Rendered by QuickLaTeX.com \triangle = \begin{vmatrix}(a+1)(a+2) & a+2 & 1 \\ (a+2)(a+3)-(a+1)(a+2) & a+3-(a+2) & 0 \\ (a+3)(a+4)-(a+2)(a+3) & a+4-(a+3) & 0 \end{vmatrix}\\ \triangle = \begin{vmatrix}(a+1)(a+2) & a+2 & 1 \\ (a+2)[a+3-a-1] & a+3-a-2 & 0 \\ (a+3)[a+4-a-2] & a+4-a-3 & 0 \end{vmatrix}\\ \triangle = \begin{vmatrix}(a+1)(a+2) & a+2 & 1 \\ 2(a+2) & 1 & 0 \\ 2(a+3) & 1 & 0 \end{vmatrix}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_6_Determinants_%E2%80%93_Exercise_6.2_%7C_Set_2_2.jpg)
△ = 1[2(a + 2) – 2(a + 3)]
△ = (4a + 4 – (4a + 6))
△ = (4a + 4 – 4a – 6)
△ = -2
Hence proved
问题 19。 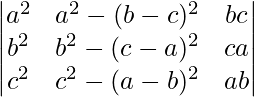 = (a – b)(b – c)(c – a)(a + b + c)(a 2 + b 2 + c 2 )
= (a – b)(b – c)(c – a)(a + b + c)(a 2 + b 2 + c 2 )
解决方案:
Considering the determinant, we have
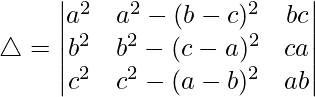
C2⇢C2 – 2C1 – 2C3

Taking -(a2 + b2 + c2) common from C2, we get
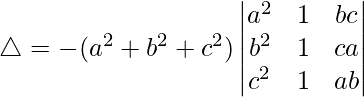
R2⇢R2 – R1 and R3⇢R3 – R1
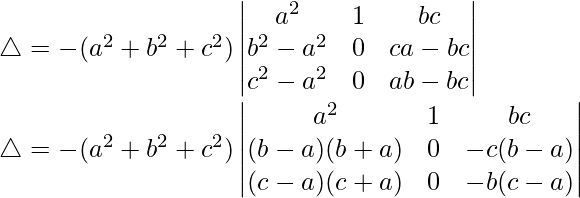
Taking (b – a) and (c – a) common from R1 and R2, we get
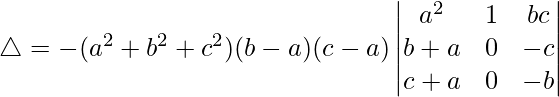
△ = -(a2 + b2 + c2)(b – a)(c – a)[1((-b)(b + a) – (c + a)(-c))]
△ = (a2 + b2 + c2)(a – b)(c – a)[(-b)(b + a) + (c + a)c]
△ = (a2 + b2 + c2)(a – b)(c – a)[-b2 – ab + ac + c2]
△ = (a2 + b2 + c2)(a – b)(c – a)
△ = (a2 + b2 + c2)(a – b)(c – a)[(c – b)(c + b) + a(c – b)]
△ = (a2 + b2 + c2)(a – b)(c – a)(c – b)
△ = (a2 + b2 + c2)(a + b + c)(a – b)(b – c)(c – a)
Hence proved
问题 20。  = (a – b)(b – c)(c – a)(a 2 + b 2 + c 2 )
= (a – b)(b – c)(c – a)(a 2 + b 2 + c 2 )
解决方案:
Considering the determinant, we have
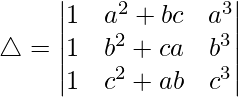
R2⇢R2 – R1 and R3⇢R3 – R1
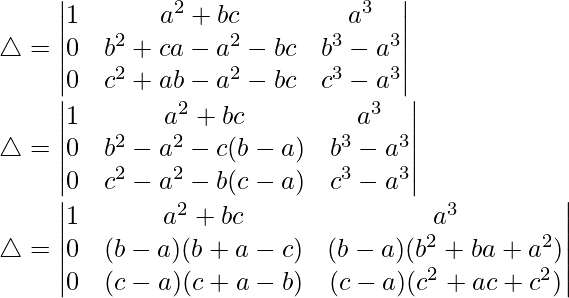
Taking (b – a) and (c – a) common from R2 and R3 respectively, we get
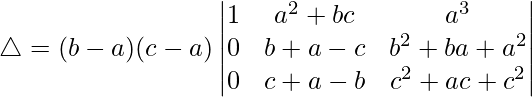
△ = (b – a)(c – a)[1((b + a – c)(c2 + a2 + ac) – (c + a – b)(b2 + a2 + ab))]
△ = (b – a)(c – a)(b – c)(a + b + c)
△ = -(a – b)(c – a)(b – c)(a + b + c)
Hence proved
问题 21。 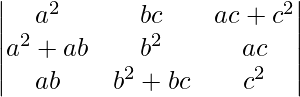 = 4a 2 b 2 c 2
= 4a 2 b 2 c 2
解决方案:
Considering the determinant, we have

Taking a, b and c common from C1, C2 and C3 we get
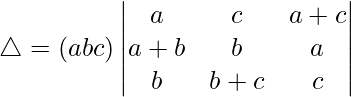
C1⇢C1 + C2 + C3
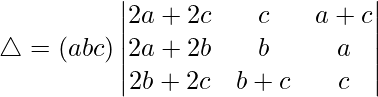
Taking 2 common from C1, we get
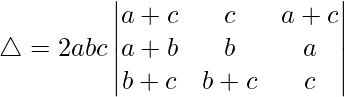
C2⇢C2 – C1 and C3⇢C3 – C1
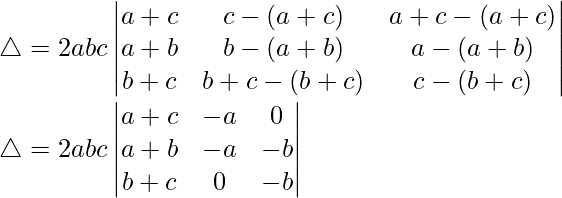
C1⇢C1 + C2 + C3
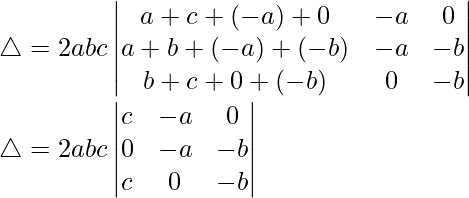
Taking c, a and b common from C1, C2 and C3 we get
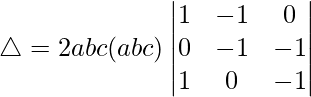
R3⇢R3 – R1
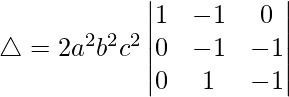
△ = 2a2b2c2[1((-1)(-1) – (-1)(1))]
△ = 2a2b2c2[1 – (-1)]
△ = 2a2b2c2[1 + 1]
△ = 4a2b2c2
Hence proved
问题 22。 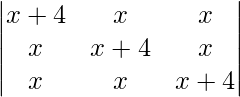 = 16(3x + 4)
= 16(3x + 4)
解决方案:
Considering the determinant, we have
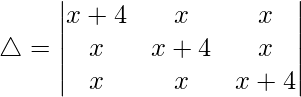
C1⇢C1 + C2 + C3
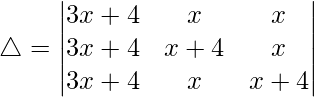
Taking (3x + 4) common from C1, we get
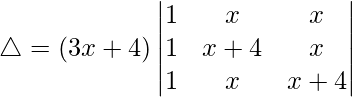
R2⇢R2 – R1 and R3⇢R3 – R1
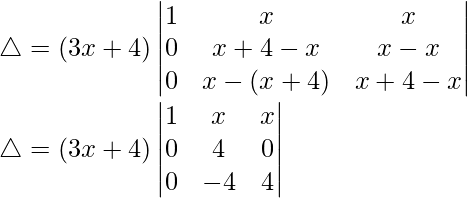
△ = (3x + 4)[1((4)(4) – (-4)(0))]
△ = (3x + 4)[16 – 0]
△ = 16(3x + 4)
Hence proved
问题 23。 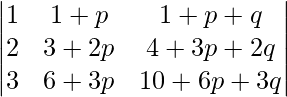 = 1
= 1
解决方案:
Considering the determinant, we have
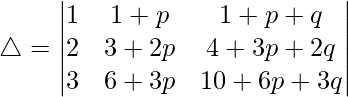
C2⇢C2 – pC1 and C3⇢C3 – qC1
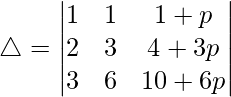
C3⇢C3 – pC2
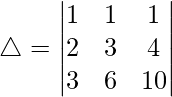
C2⇢C2 – C1 and C3⇢C3 – C2
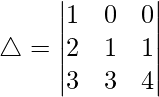
△ = 1[(1)(4) – (1)(3)]
△ = [4 – 3]
△ = 1
Hence proved
问题 24。 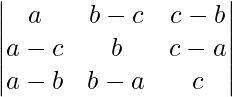 = (a + b – c)(b + c – a)(c + a – b)
= (a + b – c)(b + c – a)(c + a – b)
解决方案:
Considering the determinant, we have
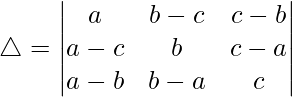
R1⇢R1 – R2 – R3
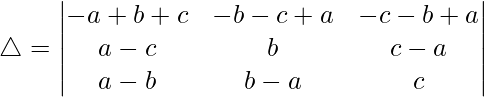
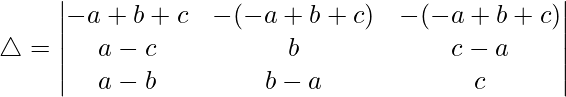
Taking (-a+b+c) common from R1, we get
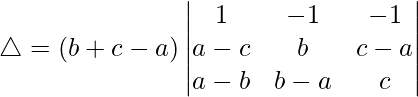
C2⇢C2 + C1 and C3⇢C3 + C1
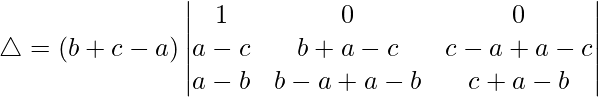
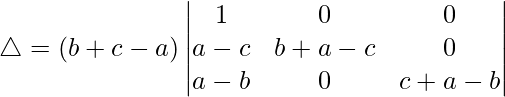
△ = (b + c – a)[1((b + a – c)(c + a – b) – (0)(0))]
△ = (b + c – a)[(b + a – c)(c + a – b)]
△ = (b + c – a)(b + a – c)(c + a – b)
Hence proved
问题 25。 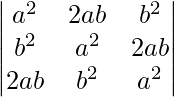 = (a 3 + b 3 ) 2
= (a 3 + b 3 ) 2
解决方案:
Considering the determinant, we have

C1⇢C1 + C2 + C3
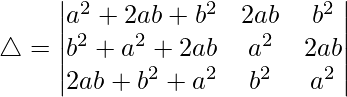
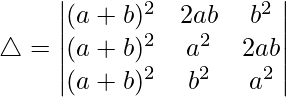
Taking (a + b)2 common from C1, we get
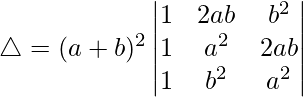
R2⇢R2 – R1 and R3⇢R3 – R1
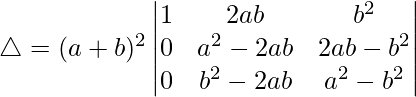
R2⇢R2 – R3
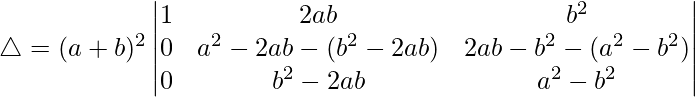
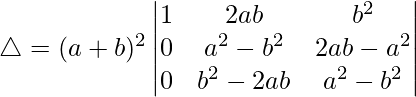
△ = (a + b)2 [1((a2 – b2)(a2 – b2) – (b2 – 2ab)(2ab – a2))]
△ = (a + b)2 [(a2 – b2)2 + (b2 – 2ab)(a2 – 2ab)]
△ = (a + b)2 [(a2 + b2 – ab)2]
△ = (a3 + b3)2
Hence proved
问题 26。 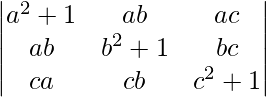 = 1 + a 2 + b 2 + c 2
= 1 + a 2 + b 2 + c 2
解决方案:
Considering the determinant, we have
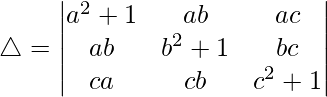
Multiplying a, b and c to R1, R2 and R3 we get

Taking a, b and c common from C1, C2 and C3 we get
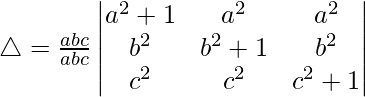
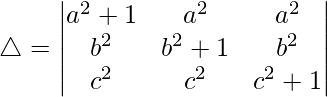
R1⇢R1 + R2 + R3
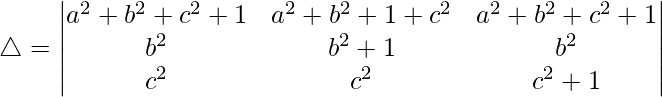
Taking (a2 + b2 + c2 + 1) common from R1, we get

C2⇢C2-C1 and C3⇢C3-C1
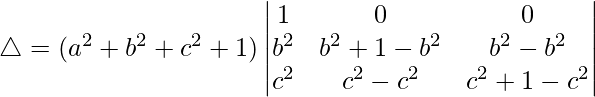
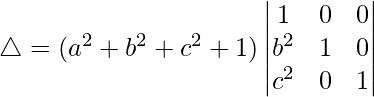
△ = (a2 + b2 + c2 + 1)[1((1)(1) – (0)(0))]
△ = (a2 + b2 + c2 + 1)[1]
△ = (a2 + b2 + c2 + 1)
Hence proved !!
问题 27。 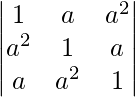 = (a 3 – 1) 2
= (a 3 – 1) 2
解决方案:
Considering the determinant, we have
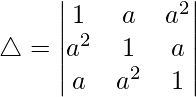
C1⇢C1 + C2 + C3
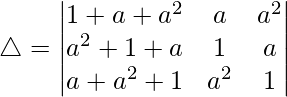
Taking (a2 + a + 1) common from C1, we get
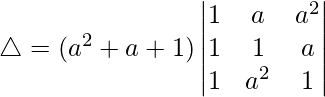
R2⇢R2 – R1 and R3⇢R3 – R1
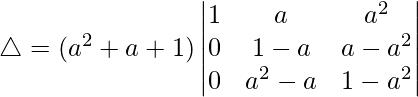
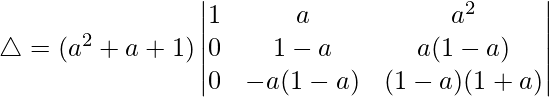
Taking (1 – a) common from R2 and R3, we get

△ = (a2 + a + 1)(1 – a)2[1((1 + a)(1) – (a)(-a))]
△ = (a2 + a + 1)(1 – a)2[(1 + a) + a2]
△ = (a2 + a + 1)(1 – a)2[1 + a + a2]
△ = ((a2 + a + 1)(1 – a))2
△ = (a3 – 1)2
Hence proved
问题 28。 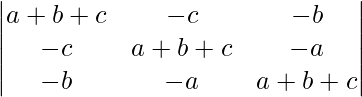 = 2(a + b)(b + c)(c + a)
= 2(a + b)(b + c)(c + a)
解决方案:
Considering the determinant, we have
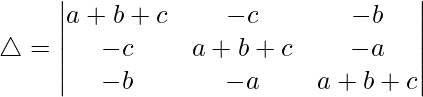
C1⇢C1 + C3 and C2⇢C2 + C3
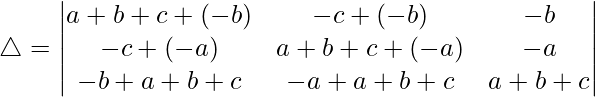
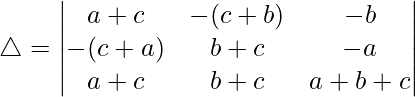
Taking (c + a) and (b + c) common from C1 and C2, we get
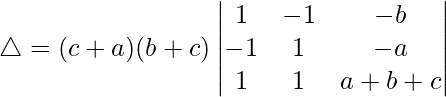
R2⇢R2 + R1 and R3⇢R3 + R2
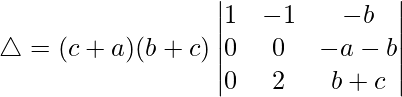
△ = (c + a)(b + c)[1((0)(b + c) – (2)(-a – b))]
△ = (c + a)(b + c)[0 + 2(a + b)]
△ = 2(a + b)(c + a)(b + c)
Hence proved
问题 29。 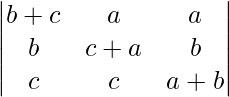 = 4abc
= 4abc
解决方案:
Considering the determinant, we have
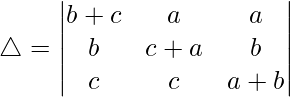
R1⇢R1 + R2 + R3
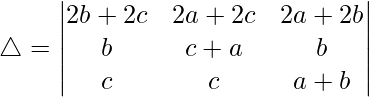
Taking 2 common from R1, we get
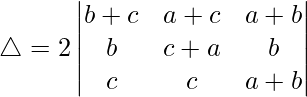
R2⇢R2 – R1 and R3⇢R3 – R1
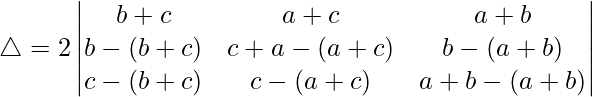
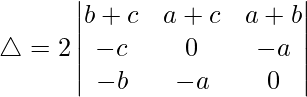
R1⇢R1 + R2 + R3
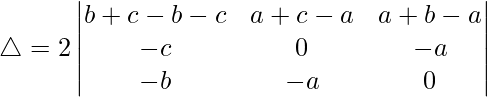
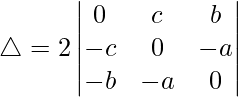
△ = 2[-c((-c)(0) – (-a)(-b)) + b((-c)(-a) – (0)(-b))]
△ = 2[-c(0 – ab) + b(ac – 0)]
△ = 2[abc + abc]
△ = 2[2abc]
△ = 4abc
Hence proved
问题 30。  = 4a 2 b 2 c 2
= 4a 2 b 2 c 2
解决方案:
Considering the determinant, we have
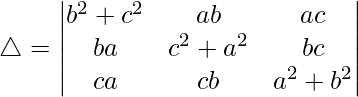
Multiplying a, b and c to R1, R2 and R3 respectively, we get
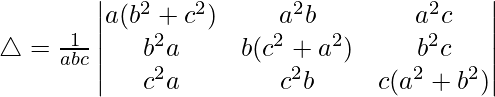
Taking common a, b and c to C1, C2 and C3 respectively, we get
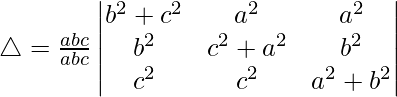

R1⇢R1 + R2 + R3

Taking 2 common from R1, we get
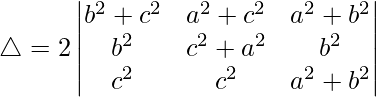
R1⇢R1 – R2
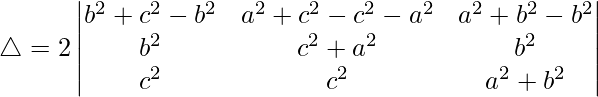
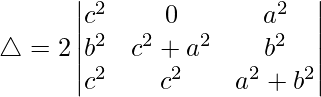
△ = 2
△ = 2
△ = 2
△ = 2
问题 31。 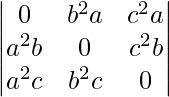 = 2a 3 b 3 c 3
= 2a 3 b 3 c 3
解决方案:
Considering the determinant, we have
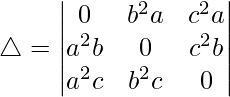
Taking a2, b2 and c2 common from C1, C2 and C3. we get
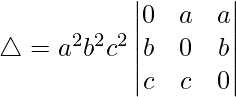
Taking a, b and c common from R1, R2 and R3. we get
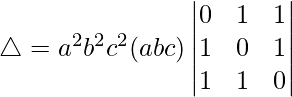
C2⇢C2 – C3
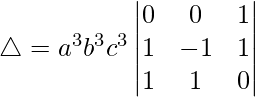
△ = a3b3c3[1((1)(1) – (1)(-1))]
△ = a3b3c3[1 + 1]
△ = 2a3b3c3
Hence proved
问题 32。 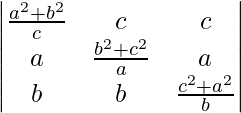 = 4abc
= 4abc
解决方案:
Considering the determinant, we have
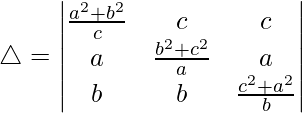
Multiplying c, a and b to R1, R2 and R3. We get
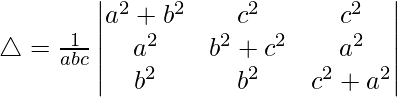
R1⇢R1 – R2 – R3
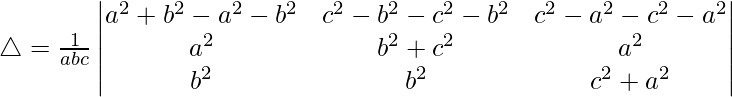
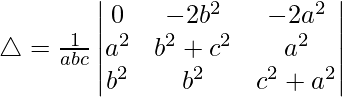
Taking -2 common from R1, we get
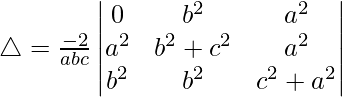
R2⇢R2 – R1 and R3⇢R3 – R1
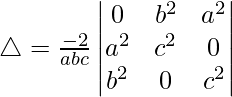
![Rendered by QuickLaTeX.com \triangle = \frac{-2}{abc}[-b^2((a^2)(c^2)-(0)(b^2))+a^2((a^2)(0)-(b^2)(c^2))]\\ \triangle = \frac{-2}{abc}[-b^2(a^2c^2)+a^2(-b^2c^2)]\\ \triangle = \frac{-2}{abc}[-b^2a^2c^2-a^2b^2c^2]\\ \triangle = \frac{-2}{abc}[-2a^2b^2c^2]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_6_Determinants_%E2%80%93_Exercise_6.2_%7C_Set_2_98.jpg)
△ = 4abc
Hence proved
问题 33。 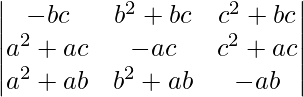 = (ab + bc + ca) 3
= (ab + bc + ca) 3
解决方案:
Considering the determinant, we have
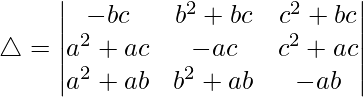
Multiplying a, b and c to R1, R2 and R3. We get
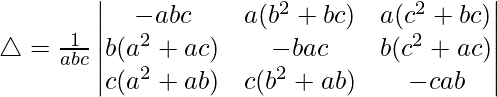
Taking a, b and c common from C1, C2 and C3. we get
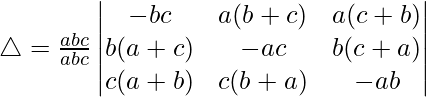
R1⇢R1 + R2 + R3
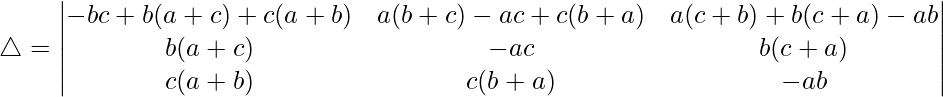
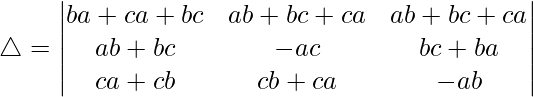
Taking (ab + bc + ca) common from R1, we get
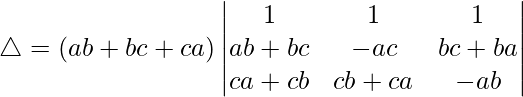
C1⇢C1 – C2 and C3⇢C3 – C2
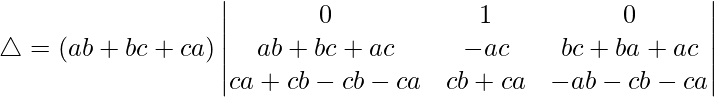
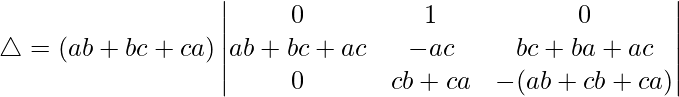
Taking (ab + bc + ca) common from C1 and C2, we get
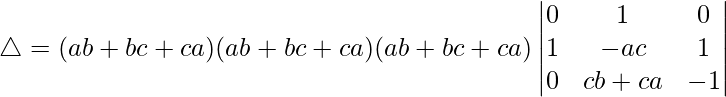
△ = (ab + bc + ca)3 [-1((1)(-1) – (1)(0))]
△ = (ab + bc + ca)3 [-1(-1)]
△ = (ab + bc + ca)3
Hence proved
问题 34。 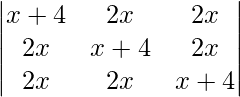 = (5x + 4)(4 -x) 2
= (5x + 4)(4 -x) 2
解决方案:
Considering the determinant, we have
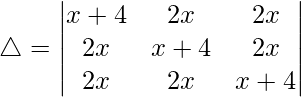
C1⇢C1 + C2 + C3
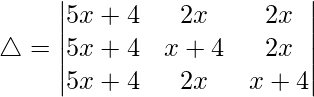
Taking (5x + 4) common from C1, we get
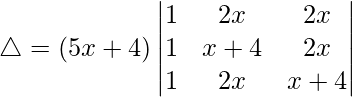
R2⇢R2 – R1 and R3⇢R3 – R1
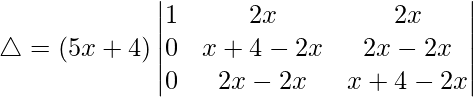
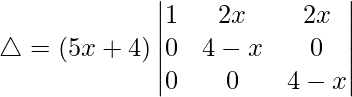
△ = (5x + 4)[1((4 – x)(4 – x) – (0)(0))]
△ = (5x + 4)[(4 – x)2]
△ = (5x + 4)(4 – x)2
Hence proved