问题1.找到以下给出的以下函数的最大值和最小值:
(i)f(x)=(2x – 1) 2 + 3
解决方案:
Given that, f(x) = (2x – 1)2 + 3
From the given function we observe that
(2x – 1)2 ≥ 0 ∀ x∈ R,
So,
(2x – 1)2 + 3 ≥ 3 ∀ x∈ R,
Now we find the minimum value of function f when 2x-1 = 0
So, x = 1/2
f = f(1/2) = (2(1/2) – 1)2 + 3 = 3
Hence, the minimum value of the function is 3 and this function does not contain maximum value.
(ii)f(x)= 9x 2 + 12x + 2
解决方案:
Given that, f(x) = 9x2 + 12x + 2
we can also write as f(x) = (3x + 2)2 – 2
From the given function we observe that
(3x + 2)2 ≥ 0 ∀ x∈ R,
So,
(3x + 2)2 – 2 ≥ 2 ∀ x∈ R,
Now we find the minimum value of function f when 3x + 2 = 0
So, x = -2/3
f = f(-2/3) = (3(-2/3) + 2)2 – 2 = -2
Hence, the minimum value of the function is -2 and this function does not contain maximum value.
(iii)f(x)=-(x – 1) 2 + 10
解决方案:
Given that, f(x) = -(x – 1)2 + 10
From the given function we observe that
(x – 1)2 ≥ 0 ∀ x∈ R,
So,
-(x – 1)2 + 10 ≤ 10 ∀ x∈ R,
Now we find the maximum value of function f when x – 1 = 0
So, x = 1
f = f(1) = -(1 – 1)2 +10 = 10
Hence, the maximum value of the function is 10 and this function does not contain minimum value.
(iv)g(x)= x 3 +1
解决方案:
Given that, g(x) = x3 + 1
When x —> ∞, then g(x) —> ∞
When x —> -∞, then g(x) —> -∞
So, this function has neither minimum nor maximum value
问题2。找到以下给出的以下函数的最大值和最小值:
(i)f(x)= | x + 2 | – 1
解决方案:
Given that, f(x) = |x + 2| – 1
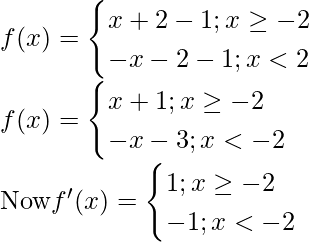
At x = -2 f'(x) change sign from negative to positive, hence by first derivative test, x = -2
is a point of local minima.
So, the minimum value f = f(-1)= |(-1)+ 2| – 1 = -1
So this function doesn’t contain maximum value
(ii)g(x)=-| x + 1 | + 3
解决方案:
Given that, g(x) = -|x + 1| + 3
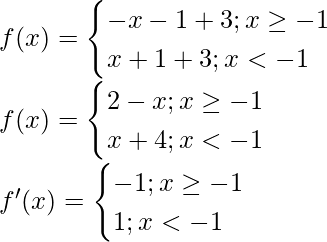
At x = -1 f'(x) change sign from positive to negative, hence by first derivative test, x = -1
is a point of local minima.
So, the maximum value of f = f(-1) = -|(-1) + 1| + 3 = 3
So, this function doesn’t contain minimum value
(iii)h(x)=罪2x + 5
解决方案:
Given that, h(x) = sin(2x) + 5
On differentiate both side w.r.t x, we get
h'(x) = 2cos2x
Now put h'(x) = 0
2cos 2x = 0
2x = (2x – 1)π/2
x = (2x – 1)π/4
![]()
Let’s perform second derivative test,
h”(x) = -4sin2x
h”(π/4) < 0
![]()
& so on.
So, ![]()
of local maxima.
& ![]() are points of local minima.
are points of local minima.
So, the minimum value of the given function is 4 and the maximum value of the given function is 6
(iv)f(x)= | sin(4x + 3)|
解决方案:
Given that, f(x) = |sin(4x + 3)|
Now for any value of x, sin4x has the least value as -1. i.e., sin 4x + 3 ≥ 2
So f(x) = |sin(4x + 3)| = sin 4x + 3
On differentiate both side w.r.t x, we get
f'(x) = 4cos4x
Now put f'(x) = 0
4cos 4x = 0
4x = (2x – 1)π/2
x = (2x – 1)π/8
![]() & son on
& son on
Let’s perform second derivative test,
f”(x) = -16 sin4x
f”(π/8) < 0; f”(3π/8) > 0; f”(5π/8) < 0
So,![]() …. are points of local maxima. Minimum value = 4.
…. are points of local maxima. Minimum value = 4.
& ![]() are points of local minima. Minimum value = 2.
are points of local minima. Minimum value = 2.
(v)h(x)= x + 1,x∈(-1,1)
解决方案:
Given that, h(x) = x + 1, x ∈ (-1, 1)
As we can clearly see from the function that h(x) is a strictly increasing function.
So, the minimum value of x will give minimum value of h(x).
Now, x ∈ (-1, 1)
So, thi function has no minimum nor maximum value.
问题3.找到以下函数的局部最大值和局部最小值(如果有)。还要找到局部最大值和局部最小值(视情况而定):
(i)f(x)= x 2
解决方案:
Given that f(x) = x2
On differentiate both side w.r.t x, we get
f'(x) = 2x
Now put f'(x) = 0
2x = 0
x = 0
Let’s do second derivative test,
f”(x) = 2 > 0
At, x = 0, f'(x) = 0 and f”(x) > 0,
So x = 0 is a point of local minima. Local minimum value.
(ii)g(x)= x 3 – 3x
解决方案:
Given that g(x) = x3 – 3x
On differentiate both side w.r.t x, we get
g'(x) = 3x2 – 3
Now put g'(x) = 0
3x2 – 3 = 0
x2 = 1
x = ±1
Let’s do the second derivative test,
g”(x) = 6x ….(i)
g”(1) = 6 > 0
g”(-1) = -6 > 0
So by second derivatives test, x = 1 is a point of local maxima and the maximum value is
g(1) = (1)3 – 3(1) = -2
So by second derivatives test, x = -1 is a point of local minima and the minimum value is
g(-1) = (-1)3 – 3(-1) = 2
Hence, the local minimum value is -2 and the local maximum value is 2
(iii)h(x)= sin x + cos x,0
解决方案:
h(x) = sin x + cos x, x∈(0,π/2)
On differentiate both side w.r.t x, we get
h'(x) = cos x – sin x
Now put h'(x) = 0
cos x – sin x = 0
cos x = sin x, x ∈ (0, π/2)
Clearly x = π/4 [both cos x and sin x attain 1/√2 at π/4]
Let’s do second derivative test,
h”(x) = -sin x – cos x
h”(π/4) = 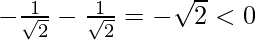
At 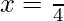 is a point of local maxima and the maximum value is
is a point of local maxima and the maximum value is
h(π/4) = sin π/4 + cos π/4
= 1/√2 + 1/√2 = √2
(iv)f(x)= sin x – cos x,0
解决方案:
Given that, f(x) = sin x – cos x, x ∈ (0, 2π)
On differentiate both side w.r.t x, we get
f'(x) = cos x + sin x
Now put f'(x) = 0
cos x + sin x = 0
x = 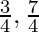 in (0, 2π)
in (0, 2π)
Now let’s do the second derivative test
f”(x) = -sin x + cos x
f”(3π/4) = – √2 > 0
f”(7π/4) = √2 > 0
So by second derivatives test, x = 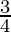 is a point of local maxima and the maximum value is
is a point of local maxima and the maximum value is
f(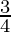 ) = -sin 3π/4 + cos 3π
) = -sin 3π/4 + cos 3π
4 = 1/√2 + 1/√2 = √2 > 0
So by second derivatives test, x = 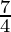 is a point of local minima and the minimum value is
is a point of local minima and the minimum value is
f(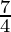 ) = -sin 7π/4 + cos 7π
) = -sin 7π/4 + cos 7π
4 = -1/√2 – 1/√2 = -√2 > 0
Hence, the local minimum value is -√2 and the local maximum value is √2.
(v)f(x)= x 3 – 6x 2 + 9x + 15
解决方案:
Given that, f(x) = x3 – 6x2 + 9x + 15
On differentiate both side w.r.t x, we get
f'(x) = 3x2 – 12x + 9
Now put f'(x) = 0
3x2 – 12x + 9 = 0
3(x2 – 4x + 3) = 0
x = 1, 3
Let’s do the second derivative test,
f”(x) = 6x – 12
f”(1) = -6 < 0
f”(3) = 6 > 0
So by second derivatives test, x = 1 is a point of local maxima and the maximum value is
f'(1) = 3(1)2 – 12(1) + 9 = 19
So by second derivatives test, x = 3 is a point of local minima and the minimum value is
f'(3) = 3(3)2 – 12(3) + 9 = 15
Hence, the local minimum value is 15 and the local maximum value is 19.
(六) 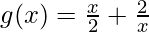 ,x> 0
,x> 0
解决方案:
Given that, 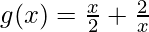 , x > 0
, x > 0
On differentiate both side w.r.t x, we get
g'(x)=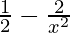
Now put g'(x) = 0
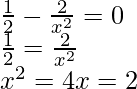 but ‘x > 0’
but ‘x > 0’
So, x = 2
Now we will do the second derivative test,
g”(x)=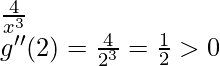
Hence, x = 2 is a point of local minima.
Local maximum value = g(2) = 2
(vii) 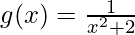
解决方案:
Given that, 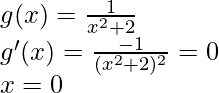
On differentiate both side w.r.t x, we get
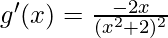
Now put g'(x) = 0

Now, let’s perform the second derivative test,
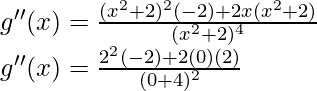
= -8/16 = -1/2 < 0
At x = 0, g'(x) = 0 and g”(x) < 0
Hence, ‘x = 0’ is a point of local maxima.
Now the domain of g(x) is (-∞, ∞).
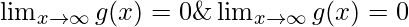
Value of g(x) at the extreme values of x is 0
So the global maxima of g(x)=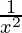 is at x = 0.
is at x = 0.
The maximum value is g(0) = 1/2
(viii) 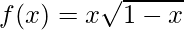 ,x> 0
,x> 0
解决方案:
Given that, 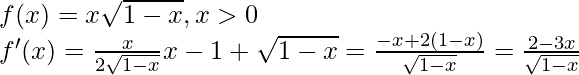
Now put f'(x) = 0
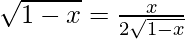
2(1 – x) = x
2 – 2x = x
3x = 2
x = 2/3
Now let’s do the second derivative test,
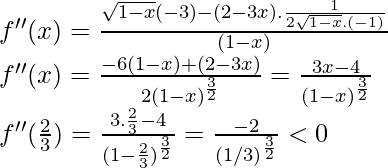
x = 2/3 is a point of local maxima f(2/3) = 
Now, f (x) = x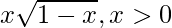
For domain, 1 – x ≥ 0 or x ≤ 1
So x ∈ [0, 1]
Local maxima is at x = 2/3 and the local maximum value is 
问题4.证明以下函数没有最大值或最小值:
(i)f(x)= e x
解决方案:
Given that, f(x) = ex
f'(x) = ex
Now ex > 0, f'(x) > 0
Hence, f(x) is a strictly increasing function with no maxima or minima.
(ii)g(x)=对数x
解决方案:
Given that, g(x) = log x
g'(x) = 1/x
Now the domain of log x is x > 0
So, 1/x > 0, i.e., g'(x) > 0
Hence, g(x) is a strictly increasing function with no maxima or minima.
(iii)h(x)= x 3 + x 2 + x + 1
解决方案:
Given that, h(x) = x3 + x2 + x + 1
h'(x) = 3x2 + 2x + 1
Now for this quadratic expression 3x2 + 2x + 1,
Its discriminant 0 = 22 – 4(3)(1) = -8 < 0
So, 3x2 + 2x + 1 > 0
Hence, h(x) is a strictly increasing function with no maxima or minima.
问题5.在给定的时间间隔中找到以下函数的绝对最大值和绝对最小值:
(i)f(x)= x 3 ,x∈[-2,2]
解决方案:
Given that, f(x) = x3, x ∈ [-2, 2]
f'(x) = 3x2
f'(x) = 0 at x = 0
f”(x) = 6x
f”(0) = 0, second derivative failure
Now f'(3+) > 0 and f'(3–) > 0
f'(x) does not change sign at x = 0.
x = 0 is neither maxima nor minima
f(x) = x3 is a strictly increasing function.
(ii)f(x)= sin x + cos x,x∈[0,π]
解决方案:
Given that, f(x) = sin x + cos x, x ∈ [0, π]
First derivative
f'(x) = cos x – sin x
Now put f'(x) = 0
cos x = sin x
x = π/4
On applying second derivative test,
f”(x) = -sin x – cos x
f”(π/4) = 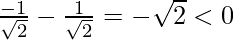
Hence, x = π/4 is pof local maxima . f(π/4)=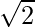
Now, for global maxima = max{f(0), f(π/4), f(π)}
= max{1, √2, -1}
For global maxima is at x = π/4 and the global maximum value is √2.
Now, for global minima = max{f(0), f(π/4), f(π)}
= max{1, √2, -1}
Global minima is at x = π and the global minimum value is -1.
(iii) ![由QuickLaTeX.com渲染 f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions%20%E2%80%93%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%206%20Application%20of%20Derivatives%20%E2%80%93%20Exercise%206.5%20%7C%20Set%201_37.jpg)
解决方案:
Given that, ![Rendered by QuickLaTeX.com f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions%20%E2%80%93%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%206%20Application%20of%20Derivatives%20%E2%80%93%20Exercise%206.5%20%7C%20Set%201_38.jpg)
f'(x) = 4 – x
Now put f'(x) = 0
4 – x = 0
x = 4
Now applying second derivative test f”(x) = -1 < 0
Hence, x = 4 is a pt. of local maxima.
f(4) = 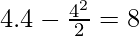
Global maxima = max{f(-2), f(4), f(9/2)}
= max{-10, 8, 7.8}
= 8
Global maxima occur at x = 9/2 and global maximum value is f(9/2) = 8
Global minima = min{f(-2), f(4), f(9/2)}
= max{-10, 8, 16.9}
= -10
Global minima occur at x = -2 and the global minimum value is f(-2) = -10.
(iv)f(x)=(x – 1) 2 + 3,x∈[-3,1]
解决方案:
Given that, f(x) = (x – 1)2 + 3, x ∈ [-3, 1]
f'(x) = 2(x – 1)
Now put f'(x) = 0
2(x – 1) = 0
x = 1
Now applying second order derivative test,
f”(x) = 2 > 0
Hence, x = 1 is a point of local minima. f(1) = 3
Global maxima = max{f(-3), f(1)}
= max{19, 3}
= 19
The global or absolute maxima occurs at x = -3 and the absolute maximum value is f(-3) = 19
Global minima = min{f(-3), f(1)}
= min{19, 3]
= 3
The global or absolute minima occurs at x = 1 and the absolute value is f(1) = 3
问题6.如果利润函数由p(x)= 41 – 24x – 18x 2给出,求出公司可以赚取的最大利润
解决方案:
Given that p(x) = 41 – 24x – 18x2
p'(x) = -24 – 36x
Now put p'(x) = 0
-24 – 36x = 0
x = -24/36
x = -2/3
Now, doing the second order derivative test,
p”(x) = -36 < 0
Hence, x = -2/3 is point of local maxima.
Now in quadratic function with domain R, if there is a local maxima, it is the global maxima also. BC3 p(-∞)⇢ -∞ and p(+∞)⇢ -∞
The maximum profit is p(-2/3) = 49
If negative units (x) do not exist, then maximum profit is p(0) = 41.
问题7.在区间[0,3]上找到最大值和最小值3x 4 – 8x 3 + 12x 2 – 48x + 25。
解决方案:
Given that f(x) = 3x4 – 8x3 + 12x2 – 48x + 25, x ∈ [0, 3]
f'(x) = 12x2 – 24x2 + 24x – 48
Now put f'(x) = 0
12x3 – 24x2 + 24x – 48 = 0
12(x2 – 2x2 + 2x – 4) = 0
12(x2(x – 2) + 2(x – 2)) = 0
12(x2 + 2)(x – 2) = 0
x = 2 because x2 + 2 ≠ 0
Now applying second derivative test,
f”(x) = 12(3x2 – 4x + 2)
f”(2) = 12(3.22 – 4.2 + 2)
f”(2) = 12.6 = 72 > 0
Hence, x = 2 is point of local minima.
f(2) = -39
Global maxima = max{f(0), f(2), f(3)}
= max{25, -39, 16}
= 25
Global maxima occur at x = 0 and the global maximum is 25.
Global minima = min{f(0), f(2), f(3)}
= min{25, -39, 16}
= -39
Global minima occur at x = 2 andthe global minimum value is -39.
问题8.在区间[0,2π]的哪些点,函数sin 2x是否达到最大值?
解决方案:
Given that, f(x) = sin 2x , x ∈ [0, 2π]
f'(x) = 2 cos 2x
Now put f'(x) = 0
2cos2x = 0
2x = (2x – 1)π/2
x = (2x – 1)π/4
x = π/4, 3π/4, 5π/4, 7π/4
Now let’s do second order derivative test.
f”(x) = -4 sin2x
f”(π/4) = 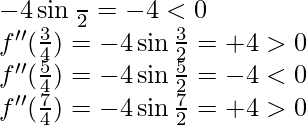
x = π/4 and x = 5π/4 are point of local maxima.
x = 3π/4 and x = 7π/4 are point of local minima.
f(π/4) = f(5π/4) = 1 and f(3π/4) = f(7π/4) = -1
Now,
Global maxima = max{f(0), f(π/4), f(3π/4), f{5π/4}, f(7π/4), f(2π)}
= max{0, 1, -1, 1, -1, 0}
= 1
Global maxima occur at the points x = π/4 and x = 5π/4 and the absolute maximum value is 1.
问题9.函数sin x + cos x的最大值是多少?
解决方案:
Given that, f(x) = sin x + cos x
f'(x) = cos x – sin x
Now put f'(x) = 0
cos x = sin x

= {-√2, √2, +√2, -√2, -√2}
Now, second order derivative test,
f”(x) = -sin x – cos x
f”(π/4) = f”(9π/4) = f”(17π/4)……….. = -√2 < 0
A liter ⇢ f(x) = sin x + cos x = 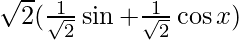
= 
问题10.在间隔[1,3]中找到2x 3 – 24x + 107的最大值。在[-3,-1]中找到相同函数的最大值。
解决方案:
Given that f(x) = 2x3 – 24x + 107
On differentiating w.r.t. x we get
f'(x) = 6x2 – 24
Now, put f'(x) = 0
6x2 = 24
x2 = 4
x = ±2
Now second order test
f”(x) = 12x
f”(2) = 12.2 = 24 > 0
x = 2 is a pt. of local minima
f(2) = 75
f”(-2) = 12(-2) = -24 < 0
x = -2 is point of local maxima. f(-2) = 139
Now, in the interval [1, 3]
Global maxima = max{f(1), f(2), f(3)}
= max{85, 75, 89}
= 89
Now, in the interval [-3,-1]
Global maxima = max{f(-3), f(-2), f(-1)}
= max{125, 139, 129}
= 139
问题11假定在x = 1时,函数x 4 – 62x 2 + ax + 9在间隔[0,2]上达到最大值。查找a的值。
解决方案:
Give that, f(x) = x4 – 62x2 + ax + 9
On differentiating w.r.t. x we get
f'(x) = 4x3 – 124x + a
The maximum value is attained at x = 1, and 1 lies between 0 and 2.
So, at x = 1, there must be a local maxima
That means, f'(1) = 0
f'(1) = 4(1)3 – 124(1) + a = 0
-120 + a = 0
a = 120
问题12.在[0,2π]上找到x + sin2x的最大值和最小值。
解决方案:
Give that f(x) = x + sin2x, x ∈ [0, 2π]
On differentiating w.r.t. x we get
f'(x) = 1 + 2cos2x
Now put f'(x) = 0, we get
1 + 2cos2x = 0
cos2x = -1/2
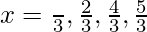 ∈ [0, 2π]
∈ [0, 2π]
Now,
For global maxima = max{f(0), f(π/3), f(4π/3), f(2π)}
= max{0, π/3, 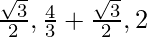 }
}
= 2π
Global maxima occur at x = 2π and the maximum value is f(2π) = 2π.
For global minima = min{f(0), f(2π/3), f(5π/3), f(2π)}
= min{0, 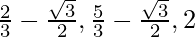 }
}
= 0
Global minima occur at x = 0 and the minimum value is 0.
解决方案:
h(x) = sin x + cos x, x∈(0,π/2)
On differentiate both side w.r.t x, we get
h'(x) = cos x – sin x
Now put h'(x) = 0
cos x – sin x = 0
cos x = sin x, x ∈ (0, π/2)
Clearly x = π/4 [both cos x and sin x attain 1/√2 at π/4]
Let’s do second derivative test,
h”(x) = -sin x – cos x
h”(π/4) = ![]()
At ![]() is a point of local maxima and the maximum value is
is a point of local maxima and the maximum value is
h(π/4) = sin π/4 + cos π/4
= 1/√2 + 1/√2 = √2
(iv)f(x)= sin x – cos x,0
解决方案:
Given that, f(x) = sin x – cos x, x ∈ (0, 2π)
On differentiate both side w.r.t x, we get
f'(x) = cos x + sin x
Now put f'(x) = 0
cos x + sin x = 0
x = 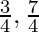 in (0, 2π)
in (0, 2π)
Now let’s do the second derivative test
f”(x) = -sin x + cos x
f”(3π/4) = – √2 > 0
f”(7π/4) = √2 > 0
So by second derivatives test, x = 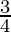 is a point of local maxima and the maximum value is
is a point of local maxima and the maximum value is
f(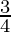 ) = -sin 3π/4 + cos 3π
) = -sin 3π/4 + cos 3π
4 = 1/√2 + 1/√2 = √2 > 0
So by second derivatives test, x = 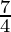 is a point of local minima and the minimum value is
is a point of local minima and the minimum value is
f(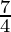 ) = -sin 7π/4 + cos 7π
) = -sin 7π/4 + cos 7π
4 = -1/√2 – 1/√2 = -√2 > 0
Hence, the local minimum value is -√2 and the local maximum value is √2.
(v)f(x)= x 3 – 6x 2 + 9x + 15
解决方案:
Given that, f(x) = x3 – 6x2 + 9x + 15
On differentiate both side w.r.t x, we get
f'(x) = 3x2 – 12x + 9
Now put f'(x) = 0
3x2 – 12x + 9 = 0
3(x2 – 4x + 3) = 0
x = 1, 3
Let’s do the second derivative test,
f”(x) = 6x – 12
f”(1) = -6 < 0
f”(3) = 6 > 0
So by second derivatives test, x = 1 is a point of local maxima and the maximum value is
f'(1) = 3(1)2 – 12(1) + 9 = 19
So by second derivatives test, x = 3 is a point of local minima and the minimum value is
f'(3) = 3(3)2 – 12(3) + 9 = 15
Hence, the local minimum value is 15 and the local maximum value is 19.
(六) 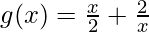 ,x> 0
,x> 0
解决方案:
Given that, 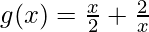 , x > 0
, x > 0
On differentiate both side w.r.t x, we get
g'(x)=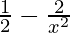
Now put g'(x) = 0
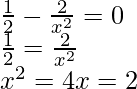 but ‘x > 0’
but ‘x > 0’
So, x = 2
Now we will do the second derivative test,
g”(x)=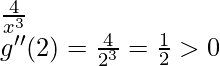
Hence, x = 2 is a point of local minima.
Local maximum value = g(2) = 2
(vii) 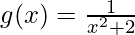
解决方案:
Given that, 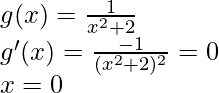
On differentiate both side w.r.t x, we get
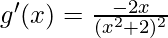
Now put g'(x) = 0

Now, let’s perform the second derivative test,
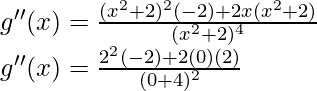
= -8/16 = -1/2 < 0
At x = 0, g'(x) = 0 and g”(x) < 0
Hence, ‘x = 0’ is a point of local maxima.
Now the domain of g(x) is (-∞, ∞).
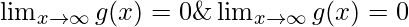
Value of g(x) at the extreme values of x is 0
So the global maxima of g(x)=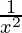 is at x = 0.
is at x = 0.
The maximum value is g(0) = 1/2
(viii) 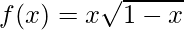 ,x> 0
,x> 0
解决方案:
Given that, 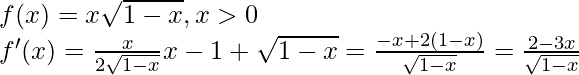
Now put f'(x) = 0
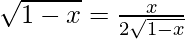
2(1 – x) = x
2 – 2x = x
3x = 2
x = 2/3
Now let’s do the second derivative test,
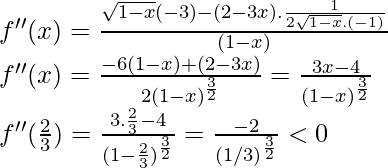
x = 2/3 is a point of local maxima f(2/3) = 
Now, f (x) = x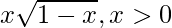
For domain, 1 – x ≥ 0 or x ≤ 1
So x ∈ [0, 1]
Local maxima is at x = 2/3 and the local maximum value is 
问题4.证明以下函数没有最大值或最小值:
(i)f(x)= e x
解决方案:
Given that, f(x) = ex
f'(x) = ex
Now ex > 0, f'(x) > 0
Hence, f(x) is a strictly increasing function with no maxima or minima.
(ii)g(x)=对数x
解决方案:
Given that, g(x) = log x
g'(x) = 1/x
Now the domain of log x is x > 0
So, 1/x > 0, i.e., g'(x) > 0
Hence, g(x) is a strictly increasing function with no maxima or minima.
(iii)h(x)= x 3 + x 2 + x + 1
解决方案:
Given that, h(x) = x3 + x2 + x + 1
h'(x) = 3x2 + 2x + 1
Now for this quadratic expression 3x2 + 2x + 1,
Its discriminant 0 = 22 – 4(3)(1) = -8 < 0
So, 3x2 + 2x + 1 > 0
Hence, h(x) is a strictly increasing function with no maxima or minima.
问题5.在给定的时间间隔中找到以下函数的绝对最大值和绝对最小值:
(i)f(x)= x 3 ,x∈[-2,2]
解决方案:
Given that, f(x) = x3, x ∈ [-2, 2]
f'(x) = 3x2
f'(x) = 0 at x = 0
f”(x) = 6x
f”(0) = 0, second derivative failure
Now f'(3+) > 0 and f'(3–) > 0
f'(x) does not change sign at x = 0.
x = 0 is neither maxima nor minima
f(x) = x3 is a strictly increasing function.
(ii)f(x)= sin x + cos x,x∈[0,π]
解决方案:
Given that, f(x) = sin x + cos x, x ∈ [0, π]
First derivative
f'(x) = cos x – sin x
Now put f'(x) = 0
cos x = sin x
x = π/4
On applying second derivative test,
f”(x) = -sin x – cos x
f”(π/4) = 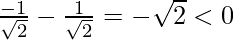
Hence, x = π/4 is pof local maxima . f(π/4)=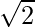
Now, for global maxima = max{f(0), f(π/4), f(π)}
= max{1, √2, -1}
For global maxima is at x = π/4 and the global maximum value is √2.
Now, for global minima = max{f(0), f(π/4), f(π)}
= max{1, √2, -1}
Global minima is at x = π and the global minimum value is -1.
(iii) ![由QuickLaTeX.com渲染 f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions%20%E2%80%93%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%206%20Application%20of%20Derivatives%20%E2%80%93%20Exercise%206.5%20%7C%20Set%201_37.jpg)
解决方案:
Given that, ![Rendered by QuickLaTeX.com f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions%20%E2%80%93%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%206%20Application%20of%20Derivatives%20%E2%80%93%20Exercise%206.5%20%7C%20Set%201_38.jpg)
f'(x) = 4 – x
Now put f'(x) = 0
4 – x = 0
x = 4
Now applying second derivative test f”(x) = -1 < 0
Hence, x = 4 is a pt. of local maxima.
f(4) = 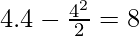
Global maxima = max{f(-2), f(4), f(9/2)}
= max{-10, 8, 7.8}
= 8
Global maxima occur at x = 9/2 and global maximum value is f(9/2) = 8
Global minima = min{f(-2), f(4), f(9/2)}
= max{-10, 8, 16.9}
= -10
Global minima occur at x = -2 and the global minimum value is f(-2) = -10.
(iv)f(x)=(x – 1) 2 + 3,x∈[-3,1]
解决方案:
Given that, f(x) = (x – 1)2 + 3, x ∈ [-3, 1]
f'(x) = 2(x – 1)
Now put f'(x) = 0
2(x – 1) = 0
x = 1
Now applying second order derivative test,
f”(x) = 2 > 0
Hence, x = 1 is a point of local minima. f(1) = 3
Global maxima = max{f(-3), f(1)}
= max{19, 3}
= 19
The global or absolute maxima occurs at x = -3 and the absolute maximum value is f(-3) = 19
Global minima = min{f(-3), f(1)}
= min{19, 3]
= 3
The global or absolute minima occurs at x = 1 and the absolute value is f(1) = 3
问题6.如果利润函数由p(x)= 41 – 24x – 18x 2给出,求出公司可以赚取的最大利润
解决方案:
Given that p(x) = 41 – 24x – 18x2
p'(x) = -24 – 36x
Now put p'(x) = 0
-24 – 36x = 0
x = -24/36
x = -2/3
Now, doing the second order derivative test,
p”(x) = -36 < 0
Hence, x = -2/3 is point of local maxima.
Now in quadratic function with domain R, if there is a local maxima, it is the global maxima also. BC3 p(-∞)⇢ -∞ and p(+∞)⇢ -∞
The maximum profit is p(-2/3) = 49
If negative units (x) do not exist, then maximum profit is p(0) = 41.
问题7.在区间[0,3]上找到最大值和最小值3x 4 – 8x 3 + 12x 2 – 48x + 25。
解决方案:
Given that f(x) = 3x4 – 8x3 + 12x2 – 48x + 25, x ∈ [0, 3]
f'(x) = 12x2 – 24x2 + 24x – 48
Now put f'(x) = 0
12x3 – 24x2 + 24x – 48 = 0
12(x2 – 2x2 + 2x – 4) = 0
12(x2(x – 2) + 2(x – 2)) = 0
12(x2 + 2)(x – 2) = 0
x = 2 because x2 + 2 ≠ 0
Now applying second derivative test,
f”(x) = 12(3x2 – 4x + 2)
f”(2) = 12(3.22 – 4.2 + 2)
f”(2) = 12.6 = 72 > 0
Hence, x = 2 is point of local minima.
f(2) = -39
Global maxima = max{f(0), f(2), f(3)}
= max{25, -39, 16}
= 25
Global maxima occur at x = 0 and the global maximum is 25.
Global minima = min{f(0), f(2), f(3)}
= min{25, -39, 16}
= -39
Global minima occur at x = 2 andthe global minimum value is -39.
问题8.在区间[0,2π]的哪些点,函数sin 2x是否达到最大值?
解决方案:
Given that, f(x) = sin 2x , x ∈ [0, 2π]
f'(x) = 2 cos 2x
Now put f'(x) = 0
2cos2x = 0
2x = (2x – 1)π/2
x = (2x – 1)π/4
x = π/4, 3π/4, 5π/4, 7π/4
Now let’s do second order derivative test.
f”(x) = -4 sin2x
f”(π/4) = 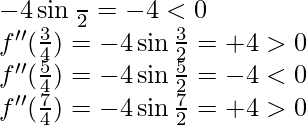
x = π/4 and x = 5π/4 are point of local maxima.
x = 3π/4 and x = 7π/4 are point of local minima.
f(π/4) = f(5π/4) = 1 and f(3π/4) = f(7π/4) = -1
Now,
Global maxima = max{f(0), f(π/4), f(3π/4), f{5π/4}, f(7π/4), f(2π)}
= max{0, 1, -1, 1, -1, 0}
= 1
Global maxima occur at the points x = π/4 and x = 5π/4 and the absolute maximum value is 1.
问题9.函数sin x + cos x的最大值是多少?
解决方案:
Given that, f(x) = sin x + cos x
f'(x) = cos x – sin x
Now put f'(x) = 0
cos x = sin x

= {-√2, √2, +√2, -√2, -√2}
Now, second order derivative test,
f”(x) = -sin x – cos x
f”(π/4) = f”(9π/4) = f”(17π/4)……….. = -√2 < 0
A liter ⇢ f(x) = sin x + cos x = 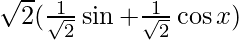
= 
问题10.在间隔[1,3]中找到2x 3 – 24x + 107的最大值。在[-3,-1]中找到相同函数的最大值。
解决方案:
Given that f(x) = 2x3 – 24x + 107
On differentiating w.r.t. x we get
f'(x) = 6x2 – 24
Now, put f'(x) = 0
6x2 = 24
x2 = 4
x = ±2
Now second order test
f”(x) = 12x
f”(2) = 12.2 = 24 > 0
x = 2 is a pt. of local minima
f(2) = 75
f”(-2) = 12(-2) = -24 < 0
x = -2 is point of local maxima. f(-2) = 139
Now, in the interval [1, 3]
Global maxima = max{f(1), f(2), f(3)}
= max{85, 75, 89}
= 89
Now, in the interval [-3,-1]
Global maxima = max{f(-3), f(-2), f(-1)}
= max{125, 139, 129}
= 139
问题11假定在x = 1时,函数x 4 – 62x 2 + ax + 9在间隔[0,2]上达到最大值。查找a的值。
解决方案:
Give that, f(x) = x4 – 62x2 + ax + 9
On differentiating w.r.t. x we get
f'(x) = 4x3 – 124x + a
The maximum value is attained at x = 1, and 1 lies between 0 and 2.
So, at x = 1, there must be a local maxima
That means, f'(1) = 0
f'(1) = 4(1)3 – 124(1) + a = 0
-120 + a = 0
a = 120
问题12.在[0,2π]上找到x + sin2x的最大值和最小值。
解决方案:
Give that f(x) = x + sin2x, x ∈ [0, 2π]
On differentiating w.r.t. x we get
f'(x) = 1 + 2cos2x
Now put f'(x) = 0, we get
1 + 2cos2x = 0
cos2x = -1/2
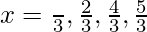 ∈ [0, 2π]
∈ [0, 2π]
Now,
For global maxima = max{f(0), f(π/3), f(4π/3), f(2π)}
= max{0, π/3, 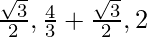 }
}
= 2π
Global maxima occur at x = 2π and the maximum value is f(2π) = 2π.
For global minima = min{f(0), f(2π/3), f(5π/3), f(2π)}
= min{0, 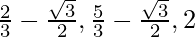 }
}
= 0
Global minima occur at x = 0 and the minimum value is 0.
解决方案:
Given that, f(x) = sin x – cos x, x ∈ (0, 2π)
On differentiate both side w.r.t x, we get
f'(x) = cos x + sin x
Now put f'(x) = 0
cos x + sin x = 0
x = ![]() in (0, 2π)
in (0, 2π)
Now let’s do the second derivative test
f”(x) = -sin x + cos x
f”(3π/4) = – √2 > 0
f”(7π/4) = √2 > 0
So by second derivatives test, x = ![]() is a point of local maxima and the maximum value is
is a point of local maxima and the maximum value is
f(![]() ) = -sin 3π/4 + cos 3π
) = -sin 3π/4 + cos 3π
4 = 1/√2 + 1/√2 = √2 > 0
So by second derivatives test, x = ![]() is a point of local minima and the minimum value is
is a point of local minima and the minimum value is
f(![]() ) = -sin 7π/4 + cos 7π
) = -sin 7π/4 + cos 7π
4 = -1/√2 – 1/√2 = -√2 > 0
Hence, the local minimum value is -√2 and the local maximum value is √2.
(v)f(x)= x 3 – 6x 2 + 9x + 15
解决方案:
Given that, f(x) = x3 – 6x2 + 9x + 15
On differentiate both side w.r.t x, we get
f'(x) = 3x2 – 12x + 9
Now put f'(x) = 0
3x2 – 12x + 9 = 0
3(x2 – 4x + 3) = 0
x = 1, 3
Let’s do the second derivative test,
f”(x) = 6x – 12
f”(1) = -6 < 0
f”(3) = 6 > 0
So by second derivatives test, x = 1 is a point of local maxima and the maximum value is
f'(1) = 3(1)2 – 12(1) + 9 = 19
So by second derivatives test, x = 3 is a point of local minima and the minimum value is
f'(3) = 3(3)2 – 12(3) + 9 = 15
Hence, the local minimum value is 15 and the local maximum value is 19.
(六) 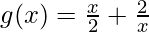 ,x> 0
,x> 0
解决方案:
Given that, ![]() , x > 0
, x > 0
On differentiate both side w.r.t x, we get
g'(x)=![]()
Now put g'(x) = 0
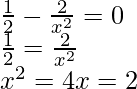 but ‘x > 0’
but ‘x > 0’
So, x = 2
Now we will do the second derivative test,
g”(x)=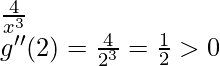
Hence, x = 2 is a point of local minima.
Local maximum value = g(2) = 2
(vii) 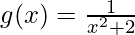
解决方案:
Given that, 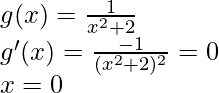
On differentiate both side w.r.t x, we get
![]()
Now put g'(x) = 0
![]()
Now, let’s perform the second derivative test,
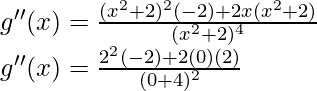
= -8/16 = -1/2 < 0
At x = 0, g'(x) = 0 and g”(x) < 0
Hence, ‘x = 0’ is a point of local maxima.
Now the domain of g(x) is (-∞, ∞).
![]()
Value of g(x) at the extreme values of x is 0
So the global maxima of g(x)=![]() is at x = 0.
is at x = 0.
The maximum value is g(0) = 1/2
(viii) 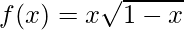 ,x> 0
,x> 0
解决方案:
Given that, 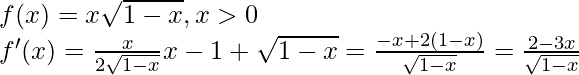
Now put f'(x) = 0
![]()
2(1 – x) = x
2 – 2x = x
3x = 2
x = 2/3
Now let’s do the second derivative test,
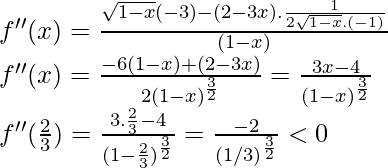
x = 2/3 is a point of local maxima f(2/3) = ![]()
Now, f (x) = x![]()
For domain, 1 – x ≥ 0 or x ≤ 1
So x ∈ [0, 1]
Local maxima is at x = 2/3 and the local maximum value is ![]()
问题4.证明以下函数没有最大值或最小值:
(i)f(x)= e x
解决方案:
Given that, f(x) = ex
f'(x) = ex
Now ex > 0, f'(x) > 0
Hence, f(x) is a strictly increasing function with no maxima or minima.
(ii)g(x)=对数x
解决方案:
Given that, g(x) = log x
g'(x) = 1/x
Now the domain of log x is x > 0
So, 1/x > 0, i.e., g'(x) > 0
Hence, g(x) is a strictly increasing function with no maxima or minima.
(iii)h(x)= x 3 + x 2 + x + 1
解决方案:
Given that, h(x) = x3 + x2 + x + 1
h'(x) = 3x2 + 2x + 1
Now for this quadratic expression 3x2 + 2x + 1,
Its discriminant 0 = 22 – 4(3)(1) = -8 < 0
So, 3x2 + 2x + 1 > 0
Hence, h(x) is a strictly increasing function with no maxima or minima.
问题5.在给定的时间间隔中找到以下函数的绝对最大值和绝对最小值:
(i)f(x)= x 3 ,x∈[-2,2]
解决方案:
Given that, f(x) = x3, x ∈ [-2, 2]
f'(x) = 3x2
f'(x) = 0 at x = 0
f”(x) = 6x
f”(0) = 0, second derivative failure
Now f'(3+) > 0 and f'(3–) > 0
f'(x) does not change sign at x = 0.
x = 0 is neither maxima nor minima
f(x) = x3 is a strictly increasing function.
(ii)f(x)= sin x + cos x,x∈[0,π]
解决方案:
Given that, f(x) = sin x + cos x, x ∈ [0, π]
First derivative
f'(x) = cos x – sin x
Now put f'(x) = 0
cos x = sin x
x = π/4
On applying second derivative test,
f”(x) = -sin x – cos x
f”(π/4) = ![]()
Hence, x = π/4 is pof local maxima . f(π/4)=![]()
Now, for global maxima = max{f(0), f(π/4), f(π)}
= max{1, √2, -1}
For global maxima is at x = π/4 and the global maximum value is √2.
Now, for global minima = max{f(0), f(π/4), f(π)}
= max{1, √2, -1}
Global minima is at x = π and the global minimum value is -1.
(iii) ![由QuickLaTeX.com渲染 f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20NCERT%20Solutions%20%E2%80%93%20Mathematics%20Part%20I%20%E2%80%93%20Chapter%206%20Application%20of%20Derivatives%20%E2%80%93%20Exercise%206.5%20%7C%20Set%201_37.jpg)
解决方案:
Given that, ![]()
f'(x) = 4 – x
Now put f'(x) = 0
4 – x = 0
x = 4
Now applying second derivative test f”(x) = -1 < 0
Hence, x = 4 is a pt. of local maxima.
f(4) = ![]()
Global maxima = max{f(-2), f(4), f(9/2)}
= max{-10, 8, 7.8}
= 8
Global maxima occur at x = 9/2 and global maximum value is f(9/2) = 8
Global minima = min{f(-2), f(4), f(9/2)}
= max{-10, 8, 16.9}
= -10
Global minima occur at x = -2 and the global minimum value is f(-2) = -10.
(iv)f(x)=(x – 1) 2 + 3,x∈[-3,1]
解决方案:
Given that, f(x) = (x – 1)2 + 3, x ∈ [-3, 1]
f'(x) = 2(x – 1)
Now put f'(x) = 0
2(x – 1) = 0
x = 1
Now applying second order derivative test,
f”(x) = 2 > 0
Hence, x = 1 is a point of local minima. f(1) = 3
Global maxima = max{f(-3), f(1)}
= max{19, 3}
= 19
The global or absolute maxima occurs at x = -3 and the absolute maximum value is f(-3) = 19
Global minima = min{f(-3), f(1)}
= min{19, 3]
= 3
The global or absolute minima occurs at x = 1 and the absolute value is f(1) = 3
问题6.如果利润函数由p(x)= 41 – 24x – 18x 2给出,求出公司可以赚取的最大利润
解决方案:
Given that p(x) = 41 – 24x – 18x2
p'(x) = -24 – 36x
Now put p'(x) = 0
-24 – 36x = 0
x = -24/36
x = -2/3
Now, doing the second order derivative test,
p”(x) = -36 < 0
Hence, x = -2/3 is point of local maxima.
Now in quadratic function with domain R, if there is a local maxima, it is the global maxima also. BC3 p(-∞)⇢ -∞ and p(+∞)⇢ -∞
The maximum profit is p(-2/3) = 49
If negative units (x) do not exist, then maximum profit is p(0) = 41.
问题7.在区间[0,3]上找到最大值和最小值3x 4 – 8x 3 + 12x 2 – 48x + 25。
解决方案:
Given that f(x) = 3x4 – 8x3 + 12x2 – 48x + 25, x ∈ [0, 3]
f'(x) = 12x2 – 24x2 + 24x – 48
Now put f'(x) = 0
12x3 – 24x2 + 24x – 48 = 0
12(x2 – 2x2 + 2x – 4) = 0
12(x2(x – 2) + 2(x – 2)) = 0
12(x2 + 2)(x – 2) = 0
x = 2 because x2 + 2 ≠ 0
Now applying second derivative test,
f”(x) = 12(3x2 – 4x + 2)
f”(2) = 12(3.22 – 4.2 + 2)
f”(2) = 12.6 = 72 > 0
Hence, x = 2 is point of local minima.
f(2) = -39
Global maxima = max{f(0), f(2), f(3)}
= max{25, -39, 16}
= 25
Global maxima occur at x = 0 and the global maximum is 25.
Global minima = min{f(0), f(2), f(3)}
= min{25, -39, 16}
= -39
Global minima occur at x = 2 andthe global minimum value is -39.
问题8.在区间[0,2π]的哪些点,函数sin 2x是否达到最大值?
解决方案:
Given that, f(x) = sin 2x , x ∈ [0, 2π]
f'(x) = 2 cos 2x
Now put f'(x) = 0
2cos2x = 0
2x = (2x – 1)π/2
x = (2x – 1)π/4
x = π/4, 3π/4, 5π/4, 7π/4
Now let’s do second order derivative test.
f”(x) = -4 sin2x
f”(π/4) = 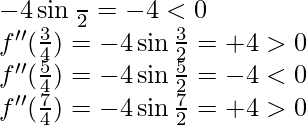
x = π/4 and x = 5π/4 are point of local maxima.
x = 3π/4 and x = 7π/4 are point of local minima.
f(π/4) = f(5π/4) = 1 and f(3π/4) = f(7π/4) = -1
Now,
Global maxima = max{f(0), f(π/4), f(3π/4), f{5π/4}, f(7π/4), f(2π)}
= max{0, 1, -1, 1, -1, 0}
= 1
Global maxima occur at the points x = π/4 and x = 5π/4 and the absolute maximum value is 1.
问题9.函数sin x + cos x的最大值是多少?
解决方案:
Given that, f(x) = sin x + cos x
f'(x) = cos x – sin x
Now put f'(x) = 0
cos x = sin x
![]()
= {-√2, √2, +√2, -√2, -√2}
Now, second order derivative test,
f”(x) = -sin x – cos x
f”(π/4) = f”(9π/4) = f”(17π/4)……….. = -√2 < 0
A liter ⇢ f(x) = sin x + cos x = ![]()
= ![]()
问题10.在间隔[1,3]中找到2x 3 – 24x + 107的最大值。在[-3,-1]中找到相同函数的最大值。
解决方案:
Given that f(x) = 2x3 – 24x + 107
On differentiating w.r.t. x we get
f'(x) = 6x2 – 24
Now, put f'(x) = 0
6x2 = 24
x2 = 4
x = ±2
Now second order test
f”(x) = 12x
f”(2) = 12.2 = 24 > 0
x = 2 is a pt. of local minima
f(2) = 75
f”(-2) = 12(-2) = -24 < 0
x = -2 is point of local maxima. f(-2) = 139
Now, in the interval [1, 3]
Global maxima = max{f(1), f(2), f(3)}
= max{85, 75, 89}
= 89
Now, in the interval [-3,-1]
Global maxima = max{f(-3), f(-2), f(-1)}
= max{125, 139, 129}
= 139
问题11假定在x = 1时,函数x 4 – 62x 2 + ax + 9在间隔[0,2]上达到最大值。查找a的值。
解决方案:
Give that, f(x) = x4 – 62x2 + ax + 9
On differentiating w.r.t. x we get
f'(x) = 4x3 – 124x + a
The maximum value is attained at x = 1, and 1 lies between 0 and 2.
So, at x = 1, there must be a local maxima
That means, f'(1) = 0
f'(1) = 4(1)3 – 124(1) + a = 0
-120 + a = 0
a = 120
问题12.在[0,2π]上找到x + sin2x的最大值和最小值。
解决方案:
Give that f(x) = x + sin2x, x ∈ [0, 2π]
On differentiating w.r.t. x we get
f'(x) = 1 + 2cos2x
Now put f'(x) = 0, we get
1 + 2cos2x = 0
cos2x = -1/2
![]() ∈ [0, 2π]
∈ [0, 2π]
Now,
For global maxima = max{f(0), f(π/3), f(4π/3), f(2π)}
= max{0, π/3, ![]() }
}
= 2π
Global maxima occur at x = 2π and the maximum value is f(2π) = 2π.
For global minima = min{f(0), f(2π/3), f(5π/3), f(2π)}
= min{0, ![]() }
}
= 0
Global minima occur at x = 0 and the minimum value is 0.