第 12 类 RD Sharma 解决方案 – 第 11 章微分 – 练习 11.5 |设置 3

问题 41. 如果 (sin x) ^y = (cos y) ^x ，证明$\frac{dy}{dx}=\frac{log cosy-ycotx}{logsinx+xtany}$ .

解决方案：

We have, 

=> (sin x)^y = (cos y)^x

On taking log of both the sides, we get,

=> log (sin x)^y = log (cos y)^x

=> y log (sin x) = x log (cos y)

On differentiating both sides with respect to x, we get,

=> $y[(\frac{1}{sinx})(cosx)]+log(sin x)(\frac{dy}{dx})=x[(\frac{1}{cosy})(-siny)(\frac{dy}{dx})]+log (cos y)$

=> $ycotx+log(sin x)(\frac{dy}{dx})=-xtany(\frac{dy}{dx})+log (cos y)$

=> $[log(sin x)+xtany](\frac{dy}{dx})=log (cos y)-ycotx$

=> $\frac{dy}{dx}=\frac{log cosy-ycotx}{logsinx+xtany}$

Hence proved.

问题 42. 如果 (cos x) ^y = (tan y) ^x ，证明 \frac{dy}{dx}=\frac{log tany+ytanx}{logcosx-xsecycosecy} 。

解决方案：

We have, (cos x)^y = (tan y)^x

On taking log of both the sides, we get,

=> log (cos x)^y = log (tan y)^x

=> y log (cos x) = x log (tan y)

On differentiating both sides with respect to x, we get,

=> $y[(\frac{1}{cosx})(-sinx)]+log (cos x)(\frac{dy}{dx})=x[(\frac{1}{tany})(sec^2y)(\frac{dy}{dx})]+log (tan y)$

=> $-ytanx+log(cos x)(\frac{dy}{dx})=(\frac{xsec^2y}{tany})(\frac{dy}{dx})+log (tan y)$

=> $-ytanx-log (tan y)=(\frac{xsec^2y}{tany})(\frac{dy}{dx})-log(cos x)(\frac{dy}{dx})$

=> $ytanx+log (tan y)=log(cos x)(\frac{dy}{dx})-(\frac{xsec^2y}{tany})(\frac{dy}{dx})$

=> $ytanx+log (tan y)=log(cos x)(\frac{dy}{dx})-(\frac{x}{cos^2y}×\frac{cosy}{siny})(\frac{dy}{dx})$

=> $ytanx+log (tan y)=log(cos x)(\frac{dy}{dx})-(\frac{x}{cosy}×\frac{1}{siny})(\frac{dy}{dx})$

=> $ytanx+log (tan y)=log(cos x)(\frac{dy}{dx})-(xsecycosecy)(\frac{dy}{dx})$

=> $ytanx+log (tan y)=[log(cos x)-(xsecycosecy)]\frac{dy}{dx}$

=> $[log(cos x)-(xsecycosecy)]\frac{dy}{dx}=ytanx+log (tan y)$

=> $\frac{dy}{dx}=\frac{ytanx+log (tan y)}{log(cos x)-xsecycosecy}$

Hence proved.

问题 43. 如果 e ^x + e ^y = e ^x+y ，证明$\frac{dy}{dx}+e^{y-x}=0$ .

解决方案：

We have,

=> e^x + e^y = e^x+y

On differentiating both sides with respect to x, we get,

=> $e^x+e^y(\frac{dy}{dx})=e^{x+y}(1+\frac{dy}{dx})$

=> $e^x+e^y(\frac{dy}{dx})=e^{x+y}+e^{x+y}(\frac{dy}{dx})$

=> $e^y(\frac{dy}{dx})-e^{x+y}(\frac{dy}{dx})=e^{x+y}-e^x$

=> $\frac{dy}{dx}(e^y-e^{x+y})=e^{x+y}-e^x$

=> $\frac{dy}{dx}=\frac{e^{x+y}-e^x}{e^y-e^{x+y}}$

=> $\frac{dy}{dx}=\frac{e^x+e^y-e^x}{e^y-e^x-e^y}$

=> $\frac{dy}{dx}=-e^{y-x}$

=> $\frac{dy}{dx}+e^{y-x}=0$

Hence proved.

问题 44. 如果 e ^y = y ^x ，证明$\frac{dy}{dx}=\frac{(logy)^2}{logy-1}$ .

解决方案：

We have,

=> e^y = y^x

On taking log of both the sides, we get,

=> log e^y = log y^x

=> y log e = x log y

=> y = x log y

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=x(\frac{1}{y})(\frac{dy}{dx})+logy$

=> $\frac{dy}{dx}=(\frac{x}{y})(\frac{dy}{dx})+logy$

=> $\frac{dy}{dx}-(\frac{x}{y})(\frac{dy}{dx})=logy$

=> $\frac{dy}{dx}(1-\frac{x}{y})=logy$

=> $\frac{dy}{dx}(\frac{y-x}{y})=logy$

=> $\frac{dy}{dx}=\frac{ylogy}{y-x}$

=> $\frac{dy}{dx}=\frac{ylogy}{y-\frac{y}{logy}}$

=> $\frac{dy}{dx}=\frac{ylogy}{\frac{ylogy-y}{logy}}$

=> $\frac{dy}{dx}=\frac{y(logy)^2}{ylogy-y}$

=> $\frac{dy}{dx}=\frac{y(logy)^2}{y(logy-1)}$

Hence proved.

问题 45. 如果 e ^x+y - x = 0，证明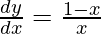$\frac{dy}{dx}=\frac{1-x}{x}$ .

解决方案：

We have,

=> e^x+y − x = 0

On differentiating both sides with respect to x, we get,

=> $e^{x+y}(1+\frac{dy}{dx}) − 1 = 0$

=> $e^{x+y}(1+\frac{dy}{dx})= 1$

Now, we know e^x+y − x = 0

=> e^x+y = x 

So, we get,

=> $e^{x+y}(1+\frac{dy}{dx})= 1$

=> $x(1+\frac{dy}{dx})= 1$

=> $1+\frac{dy}{dx}=\frac{1}{x}$

=> $\frac{dy}{dx}=\frac{1}{x}-1$

=> $\frac{dy}{dx}=\frac{1-x}{x}$

Hence proved.

问题 46. 如果 y = x sin (a+y)，证明$\frac{dy}{dx}=\frac{sin^2(a+y)}{sin(a+y)-ycos(a+y)}$ .

解决方案：

We have,

=> y = x sin (a+y)

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=x[cos(a+y)(\frac{dy}{dx})]+sin(a+y))(1)$

=> $\frac{dy}{dx}=xcos(a+y)(\frac{dy}{dx})+sin(a+y))$

=> $\frac{dy}{dx}-xcos(a+y)(\frac{dy}{dx})=sin(a+y))$

=> $\frac{dy}{dx}(1-xcos(a+y))=sin(a+y))$

Now we know, y = x sin (a+y)

=> $x=\frac{y}{sin(a+y)}$

So, we get,

=> $\frac{dy}{dx}(1-\frac{y}{sin(a+y)}cos(a+y))=sin(a+y))$

=> $\frac{dy}{dx}(1-\frac{ycos(a+y)}{sin(a+y)})=sin(a+y))$

=> $\frac{dy}{dx}(\frac{sin(a+y)-ycos(a+y)}{sin(a+y)})=sin(a+y))$

=> $\frac{dy}{dx}=\frac{sin^2(a+y)}{sin(a+y)-ycos(a+y)}$

Hence proved.

问题 47. 如果 x sin (a+y) + sin a cos (a+y) = 0，证明$\frac{dy}{dx}=\frac{sin^2(a+y)}{sina}$ .

解决方案：

We have,

=> x sin (a+y) + sin a cos (a+y) = 0

On differentiating both sides with respect to x, we get,

=> $x(cos (a+y))(\frac{dy}{dx})+sin(a+y)(1)+sina [-sin(a+y)(\frac{dy}{dx})] = 0$

=> $x(cos (a+y))(\frac{dy}{dx})+sin(a+y)-sinasin(a+y)(\frac{dy}{dx}) = 0$

=> $\frac{dy}{dx}(xcos(a+y)-sinasin(a+y))+sin(a+y)= 0$

=> $\frac{dy}{dx}= \frac{-sin(a+y)}{xcos(a+y)-sinasin(a+y)}$

Now we know, x sin (a+y) + sin a cos (a+y) = 0

=> $x=\frac{-sinacos(a+y)}{sin(a+y)}$

So, we get,

=> $\frac{dy}{dx}= \frac{-sin(a+y)}{(\frac{-sinacos(a+y)}{sin(a+y)})cos(a+y)-sinasin(a+y)}$

=> $\frac{dy}{dx}= \frac{-sin(a+y)}{(\frac{-sinacos^2(a+y)}{sin(a+y)})-sinasin(a+y)}$

=> $\frac{dy}{dx}= \frac{-sin(a+y)}{(\frac{-sinacos^2(a+y)-sinasin^2(a+y)}{sin(a+y)})}$

=> $\frac{dy}{dx}= \frac{-sin(a+y)}{\frac{-sina(cos^2(a+y)+sin^2(a+y))}{sin(a+y)}}$

=> $\frac{dy}{dx}= \frac{-sin(a+y)}{\frac{-sina(1)}{sin(a+y)}}$

=> $\frac{dy}{dx}= \frac{sin(a+y)}{\frac{sina}{sin(a+y)}}$

=> $\frac{dy}{dx}= \frac{sin^2(a+y)}{sina}$

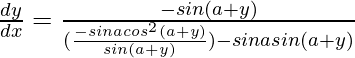
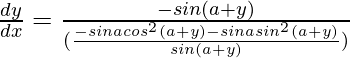
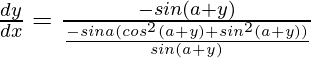
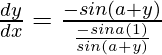
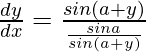
Hence proved.

问题 48. 如果 (sin x) ^y = x + y，证明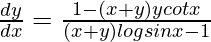$\frac{dy}{dx}=\frac{1-(x+y)ycotx}{(x+y)logsinx-1}$ .

解决方案：

We have,

=> (sin x)^y = x + y

On taking log of both the sides, we get,

=> log (sin x)^y = log (x + y)

=> y log sin x = log (x + y)

On differentiating both sides with respect to x, we get,

=> $y(\frac{1}{sinx})(cosx)+log sin x(\frac{dy}{dx})=\frac{1}{x + y}(1+\frac{dy}{dx})$

=> $ycotx+log sin x(\frac{dy}{dx})=\frac{1}{x + y}+\frac{1}{x+y}\frac{dy}{dx}$

=> $logsinx(\frac{dy}{dx})-\frac{1}{x+y}\frac{dy}{dx}=\frac{1}{x + y}-ycotx$

=> $\frac{dy}{dx}(logsinx-\frac{1}{x+y})=\frac{1}{x + y}-ycotx$

=> $\frac{dy}{dx}(\frac{(x+y)logsinx-1}{x+y})=\frac{1-y(x+y)cotx}{x + y}$

=> $\frac{dy}{dx}[(x+y)logsinx-1]=[1-y(x+y)cotx]$

=> $\frac{dy}{dx}=\frac{1-y(x+y)cotx}{(x+y)logsinx-1}$

Hence proved.

问题 49. 如果 xy log (x+y) = 1，证明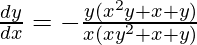$\frac{dy}{dx}=-\frac{y(x^2y+x+y)}{x(xy^2+x+y)}$ .

解决方案：

We have,

=> xy log (x+y) = 1

On differentiating both sides with respect to x, we get,

=> $xy(\frac{1}{x+y})(1+\frac{dy}{dx})+log (x+y)(x\frac{dy}{dx}+y) = 0$

=> $\frac{xy}{x+y}(1+\frac{dy}{dx})+xlog(x+y)\frac{dy}{dx}+ylog(x+y)=0$

=> $\frac{xy}{x+y}+\frac{xy}{x+y}\frac{dy}{dx}+xlog(x+y)\frac{dy}{dx}+ylog(x+y)=0$

Now, we know, xy log (x+y) = 1.

=> $log (x+y) = \frac{1}{xy}$

So, we get,

=> $\frac{xy}{x+y}+\frac{xy}{x+y}\frac{dy}{dx}+xlog(x+y)\frac{dy}{dx}+ylog(x+y)=0$

=> $\frac{xy}{x+y}+\frac{xy}{x+y}\frac{dy}{dx}+x(\frac{1}{xy})\frac{dy}{dx}+y(\frac{1}{xy})=0$

=> $\frac{xy}{x+y}+\frac{xy}{x+y}\frac{dy}{dx}+\frac{1}{y}\frac{dy}{dx}+\frac{1}{x}=0$

=> $\frac{dy}{dx}(\frac{xy}{x+y}+\frac{1}{y})+\frac{xy}{x+y}+\frac{1}{x}=0$

=> $\frac{dy}{dx}(\frac{xy^2+x+y}{y(x+y)})+\frac{x^2y+x+y}{x(x+y)}=0$

=> $\frac{dy}{dx}(\frac{xy^2+x+y}{y(x+y)})=-\frac{x^2y+x+y}{x(x+y)}$

=> $\frac{dy}{dx}(\frac{xy^2+x+y}{y})=-\frac{x^2y+x+y}{x}$

=> $\frac{dy}{dx}=-\frac{y(x^2y+x+y)}{x(xy^2+x+y)}$

Hence proved.

问题 50. 如果 y = x sin y，证明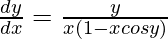$\frac{dy}{dx}=\frac{y}{x(1-xcosy)}$ .

解决方案：

We have,

=> y = x sin y

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=x(cosy)(\frac{dy}{dx})+sin y(1)$

=> $\frac{dy}{dx}=xcosy\frac{dy}{dx}+sin y$

=> $\frac{dy}{dx}(1-xcosy)=sin y$

=> $\frac{dy}{dx}=\frac{sin y}{1-xcosy}$

Now, we know y = x sin y

=> $siny = \frac{y}{x}$

So, we get,

=> $\frac{dy}{dx}=\frac{sin y}{1-xcosy}$

=> $\frac{dy}{dx}=\frac{\frac{y}{x}}{1-xcosy}$

=> $\frac{dy}{dx}=\frac{y}{x(1-xcosy)}$

Hence proved.

问题 51. 求由下式给出的函数f(x) 的导数，

f(x) = (1+x) (1+x ² ) (1+x ⁴ ) (1+x ⁸ )，因此找到 f'(1)。

解决方案：

Here we are given,

=> f(x) = (1+x) (1+x²) (1+x⁴) (1+x⁸)

On differentiating both sides with respect to x, we get,

=> $f'(x)=(1+x)(1+x^2)\frac{d}{dx}(1+x^8)+(1+x)(1+x^2)(1+x^8)\frac{d}{dx}(1+x^4)+(1+x)(1+x^4)(1+x^8)\frac{d}{dx}(1+x^2)+(1+x^2)(1+x^4)(1+x^8)\frac{d}{dx}(1+x)$

=> $f'(x)=(1+x)(1+x^2)(1+x^4)(8x^7)+(1+x)(1+x^2)(1+x^8)(4x^3)+(1+x)(1+x^4)(1+x^8)(2x)+(1+x^2)(1+x^4)(1+x^8)(1)$

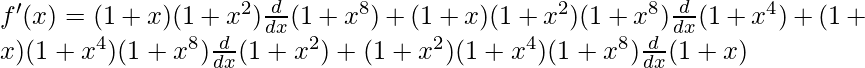
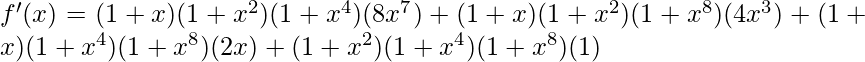
Now, the value of f'(x) at 1 is,

=> f'(1) = (1 + 1) (1 + 1) (1 + 1) (8) + (1 + 1) (1 + 1) (1 + 1) (4) + (1 + 1) (1 + 1) (1 + 1) (2) + (1 + 1) (1 + 1) (1 + 1) (1)

=> f'(1) = (2) (2) (2) (8) + (2) (2) (2) (4) + (2) (2) (2) (2) + (2) (2) (2) (1)

=> f'(1) = 64 + 32 + 16 + 8

=> f'(1) = 120

Therefore, the value of f'(1) is 120.

问题 52. 如果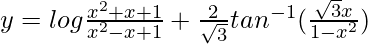$y=log\frac{x^2+x+1}{x^2-x+1}+\frac{2}{\sqrt{3}}tan^{-1}(\frac{\sqrt{3}x}{1-x^2})$ ， 找$\frac{dy}{dx}$ .

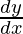解决方案：

We are given,

=> $y=log\frac{x^2+x+1}{x^2-x+1}+\frac{2}{\sqrt{3}}tan^{-1}(\frac{\sqrt{3}x}{1-x^2})$

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=\frac{1}{\frac{x^2+x+1}{x^2-x+1}}\frac{d}{dx}(\frac{x^2+x+1}{x^2-x+1})+\frac{2}{\sqrt{3}}\left[\frac{1}{1+(\frac{\sqrt{3}x}{1-x^2})^2}\right]\frac{d}{dx}(\frac{\sqrt{3}x}{1-x^2})$

=> $\frac{dy}{dx}=\frac{x^2-x+1}{x^2+x+1}\left[\frac{(x^2-x+1)(2x+1)-(x^2+x+1)(2x-1)}{(x^2-x+1)^2}\right]+\frac{2}{\sqrt{3}}\left[\frac{1}{1+\frac{3x^2}{(1-x^2)^2}}\right]\left[\frac{(1-x^2)(\sqrt{3})-\sqrt{3}x(-2x)}{(1-x^2)^2}\right]$

=> $\frac{dy}{dx}=\frac{1}{x^2+x+1}\left[\frac{2x^3+x^2-2x^2-x+2x+1-2x^3-2x^2-2x+x^2+x+1}{x^2-x+1}\right]+\frac{2}{\sqrt{3}}\left[\frac{1}{\frac{(1-x^2)^2+3x^2}{(1-x^2)^2}}\right]\left[\frac{\sqrt{3}-\sqrt{3}x^2+2\sqrt{3}x^2}{(1-x^2)^2}\right]$

=> $\frac{dy}{dx}=\frac{-2x^2+2}{x^4+2x^2+1-x^2}+\frac{2}{\sqrt{3}}\left[\frac{1}{\frac{1+x^4-2x^2+3x^2}{(1-x^2)^2}}\right]\left[\frac{\sqrt{3}+\sqrt{3}x^2}{(1-x^2)^2}\right]$

=> $\frac{dy}{dx}=\frac{-2x^2+2}{x^4+x^2+1}+\frac{2}{\sqrt{3}}\left[\frac{(1-x^2)^2}{1+x^4-2x^2+3x^2}\right]\left[\frac{\sqrt{3}(1+x^2)}{(1-x^2)^2}\right]$

=> $\frac{dy}{dx}=\frac{-2x^2+2}{x^4+x^2+1}+\frac{2}{\sqrt{3}}\left[\frac{\sqrt{3}(1+x^2)}{1+x^4+x^2}\right]$

=> $\frac{dy}{dx}=\frac{-2x^2+2}{x^4+x^2+1}+\frac{2(1+x^2)}{x^4+x^2+1}$

=> $\frac{dy}{dx}=\frac{-2x^2+2+2(1+x^2)}{x^4+x^2+1}$

=> $\frac{dy}{dx}=\frac{-2x^2+2+2+2x^2}{x^4+x^2+1}$

=> $\frac{dy}{dx}=\frac{4}{x^4+x^2+1}$

问题 53. 如果 y = (sin x − cos x) ^{sin x−cos x} , π/4 < x < 3π/4，求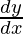$\frac{dy}{dx}$ .

解决方案：

We have,

=> y = (sin x − cos x)^{sin x−cos x}

On taking log of both the sides, we get,

=> log y = log (sin x − cos x)^{sin x−cos x}

=> log y = (sin x − cos x) log (sin x−cos x)

On differentiating both sides with respect to x, we get,

=> $\frac{1}{y}\frac{dy}{dx}=(sinx−cosx)(\frac{1}{sinx-cosx})(cosx+sinx)+log (sin x−cos x)(cosx+sinx)$

=> $\frac{1}{y}\frac{dy}{dx}$= (1)(cosx + sinx) + (cosx + sinx)log (sin x − cos x)

=> $\frac{1}{y}\frac{dy}{dx}$= cosx + sinx + (cosx + sinx)log (sin x − cos x)

=> $\frac{1}{y}\frac{dy}{dx}$= (cosx + sinx)(1 + log (sin x − cos x))

=> $\frac{dy}{dx}$= y(cosx + sinx)(1 + log (sin x − cos x))

=> $\frac{dy}{dx}$= (sinx – cosx)^sinx-cosx(cosx + sinx)(1 + log (sin x − cos x))

问题 54. 求函数xy = e ^xy的 dy/dx。

解决方案：

We have,

=> xy = e^x-y

On taking log of both the sides, we get,

=> log xy = log e^x-y

=> log x + log y = (x − y) log e

=> log x + log y = x − y

On differentiating both sides with respect to x, we get,

=> $\frac{1}{x}+\frac{1}{y}\frac{dy}{dx}= 1 −\frac{dy}{dx}$

=> $\frac{1}{y}\frac{dy}{dx}+\frac{dy}{dx}= 1-\frac{1}{x}$

=> $(\frac{1}{y}+1)\frac{dy}{dx}= 1-\frac{1}{x}$

=> $(\frac{1+y}{y})\frac{dy}{dx}=\frac{x-1}{x}$

=> $\frac{dy}{dx}=\frac{y(x-1)}{x(y+1)}$

问题 55. 求函数y ^x + x ^y + x ^x = a ^b的 dy/dx。

解决方案：

We have,

=> y^x + x^y + x^x = a^b

=> $e^{logy^x}+e^{logx^y}+e^{logx^x} = a^b$

=> $e^{xlogy}+e^{ylogx}+e^{xlogx} = a^b$

On differentiating both sides with respect to x, we get,

=> $(e^{xlogy})[x(\frac{1}{y})(\frac{dy}{dx})+logy]+(e^{ylogx})[y(\frac{1}{x})+logx(\frac{dy}{dx})]+(e^{xlogx})[x(\frac{1}{x})+logx] = 0$

=> $(e^{xlogy})[\frac{x}{y}\frac{dy}{dx}+logy]+(e^{ylogx})[\frac{y}{x}+logx(\frac{dy}{dx})]+(e^{xlogx})[1+logx] = 0$

=> $(y^x)[\frac{x}{y}\frac{dy}{dx}+logy]+(y^x)[\frac{y}{x}+logx(\frac{dy}{dx})]+(x^x)[1+logx] = 0$

=> $(xy^{x-1}+x^ylogy)\frac{dy}{dx}=-x^x(1+logx)-yx^{y-1}-y^xlogy$

=> $(xy^{x-1}+x^ylogy)\frac{dy}{dx}=-[x^x(1+logx)+yx^{y-1}+y^xlogy]$

=> $\frac{dy}{dx}=-\frac{x^x(1+logx)+yx^{y-1}+y^xlogy}{xy^{x-1}+x^ylogy}$

问题 56. 如果 (cos x) ^y = (cos y) ^x ，求 dy/dx。

解决方案：

We have,

=> (cos x)^y = (cos y)^x

On taking log of both the sides, we get,

=> log (cos x)^y = log (cos y)^x

=> y log (cos x) = x log (cos y)

On differentiating both sides with respect to x, we get,

=> $y[(\frac{1}{cosx})(-sinx)]+log (cos x)(\frac{dy}{dx})=x[(\frac{1}{cosy})(-siny)(\frac{dy}{dx})]+log(cos y)$

=> $-ytanx+log (cos x)(\frac{dy}{dx})=-xtany(\frac{dy}{dx})+log(cos y)$

=> $log (cos x)(\frac{dy}{dx})+xtany(\frac{dy}{dx})=log(cos y)+ytanx$

=> $[log (cos x)+xtany]\frac{dy}{dx}=log(cos y)+ytanx$

=> $\frac{dy}{dx}=\frac{log(cos y)+ytanx}{log (cos x)+xtany}$

问题 57. 如果 cos y = x cos (a+y)，其中 cos a ≠ ±1，证明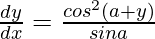$\frac{dy}{dx}=\frac{cos^2(a+y)}{sina}$ .

解决方案：

We have,

=> cos y = x cos (a+y)

On differentiating both sides with respect to x, we get,

=> $(-siny)(\frac{dy}{dx})=x[-sin (a+y)(\frac{dy}{dx})]+cos(a+y)(1)$

=> $-siny(\frac{dy}{dx})=-xsin (a+y)(\frac{dy}{dx})+cos(a+y)$

=> $-siny\frac{dy}{dx}+xsin(a+y)\frac{dy}{dx}=cos(a+y)$

=> $[xsin(a+y)-siny]\frac{dy}{dx}=cos(a+y)$

=> $\frac{dy}{dx}=\frac{cos(a+y)}{xsin(a+y)-siny}$

=> $\frac{dy}{dx}=\frac{cos^2(a+y)}{cos(a+y)[xsin(a+y)-siny]}$

=> $\frac{dy}{dx}=\frac{cos^2(a+y)}{xcos(a+y)sin(a+y)-cos(a+y)siny}$

=> $\frac{dy}{dx}=\frac{cos^2(a+y)}{cosysin(a+y)-cos(a+y)siny}$

=> $\frac{dy}{dx}=\frac{cos^2(a+y)}{sin(a+y-y)}$

=> $\frac{dy}{dx}=\frac{cos^2(a+y)}{sina}$

Hence proved.

问题 58. 如果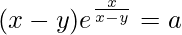$(x-y)e^{\frac{x}{x-y}}=a$ ， 证明$y\frac{dy}{dx}+x=2y$ .

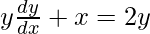解决方案：

We have,

=> $(x-y)e^{\frac{x}{x-y}}=a$

On differentiating both sides with respect to x, we get,

=> $(x-y)\left[(e^{\frac{x}{x-y}})[\frac{(x-y)-x(1-\frac{dy}{dx})}{(x-y)^2}]\right]+e^{\frac{x}{x-y}}(1-\frac{dy}{dx})=0$

=> $\frac{(x-y)-x(1-\frac{dy}{dx})}{(x-y)}+(1-\frac{dy}{dx})=0$

=> $(1-\frac{dy}{dx})(1-\frac{x}{x-y})+1=0$

=> $(1-\frac{dy}{dx})(\frac{x-y-x}{x-y})+1=0$

=> $(1-\frac{dy}{dx})(\frac{-y}{x-y})+1=0$

=> $-y+y\frac{dy}{dx}+x-y=0$

=> $y\frac{dy}{dx}+x=2y$

Hence proved.

问题 59. 如果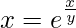$x=e^{\frac{x}{y}}$ ， 证明$\frac{dy}{dx}=\frac{x-y}{xlogx}$ .

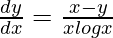解决方案：

We have,

=> $x=e^{\frac{x}{y}}$

On taking log of both the sides, we get,

=> log x = log $e^{\frac{x}{y}}$

=> $logx=\frac{x}{y}loge$

=> $logx=\frac{x}{y}$

=> $y=\frac{x}{logx}$

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=\frac{logx(1)-x(\frac{1}{x})}{(logx)^2}$

=> $\frac{dy}{dx}=\frac{logx-1}{(logx)^2}$

We know, $y=\frac{x}{logx}$

=> $logx=\frac{x}{y}$

So, we get,

=> $\frac{dy}{dx}=\frac{\frac{x}{y}-1}{(logx)^2}$

=> $\frac{dy}{dx}=\frac{\frac{x-y}{y}}{(logx)^2}$

=> $\frac{dy}{dx}=\frac{x-y}{y(logx)^2}$

=> $\frac{dy}{dx}=\frac{x-y}{(\frac{x}{logx})(logx)^2}$

=> $\frac{dy}{dx}=\frac{x-y}{xlogx}$

Hence proved.

问题 60. 如果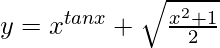$y=x^{tanx}+\sqrt{\frac{x^2+1}{2}}$ , 找到 dy/dx。

解决方案：

We have,

=> $y=x^{tanx}+\sqrt{\frac{x^2+1}{2}}$

=> $y=e^{logx^{tanx}}+e^{log\sqrt{\frac{x^2+1}{2}}}$

=> $y=e^{tanxlogx}+e^{\frac{1}{2}log(\frac{x^2+1}{2})}$

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=(e^{tanxlogx})[tanx(\frac{1}{x})+logx(sec^2x)]+(e^{\frac{1}{2}log(\frac{x^2+1}{2})})(\frac{1}{2})(\frac{2}{x^2+1})(\frac{1}{2})(2x)$

=> $\frac{dy}{dx}=(e^{tanxlogx})[\frac{tanx}{x}+sec^2xlogx]+(e^{\frac{1}{2}log(\frac{x^2+1}{2})})(\frac{x}{x^2+1})$

=> $\frac{dy}{dx}=x^{tanx}[\frac{tanx}{x}+sec^2xlogx]+\sqrt{\frac{x^2+1}{2}}(\frac{x}{x^2+1})$

=> $\frac{dy}{dx}=x^{tanx}[\frac{tanx}{x}+sec^2xlogx]+\frac{x}{\sqrt{2(x^2+1)}}$

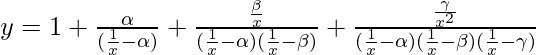问题 61. 如果$y=1+\frac{\alpha}{(\frac{1}{x}-\alpha)}+\frac{\frac{\beta}{x}}{(\frac{1}{x}-\alpha)(\frac{1}{x}-\beta)}+\frac{\frac{\gamma}{x^2}}{(\frac{1}{x}-\alpha)(\frac{1}{x}-\beta)(\frac{1}{x}-\gamma)}$ , 找到 dy/dx。

解决方案：

We are given, 

=> $y=1+\frac{\alpha}{(\frac{1}{x}-\alpha)}+\frac{\frac{\beta}{x}}{(\frac{1}{x}-\alpha)(\frac{1}{x}-\beta)}+\frac{\frac{\gamma}{x^2}}{(\frac{1}{x}-\alpha)(\frac{1}{x}-\beta)(\frac{1}{x}-\gamma)}$

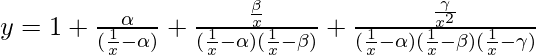
Now we know, 

If $y=1+\frac{ax^2}{(x-a)(x-b)(x-c)}+\frac{bx}{(x-b)(x-c)}+\frac{c}{(x-c)}$ then, $\frac{dy}{dx}=\frac{y}{x}[\frac{a}{a-x}+\frac{b}{b-x}+\frac{c}{c-x}]$

In the given expression, we have 1/x instead of x.

So, using the above theorem, we get,

=> $\frac{dy}{dx}=\frac{\alpha}{(\frac{1}{x}-\alpha)}+\frac{\beta}{(\frac{1}{x}-\beta)}+\frac{\gamma}{(\frac{1}{x}-\gamma)}$