第 12 类 RD Sharma 解决方案 – 第 11 章微分 – 练习 11.5 |设置 2

问题 21. 求 dy/dx 时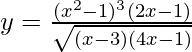$y=\frac{(x^2-1)^3(2x-1)}{\sqrt{(x-3)(4x-1)}}$ .

解决方案：

We have,

=> $y=\frac{(x^2-1)^3(2x-1)}{\sqrt{(x-3)(4x-1)}}$

=> $y=\frac{(x^2-1)^3(2x-1)}{(x-3)^{\frac{1}{2}}(4x-1)^{\frac{1}{2}}}$

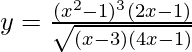
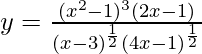
On taking log of both the sides, we get,

=> $log y = log \frac{(x^2-1)^3(2x-1)}{(x-3)^{\frac{1}{2}}(4x-1)^{\frac{1}{2}}}$

=> $log y = log(x^2-1)^{3}+log(2x-1)-log(x-3)^{\frac{1}{2}}-log(4x-1)^{\frac{1}{2}}$

=> $log y = 3log(x^2-1)+log(2x-1)-\frac{1}{2}log(x-3)-\frac{1}{2}log(4x-1)$

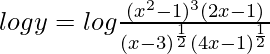
On differentiating both sides with respect to x, we get,

=> $\frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[3log(x^2-1)+log(2x-1)-\frac{1}{2}log(x-3)-\frac{1}{2}log(4x-1)]$

=> $\frac{1}{y}\frac{dy}{dx}=3(\frac{1}{x^2-1})(2x)+2(\frac{1}{2x-1})-\frac{1}{2}(\frac{1}{x-3})-\frac{1}{2}(\frac{1}{4x-1})(4)$

=> $\frac{1}{y}\frac{dy}{dx}=\frac{6x}{x^2-1}+\frac{2}{2x-1}-\frac{1}{2(x-3)}-\frac{2}{4x-1}$

=> $\frac{dy}{dx}=y\left[\frac{6x}{x^2-1}+\frac{2}{2x-1}-\frac{1}{2(x-3)}-\frac{2}{4x-1}\right]$

=> $\frac{dy}{dx}=\frac{(x^2-1)^3(2x-1)}{\sqrt{(x-3)(4x-1)}}\left[\frac{6x}{x^2-1}+\frac{2}{2x-1}-\frac{1}{2(x-3)}-\frac{2}{4x-1}\right]$

问题 22. 找到dy /dx 时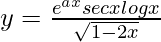$y=\frac{e^{ax}secxlogx}{\sqrt{1-2x}}$ .

解决方案：

We have,

=> $y=\frac{e^{ax}secxlogx}{\sqrt{1-2x}}$

=> $y=\frac{e^{ax}secxlogx}{(1-2x)^{\frac{1}{2}}}$

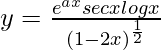
On taking log of both the sides, we get,

=> $log y = log \frac{e^{ax}secxlogx}{(1-2x)^{\frac{1}{2}}}$

=> $log y = loge^{ax}+logsecx+log(logx)-\frac{1}{2}log(1-2x)$

=> $log y = ax+logsecx+log(logx)-\frac{1}{2}log(1-2x)$

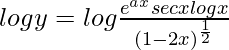
On differentiating both sides with respect to x, we get,

=> $\frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[ax+logsecx+log(logx)-\frac{1}{2}log(1-2x)]$

=> $\frac{1}{y}\frac{dy}{dx}=a+\frac{1}{secx}(secxtanx)+(\frac{1}{logx})(\frac{1}{x})-(\frac{1}{2})(\frac{1}{1-2x})(-2)$

=> $\frac{1}{y}\frac{dy}{dx}=a+tanx+\frac{1}{xlogx}+\frac{1}{1-2x}$

=> $\frac{dy}{dx}=y\left[a+tanx+\frac{1}{xlogx}+\frac{1}{1-2x}\right]$

=> $\frac{dy}{dx}=\frac{e^{ax}secxlogx}{\sqrt{1-2x}}\left[a+tanx+\frac{1}{xlogx}+\frac{1}{1-2x}\right]$

问题 23. 当 y = e ^3x sin 4x 2 ^x时求 dy/dx。

解决方案：

We have 

=> y = e^3x sin 4x 2^x.

On taking log of both the sides, we get,

=> log y = log (e^3x sin 4x 2^x)

=> log y = log e^3x + log (sin 4x) + log 2^x

=> log y = 3x log e + log (sin 4x) + x log 2

=> log y = 3x + log (sin 4x) + x log 2

On differentiating both sides with respect to x, we get,

=> $\frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[3x + log (sin 4x) + x log 2]$

=> $\frac{1}{y}\frac{dy}{dx}=3+(\frac{1}{sin 4x})(4cos4x) + log2$

=> $\frac{1}{y}\frac{dy}{dx}=3+4cotx+log2$

=> $\frac{dy}{dx}=y(3+4cotx+log2)$

=> $\frac{dy}{dx}=2^xe^{3x}sin4x(3+4cotx+log2)$

问题 24. 当 y = sin x sin 2x sin 3x sin 4x 时求 dy/dx。

解决方案：

We have, 

=> y = sin x sin 2x sin 3x sin 4x

On taking log of both the sides, we get,

=> log y = log (sin x sin 2x sin 3x sin 4x)

=> log y = log sin x + log sin 2x + log sin 3x + log sin 4x

On differentiating both sides with respect to x, we get,

=> $\frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}(log sin x + log sin 2x + log sin 3x + log sin 4x)$

=> $\frac{1}{y}\frac{dy}{dx}=\frac{1}{sinx}(cosx)+\frac{1}{sin2x}(2cos2x)+\frac{1}{sin3x}(3cos3x)+\frac{1}{sin4x}(4cos4x)$

=> $\frac{1}{y}\frac{dy}{dx}$= cotx + 2cot2x + 3cot3x + 4cot4x

=> $\frac{dy}{dx}$= y(cotx + 2cot2x + 3cot3x + 4cot4x)

=> $\frac{dy}{dx}$= (sinxsin2x sin3xsin4x)(cotx + 2cot2x + 3cot3x + 4cot4x)

问题 25. 当 y = x ^{sin x} + (sin x) ^x时求 dy/dx。

解决方案：

We have, 

=> y = x^{sin x} + (sin x)^x. 

Let u = x^{sin x} and v = (sin x)^x. Therefore, y = u + v.

Now, u = x^{sin x}

On taking log of both the sides, we get,

=> log u = log x^{sin x}

=> log u = sin x log x

On differentiating both sides with respect to x, we get,

=> $\frac{1}{u}\frac{du}{dx}=\frac{d}{dx}(sin x log x)$

=> $\frac{1}{u}\frac{du}{dx}=sin x(\frac{1}{x})+logxcosx$

=> $\frac{1}{u}\frac{du}{dx}=\frac{sinx}{x}+logxcosx$

=> $\frac{du}{dx}=u\left[\frac{sinx}{x}+logxcosx\right]$

=> $\frac{du}{dx}=x^{sinx}\left[\frac{sinx}{x}+logxcosx\right]$

Also, v = (sin x)^x

On taking log of both the sides, we get,

=> log v = log (sin x)^x

=> log v = x log sin x

On differentiating both sides with respect to x, we get,

=> $\frac{1}{v}\frac{dv}{dx}=\frac{d}{dx}(x log sin x)$

=> $\frac{1}{v}\frac{dv}{dx}=x(\frac{1}{sinx})(cosx)+log(sinx)$

=> $\frac{1}{v}\frac{dv}{dx}=xcotx+log(sinx)$

=> $\frac{dv}{dx}=v[xcotx+log(sinx)]$

=> $\frac{dv}{dx}=(sinx)^x[xcotx+log(sinx)]$

Now we have, y = u + v.

=> $\frac{dy}{dx}=\frac{du}{dx}+\frac{dv}{dx}$

=> $\frac{dy}{dx}=x^{sinx}\left[\frac{sinx}{x}+logxcosx\right]+(sinx)^x[xcotx+log(sinx)]$

问题 26. 当 y = (sin x) ^{cos x} + (cos x) ^{sin x}时求 dy/dx。

解决方案：

We have, 

=> y = (sin x)^{cos x} + (cos x)^{sin x}

=> $y=e^{log(sin x)^{cos x}} + e^{log(cos x)^{sin x}}$

=> $y=e^{cosxlog(sin x)} + e^{sinxlog(cos x)}$

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=\frac{d}{dx}(e^{cosxlog(sin x)} + e^{sinxlog(cos x)})$

=> $\frac{dy}{dx}=(e^{cosxlog(sin x)})[cosx(\frac{1}{sinx})cosx+log(sinx)(-sinx)] + (e^{sinxlog(cos x)})[sinx(\frac{1}{cosx})(-sinx)+log(cosx)(cosx)]$

=> $\frac{dy}{dx}$ = (sinx)^cosx[cosxcotx – sinxlog(sinx)] + (cosx)^sinx[-tanxsinx + cosxlog(cosx)]

=> $\frac{dy}{dx}$ = (sinx)^cosx[cosxcotx – sinxlog(sinx)] + (cosx)^sinx[cosxlog(cosx) – tanxsinx]

问题 27. 当 y = (tan x) ^{cot x} + (cot x) ^{tan x}时求 dy/dx。

解决方案：

We have, 

=> y = (tan x)^{cot x} + (cot x)^{tan x}

=> $y=e^{log(tanx)^{cot x}} + e^{log(cot x)^{tan x}}$

=> $y=e^{cotxlog(tanx)} + e^{tanxlog(cot x)}$

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=\frac{d}{dx}(e^{cotxlog(tanx)} + e^{tanxlog(cot x)})$

=> $\frac{dy}{dx}=(e^{cotxlog(tanx)})[cotx(\frac{1}{tanx})(sec^2x)+log(tanx)(-cosec^2x)] + (e^{tanxlog(cot x)})[tanx(\frac{1}{cotx})(-cosec^2x)+log(cotx)(sec^2x)]$

=> $\frac{dy}{dx}=(tanx)^{cotx}[cot^2x(sec^2x)-log(tanx)(cosec^2x)] + (cotx)^{tanx}[tan^2x(-cosec^2x)+log(cotx)(sec^2x)]$

=> $\frac{dy}{dx}$ = (tanx)^cotx[cosec²x – log(tanx)(cosec²x)] + (cotx)^tanx[-sec²x + log(cotx)(sec²x)]

=> $\frac{dy}{dx}$ = (tanx)^cotx[cosec²x – cosec²xlog(tanx)] + (cotx)^tanx[sec²xlog(cotx) – sec²x]

问题 28. 当 y = (sin x) ^x + sin ⁻¹ √x 时求 dy/dx。

解决方案：

We have, 

=> y = (sin x)^x + sin⁻¹ √x

=> $y=e^{log(sinx)^{x}} + sin^{-1}\sqrt{x}$

=> $y=e^{xlog(sinx)} + sin^{-1}\sqrt{x}$

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=\frac{d}{dx}[e^{xlog(sinx)} + sin^{-1}\sqrt{x}]$

=> $\frac{dy}{dx}=(e^{xlog(sinx)})[x(\frac{1}{sinx})cosx+log(sinx)]+(\frac{1}{\sqrt{1-x}})(\frac{1}{2\sqrt{x}})$

=> $\frac{dy}{dx}=(e^{xlog(sinx)})[xcotx+log(sinx)]+\frac{1}{2\sqrt{x-x^2}}$

=> $\frac{dy}{dx}=(sinx)^x[xcotx+log(sinx)]+\frac{1}{2\sqrt{x-x^2}}$

问题 29. 求 dy/dx 时

(i) y = x ^{cos x} + (sin x) ^{tan x}

解决方案：

We have, 

=> y = x^{cos x} + (sin x)^{tan x}

=> $y=e^{log(x)^{cosx}} + e^{log(sinx)^{tanx}}$

=> $y=e^{cosxlog(x)} + e^{tanxlog(sinx)}$

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=\frac{d}{dx}[e^{cosxlog(x)} + e^{tanxlog(sinx)}]$

=> $\frac{dy}{dx}=(e^{cosxlogx})[cosx(\frac{1}{x})+logx(-sinx)] + (e^{tanxlog(sinx)})[tanx(\frac{1}{sinx})(cosx)+log(sinx)sec^2x]$

=> $\frac{dy}{dx}=x^{cosx}[\frac{cosx}{x}-logxsinx] +(sinx)^{tanx}[tanx(cotx)+log(sinx)sec^2x]$

=> $\frac{dy}{dx}=x^{cosx}[\frac{cosx}{x}-logxsinx] +(sinx)^{tanx}[1+sec^2xlog(sinx)]$

(ii) y = x ^x + (sin x) ^x

解决方案：

We have, 

=> y = x^x + (sin x)^x

=> $y=e^{logx^{x}} + e^{log(sinx)^{x}}$

=> $y=e^{xlogx} + e^{xlog(sinx)}$

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=\frac{d}{dx}[e^{xlogx} + e^{xlog(sinx)}]$

=> $\frac{dy}{dx}=(e^{xlogx})[x(\frac{1}{x})+logx] + (e^{xlog(sinx)})[x(\frac{1}{sinx})(cosx)+log(sinx)]$

=> $\frac{dy}{dx}=(e^{xlogx})[1+logx] + (e^{xlog(sinx)})[xcotx+log(sinx)]$

=> $\frac{dy}{dx}=x^x(1+logx) + (sinx)^x[xcotx+log(sinx)]$

问题 30. 当 y = (tan x) ^{log x} + cos ² (π/4) 时，求 dy/dx。

解决方案：

We have, 

=> y = (tan x)^{log x} + cos² (π/4)

=> $y=e^{log(tanx)^{logx}} +cos^2(\frac{π}{4})$

=> $y=e^{logxlog(tanx)} +cos^2(\frac{π}{4})$

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=\frac{d}{dx}[e^{logxlog(tanx)} +cos^2(\frac{π}{4})]$

=> $\frac{dy}{dx}=(e^{logxlog(tanx)})[logx(\frac{1}{tanx})(sec^2x)+log(tanx)(\frac{1}{x})] +0$

=> $\frac{dy}{dx}=(e^{logxlog(tanx)})[\frac{logxsec^2x}{tanx}+\frac{log(tanx)}{x}]$

=> $\frac{dy}{dx}=(tanx)^{logx}[\frac{logxsec^2x}{tanx}+\frac{log(tanx)}{x}]$

问题 31. 求 dy/dx 时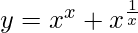$y=x^x+x^{\frac{1}{x}}$ .

解决方案：

We have,

=> $y=x^x+x^{\frac{1}{x}}$

=> $y=e^{logx^{x}} + e^{logx^{\frac{1}{x}}}$

=> $y=e^{xlogx} + e^{\frac{1}{x}logx}$

On differentiating both sides with respect to x, we get,

=> $\frac{dy}{dx}=\frac{d}{dx}[e^{xlogx} + e^{\frac{1}{x}logx}]$

=> $\frac{dy}{dx}=(e^{xlogx})[x(\frac{1}{x})+logx] + (e^{\frac{1}{x}logx})[(\frac{1}{x})(\frac{1}{x})+logx(\frac{-1}{x^2})]$

=> $\frac{dy}{dx}=(e^{xlogx})(1+logx) + (e^{\frac{1}{x}logx})[\frac{1}{x^2}-\frac{logx}{x^2}]$

=> $\frac{dy}{dx}=(e^{xlogx})(1+logx) + (e^{\frac{1}{x}logx})(\frac{1-logx}{x^2})$

=> $\frac{dy}{dx}=x^x(1+logx) + x^{\frac{1}{x}}(\frac{1-logx}{x^2})$

问题 32. 当 y = (log x) ^x + x ^logx时求 dy/dx。

解决方案：

We have, 

=> y = (log x)^x+ x^logx

Let u = (log x)^x and v = x^logx. Therefore, y = u + v.

Now, u = (log x)^x

On taking log of both the sides, we get,

=> log u = log (log x)^x

=> log u = x log (log x)

On differentiating both sides with respect to x, we get,

=> $\frac{1}{u}\frac{du}{dx}=\frac{d}{dx}[x log (log x)]$

=> $\frac{1}{u}\frac{du}{dx}=[x(\frac{1}{logx})(\frac{1}{x})+log(logx)]$

=> $\frac{1}{u}\frac{du}{dx}=\frac{1}{logx}+log(logx)$

=> $\frac{du}{dx}=u[\frac{1}{logx}+log(logx)]$

=> $\frac{du}{dx}=(logx)^x[\frac{1}{logx}+log(logx)]$

=> $\frac{du}{dx}=(logx)^x[\frac{1+logxlog(logx)}{logx}]$

=> $\frac{du}{dx}=(logx)^{x-1}[1+logxlog(logx)]$

Also, v = x^logx

On taking log of both the sides, we get,

=> log v = log x^logx

=> log v = log x (log x)

=> log v = (log x)²

On differentiating both sides with respect to x, we get,

=> $\frac{1}{v}\frac{dv}{dx}=\frac{d}{dx}[(log x)^2]$

=> $\frac{1}{v}\frac{dv}{dx}=2(logx)(\frac{1}{x})$

=> $\frac{dv}{dx}=v(\frac{2logx}{x})$

=> $\frac{dv}{dx}=x^{logx}(\frac{2logx}{x})$

=> $\frac{dv}{dx}=2logx.x^{logx-1}$

Now, y = u + v

=> $\frac{dy}{dx}=\frac{du}{dx}+\frac{dv}{dx}$

=> $\frac{dy}{dx}=(logx)^{x-1}[1+logxlog(logx)]+2logx.x^{logx-1}$

问题 33. 如果 x ¹³ y ⁷ = (x+y) ²⁰ ，证明$\frac{dy}{dx}=\frac{y}{x}$ .

解决方案：

We have, 

=> x¹³y⁷ = (x+y)²⁰

On taking log of both the sides, we get,

=> log x¹³y⁷ = log (x+y)²⁰

=> log x¹³ + log y⁷ = log (x+y)²⁰

=> 13 log x + 7 log y = 20 log (x+y)

On differentiating both sides with respect to x, we get,

=> $13(\frac{1}{x})+7(\frac{1}{y})(\frac{dy}{dx})=20(\frac{1}{x+y})(1+\frac{dy}{dx})$

=> $\frac{13}{x}+\frac{7}{y}\frac{dy}{dx}=\frac{20}{x+y}(1+\frac{dy}{dx})$

=> $\frac{13}{x}+\frac{7}{y}\frac{dy}{dx}=\frac{20}{x+y}+\frac{20}{x+y}\frac{dy}{dx}$

=> $\frac{7}{y}\frac{dy}{dx}-\frac{20}{x+y}\frac{dy}{dx}=\frac{20}{x+y}-\frac{13}{x}$

=> $\frac{dy}{dx}(\frac{7}{y}-\frac{20}{x+y})=\frac{20x-13x-13y}{x(x+y)}$

=> $\frac{dy}{dx}(\frac{7x+7y-20y}{y(x+y)})=\frac{7x-13y}{x(x+y)}$

=> $\frac{dy}{dx}(\frac{7x-13y}{y(x+y)})=\frac{7x-13y}{x(x+y)}$

=> $\frac{dy}{dx}=\frac{y}{x}$

Hence proved.

问题 34. 如果 x ¹⁶ y ⁹ = (x ² + y) ¹⁷ ，证明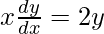$x\frac{dy}{dx}=2y$ .

解决方案：

We have, 

=> x¹⁶y⁹ = (x² + y)¹⁷

On taking log of both the sides, we get,

=> log x¹⁶y⁹ = log (x² + y)¹⁷

=> log x¹⁶ + log y⁹ = log (x² +y)¹⁷

=> 16 log x + 9 log y = 17 log (x² + y)

On differentiating both sides with respect to x, we get,

=> $16(\frac{1}{x})+9(\frac{1}{y})(\frac{dy}{dx})=17(\frac{1}{x^2+y})(2x+\frac{dy}{dx})$

=> $\frac{16}{x}+\frac{9}{y}\frac{dy}{dx}=\frac{34x}{x^2+y}+\frac{17}{x^2+y}\frac{dy}{dx}$

=> $\frac{9}{y}\frac{dy}{dx}-\frac{17}{x^2+y}\frac{dy}{dx}=\frac{34x}{x^2+y}-\frac{16}{x}$

=> $(\frac{9}{y}-\frac{17}{x^2+y})\frac{dy}{dx}=\frac{34x^2-16x^2-16y}{x(x^2+y)}$

=> $(\frac{9x^2+9y-17y}{y(x^2+y)})\frac{dy}{dx}=\frac{34x^2-16x^2-16y}{x(x^2+y)}$

=> $(\frac{9x^2-8y}{y(x^2+y)})\frac{dy}{dx}=\frac{18x^2-16y}{x(x^2+y)}$

=> $(\frac{9x^2-8y}{y})\frac{dy}{dx}=\frac{2(9x^2-8y)}{x}$

=> $\frac{dy}{dx}=\frac{2y}{x}$

=> $x\frac{dy}{dx}=2y$

Hence proved.

问题 35. 如果 y = sin x ^x ，证明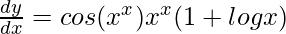$\frac{dy}{dx}=cos(x^x)×x^x(1+logx)$ .

解决方案：

We have, 

=> y = sin x^x 

Let u = x^x. Now y = sin u.

On taking log of both the sides, we get,

=> log u = log x^x

=> log u = x log x

On differentiating both sides with respect to x, we get,

=> $\frac{1}{u}\frac{du}{dx}=x(\frac{1}{x})+logx$

=> $\frac{1}{u}\frac{du}{dx}=1+logx$

=> $\frac{du}{dx}=u(1+logx)$

=> $\frac{du}{dx}=x^x(1+logx)$

Now, y = sin u

=> $\frac{dy}{dx}=cosu\frac{du}{dx}$

=> $\frac{dy}{dx}=cosu×x^x(1+logx)$

=> $\frac{dy}{dx}=cosx^x×x^x(1+logx)$

Hence proved.

问题 36. 如果 x ^x + y ^x = 1，证明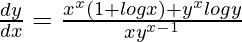$\frac{dy}{dx}=\frac{x^x(1+logx)+y^xlogy}{xy^{x-1}}$ .

解决方案：

We have, 

=> x^x + y^x = 1

=> $e^{logx^x} + e^{logy^x} = 1$

=> $e^{xlogx} + e^{xlogy} = 1$

On differentiating both sides with respect to x, we get,

=> $(e^{xlogx})[x(\frac{1}{x})+logx] + (e^{xlogy})[x(\frac{1}{y})(\frac{dy}{dx})+logy] = 0$

=> $(e^{xlogx})(1+logx) + (e^{xlogy})[(\frac{x}{y})(\frac{dy}{dx})+logy] = 0$

=> $x^x(1+logx) + y^x[(\frac{x}{y})(\frac{dy}{dx})+logy] = 0$

=> $x^x(1+logx) + xy^{x-1}\frac{dy}{dx}+y^xlogy = 0$

=> $xy^{x-1}\frac{dy}{dx} = -[x^x(1+logx)+y^xlogy ]$

=> $\frac{dy}{dx} = \frac{-[x^x(1+logx)+y^xlogy]}{xy^{x-1}}$

Hence proved.

问题 37. 如果 x ^y × y ^x = 1，证明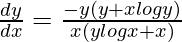$\frac{dy}{dx}=\frac{-y(y+xlogy)}{x(ylogx+x)}$ .

解决方案：

We have, 

=> x^y × y^x = 1

On taking log of both the sides, we get,

=> log (x^y × y^x) = log 1

=> log x^y + log y^x = log 1

=> y log x + x log y = log 1

On differentiating both sides with respect to x, we get,

=> $y(\frac{1}{x})+logx(\frac{dy}{dx})+x(\frac{1}{y})(\frac{dy}{dx})+log y = 0$

=> $\frac{y}{x}+logx(\frac{dy}{dx})+(\frac{x}{y})(\frac{dy}{dx})+log y = 0$

=> $(\frac{y}{x}+logy)+(logx+\frac{x}{y})(\frac{dy}{dx}) = 0$

=> $(\frac{y+xlogy}{x})+(\frac{ylogx+x}{y})(\frac{dy}{dx}) = 0$

=> $(\frac{ylogx+x}{y})(\frac{dy}{dx})= -(\frac{y+xlogy}{x})$

=> $\frac{dy}{dx}=\frac{-y(y+xlogy)}{x(ylogx+x)}$

Hence proved.

问题 38. 如果 x ^y + y ^x = (x+y) ^x+y ，求 dy/dx。

解决方案：

We have, 

=> x^y + y^x = (x+y)^x+y

=> $e^{logx^y} + e^{logy^x} = e^{log(x+y)^{x+y}}$

=> $e^{ylogx} + e^{xlogy} = e^{(x+y)log(x+y)}$

On differentiating both sides with respect to x, we get,

=> $(e^{ylogx})[y(\frac{1}{x})+logx(\frac{dy}{dx})] + (e^{xlogy})[x(\frac{1}{y})(\frac{dy}{dx})+logy]=(e^{(x+y)log(x+y)})[(x+y)(\frac{1}{x+y})(1+\frac{dy}{dx})+log(x+y)(1+\frac{dy}{dx})]$

=> $e^{ylogx}[\frac{y}{x}+logx(\frac{dy}{dx})] + (e^{xlogy})[(\frac{x}{y})(\frac{dy}{dx})+logy]=(e^{(x+y)log(x+y)})[1+\frac{dy}{dx}+log(x+y)(1+\frac{dy}{dx})]$

=> $x^y[\frac{y}{x}+logx(\frac{dy}{dx})] + y^x[(\frac{x}{y})(\frac{dy}{dx})+logy]=(x+y)^{x+y}[1+\frac{dy}{dx}+log(x+y)(1+\frac{dy}{dx})]$

=> $\frac{dy}{dx}[x^ylogx+xy^{x-1}-(x+y)^{x+y}(1+log(x+y))]=(x+y)^{x+y}(1+log(x+y))-yx^{y-1}-y^xlogy$

=> $\frac{dy}{dx}=\frac{(x+y)^{x+y}(1+log(x+y))-yx^{y-1}-y^xlogy}{x^ylogx+xy^{x-1}-(x+y)^{x+y}(1+log(x+y))}$

问题 39. 如果 x ^m y ⁿ = 1，证明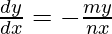$\frac{dy}{dx}=-\frac{my}{nx}$ .

解决方案：

We have, 

=> x^m yⁿ = 1

On taking log of both the sides, we get,

=> log (x^m yⁿ)= log 1

=> log x^m + log yⁿ = log 1

=> m log x + n log y = log 1

On differentiating both sides with respect to x, we get,

=> $m(\frac{1}{x})+n(\frac{1}{y})(\frac{dy}{dx}) = 0$

=> $\frac{m}{x}+\frac{n}{y}(\frac{dy}{dx}) = 0$

=> $\frac{n}{y}(\frac{dy}{dx}) = -\frac{m}{x}$

=> $\frac{dy}{dx}= -\frac{my}{xn}$

Hence proved.

问题 40. 如果 y ^x = e ^y−x ，证明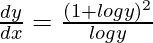$\frac{dy}{dx}=\frac{(1+logy)^2}{logy}$ .

解决方案：

We have, 

=> y^x = e^y−x

On taking log of both the sides, we get,

=> log y^x = log e^y−x

=> x log y = (y − x) log e

=> x log y = y − x

On differentiating both sides with respect to x, we get,

=> $x(\frac{1}{y})(\frac{dy}{dx})+logy=\frac{dy}{dx}−1$

=> $\frac{x}{y}\frac{dy}{dx}+logy=\frac{dy}{dx}−1$

=> $(\frac{x}{y}-1)\frac{dy}{dx}=−1-logy$

=> $(\frac{x}{y}-1)\frac{dy}{dx}=−(1+logy)$

=> $(\frac{y}{1+logy})\frac{dy}{dx}=−(1+logy)$

=> $(\frac{1-1-logy}{1+logy})\frac{dy}{dx}=−(1+logy)$

=> $\frac{dy}{dx}=−\frac{(1+logy)^2}{-logy}$

=> $\frac{dy}{dx}=\frac{(1+logy)^2}{logy}$

Hence proved.