第 12 课 RD Sharma 解决方案 - 第 29 章飞机 - 练习 29.9
问题1.求点的距离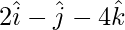 从飞机上
从飞机上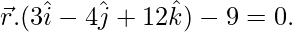
解决方案:
As we know the distance of a point ![]() from a plane
from a plane ![]() is given by:
is given by:
![]()
Here, ![]() and
and ![]() is the plane.
is the plane.
Hence, 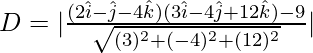
⇒ ![]()
= |-47/13| units
= 47/13 units
Hence, the distance of the point from the plane is 47/13 units.
问题 2. 证明点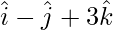 和
和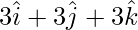 与飞机等距
与飞机等距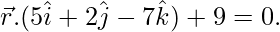
解决方案:
As we know the distance of a point ![]() from a plane
from a plane ![]() is given by:
is given by:
![]()
Let D1 be the distance of ![]() from the plane
from the plane ![]()
⇒ 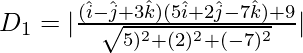
= ![]()
= 9/√78 units …….(1)
Now, let D2 be the distance between point ![]() and the plane
and the plane ![]() .
.
⇒ 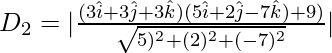
= ![]()
= 9/√78 units ……(2)
From eq(1) and (2), we have
The given points are equidistant from the given plane.
问题 3. 求点 (2, 3, -5) 到平面 x + 2y - 2z - 9 = 0 的距离。
解决方案:
As we know the distance is given by:
![]()
⇒ 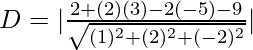
= ![]()
= 9/√9
D = 3 units.
问题 4. 找出平行于平面 x + 2y - 2z + 8 = 0 的平面方程,这些平面与点 (2, 1, 1) 的距离为 2 个单位。
解决方案:
The equation of a plane parallel to the given plane is x + 2y − 2z + p = 0.
As we know that the distance between a point and plane is given by:
![]()
Given, D = 2 units. Hence,
![]()
⇒ ![]()
On squaring both sides, we have
![]()
⇒ 36 = (2 + p)2
⇒ 2 + p = 6 or 2 + p = −6
⇒ p = 4 or p = −8
Hence, the equations of the required planes are:
x + 2y − 2z + 4 = 0 and x + 2y − 2z − 8 = 0.
问题 5. 证明点 (1, 1, 1) 和 (-3, 0, 1) 与平面 3x + 4y − 12z +13 = 0 等距。
解决方案:
We know that the distance between a point and plane is given by:
![]()
Let D1 be the distance of the point (1,1,1) from the plane.
⇒ 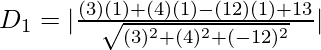
= 8/13 units
Let D2 be the distance of the point.
⇒ 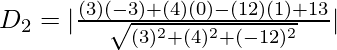
= 8/13 units
Hence, the points are equidistant from the plane.
问题 6. 找出平行于平面 x - 2y + 2z - 3 = 0 的平面方程,这些平面距离点 (2, 1, 1) 有一个单位距离。
解决方案:
Equation of a plane parallel to the given plane is x − 2y + 2z + p = 0.
As we know that the distance between a point and plane is given by:
![]()
Given, D = 1 units. Hence,
![]()
⇒ ![]()
On squaring both sides, we have
![]()
⇒ 9 = (1 + p)2
⇒ 1 + p = 3 or 1 + p = −3
⇒ p = 2 or p = −4
Hence, the equations of the required planes are:
x − 2y + 2z + 2 = 0 and x − 2y + 2z − 4 = 0.
问题 7. 求点 (2, 3, 5) 到 xy 平面的距离。
解决方案:
As we know the distance of the point from the plane is given by:
D = ![]()
= 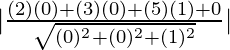
= ![]()
D = 5 units
问题 8. 求点 (3, 3, 3) 到平面的距离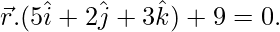
解决方案:
As we know the distance of a point ![]() from a plane
from a plane ![]() is given by:
is given by:
D = ![]()
= ![]()
= ![]()
D = 9/√78 units.
问题 9. 如果点 (1, 1, 1) 到原点和平面 x - y + z + p = 0 的距离的乘积为 5,求 p。
解决方案:
The distance of the point (1, 1, 1) from the origin is ![]()
Distance of (1, 1, 1) from the plane is ![]()
Given: ![]()
⇒ |1 + p| = 5
⇒ p = 4 or −6.
问题 10. 求与平面 3x - 4y + 12 = 6 和 4x + 3z = 7 等距的所有点的集合的方程。
解决方案:
![]()
![]()
= ![]()
Now, ![]()
= ![]()
Given, D1 = D2
⇒ ![]()
Hence, the equations become
37x1 + 20y1 − 21z1 − 61 = 0 and 67x1 + 20y1 + 99z1 − 121 = 0.
问题 11. 求点 (7, 2, 4) 与由点 A(-2, -3, 5) 和 C(5, 3, -3) 确定的平面之间的距离。
解决方案:
The equations of the plane are given as:
−4a − 8b + 8c = 0 and 3a − 2b + 0c = 0
Solving the above set using cross multiplication method, we get
![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ a = 2p, b = 3p, c = 4p
Thus, the equation of the plane becomes 2x + 3y + 4z − 7 = 0.
and, distance = √29 units.
问题 12. 平面在坐标轴上分别截距 -6、3、4。从它的原点找到垂线的长度。
解决方案:
Since the plane makes intercepts −6, 3, 4, the equation becomes:
![]()
Let p be the distance of perpendicular from the origin to the plane.
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ 1/p2 = 29/144
⇒ p2 = 144/29
⇒ p = 12/√29 units.