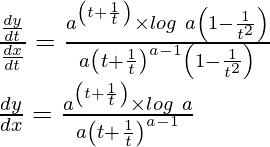第 12 类 RD Sharma 解决方案 - 第 11 章微分 - 练习 11.7 |设置 2
问题 11. 查找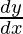 , 什么时候
, 什么时候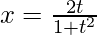 和
和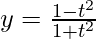
解决方案:
Here,
![]()
Differentiating it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(2t)-2t\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(2)-2t(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{2+2t^2-4t^2}{(1+t^2)^2}\right]\\ =\left[\frac{2+2t^2-4t^2}{(1+t^2)^2}\right]\\ =\left[\frac{2-2t^2}{(1+t^2)^2}\right]\\ \frac{dx}{dt}=\frac{2(1-t^2)}{(1+t^2)^2}\ \ \ \ \ ....(1)](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_4.jpg)
and,
![]()
Differentiating it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(1-t^2)-(1-t^2)\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(-2t)-(1-t^2)(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{-2t-2t^3-2t+2t^3}{(1+t^2)^2}\right]\\ \frac{dy}{dt}=\frac{-4t}{(1+t^2)^2}\ \ \ \ \ ....(2)](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_6.jpg)
Dividing equation (2) by (1)
![Rendered by QuickLaTeX.com \frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{-4t}{(1+t^2)^2}\times\frac{(1+t^2)^2}{2(1-t^2)}\\ =\frac{-2t}{1-t^2}\\ \frac{dy}{dx}=-\frac{x}{y}\ \ \ \ \left[Since,\ \frac{x}{y}=\frac{2t}{1+t^2}\times\frac{1+t^2}{1-t^2}=\frac{2t}{1-t^2}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_7.jpg)
问题 12. 查找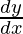 , 什么时候
, 什么时候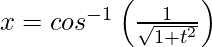 和
和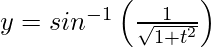
解决方案:
Here,
![]()
Differentiating it with respect to t using chain rule,
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\frac{-1}{\sqrt{1-\left(\frac{1}{1+t^2}\right)}^2}\frac{d}{dt}\left(\frac{1}{\sqrt{1+t^2}}\right)\\ =\frac{-1}{\sqrt{1-\frac{1}{(1+t^2)}}}\left[\frac{-1}{2(1+t^2)^{\frac{3}{2}}}\right]\frac{d}{dt}(1+t^2)\\ =\frac{(1+t^2)^{\frac{1}{2}}}{\sqrt{1+t^2-1}}\times\frac{-1}{2(1+t^2)^{\frac{3}{2}}}(2t)\\ =\frac{-t}{\sqrt{t^2}\times(1+t^2)}\\ \frac{dx}{dt}=\frac{-1}{1+t^2}\ \ \ \ \ ....(1)](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_12.jpg)
Now,
![]()
Differentiating it with respect to t using chain rule,
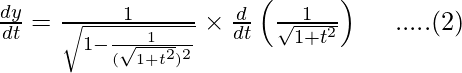
Dividing equation (2) by (1)
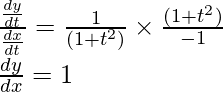
问题 13. 查找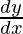 , 什么时候
, 什么时候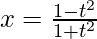 和
和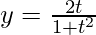
解决方案:
Here,
![]()
Differentiating it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(1-t^2)-(1-t^2)\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(-2t)-(1-t^2)(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{-2t-2t^3-2t+2t^3}{(1+t^2)^2}\right]\\ \frac{dx}{dt}=\frac{-4t}{(1+t^2)^2}\ \ \ \ \ ....(1)](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_20.jpg)
and,
![]()
Differentiating it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(2t)-2t\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(2)-2t(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{2+2t^2-4t^2}{(1+t^2)^2}\right]\\ \frac{dx}{dt}=\frac{2(1-t^2)}{(1+t^2)^2}\ \ \ \ \ ....(2)](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_22.jpg)
问题 14. 如果 x = 2co sθ – cos2θ 和 y = 2sinθ – sin2θ ,证明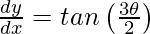
解决方案:
Here,
x = 2cosθ – cos2θ
Differentiating it with respect to θ using chain rule,
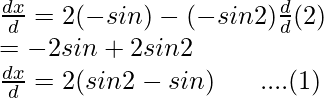
and,
y = 2sinθ – sin2θ
Differentiating it with respect to θ using chain rule,
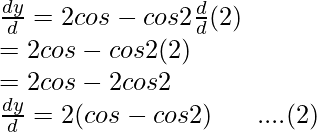
Dividing equation (2) by equation (1),
![Rendered by QuickLaTeX.com \frac{\frac{dy}{dθ}}{\frac{dx}{dθ}}=\frac{2(cosθ -cos2θ )}{2(sin2θ - sinθ )}\\ =\frac{cosθ -cos2θ}{sin2θ -sinθ}\\ \frac{dy}{dx}=\frac{-2sin\left(\frac{θ +2θ}{2}\right)sin\left(\frac{θ -2θ}{2}\right)}{2cos\left(\frac{2θ +θ}{2}\right)sin\left(\frac{2θ -θ}{2}\right)}\ \ \ \ \left[Since,\ sinA-sinB=2cos\left(\frac{A+B}{2}\right)sin\left(\frac{A-B}{2}\right),\ \ cosA-cosB=-2sin\left(\frac{A+B}{2}\right)sin\left(\frac{A-B}{2}\right)\right]\\ =\frac{-sin\left(\frac{3θ )}{2}\right)\left(sin\left(\frac{-θ}{2}\right)\right)}{cos\left(\frac{3θ}{2}\right)sin\left(\frac{θ}{2}\right)}\\ =\frac{sin\left(\frac{3θ}{2}\right)}{cos\left(\frac{3θ}{2}\right)}\\ \frac{dy}{dx}=tan\left(\frac{3θ}{2}\right)](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_26.jpg)
问题 15. 如果 x = e cos2t和 y = e sin2t证明, 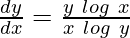
解决方案:
Here,
x = ecos2t
Differentiating it with respect to t using chain rule,
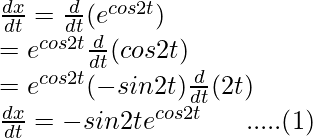
and,
y = esin2t
Differentiating it with respect to t using chain rule,
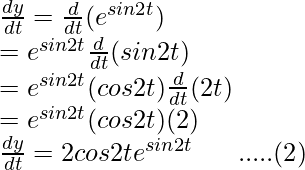
Dividing equation (2) by (1)
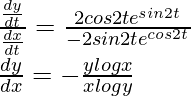
![]()
问题 16. 如果 x = cos t 和 y = sin t,证明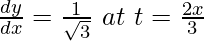
解决方案:
Here,
x = cos t
Differentiating it with respect to t,
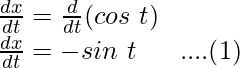
and,
y = sin t
Differentiating it with respect to t,
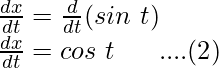
Dividing equation (2) by (1),
![Rendered by QuickLaTeX.com \frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{cos\ t}{-sin\ t}\\ \frac{dy}{dx}=-cot\ t\\ \left(\frac{dy}{dx}\right)=-cot\left(\frac{2\pi}{3}\right)\\ =-cot\left(\pi-\frac{\pi}{3}\right)\\ =-\left[-cot\left(\frac{\pi}{3}\right)\right]\\ =cot\left(\frac{\pi}{3}\right)\\ \frac{dy}{dx}=\frac{1}{\sqrt3}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_35.jpg)
问题 17. 如果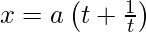 和
和 , 证明
, 证明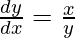
解决方案:
Here,
![]()
Differentiating it with respect to t,
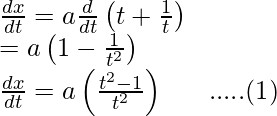
and,
![]()
Differentiating it with respect to t,
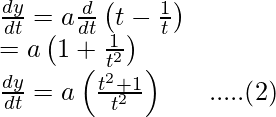
Dividing equation (2) by (1)
![Rendered by QuickLaTeX.com \frac{\frac{dy}{dt}}{\frac{dx}{dt}}=a\frac{(t^2+1)}{t^2}\times\frac{t^2}{a(t^2-1)}\\ \frac{dy}{dx}=\frac{t^2+1}{t^2-1}\\ \frac{dy}{dx}=\frac{x}{y}\ \ \ \ \ \ \left[Since,\ \frac{x}{y}=\frac{a(t^2+1)}{t}\times\frac{t}{a(t^2-1)}=\left(\frac{t^2+1}{t^2-1}\right)\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_43.jpg)
问题 18. 如果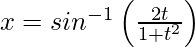 和
和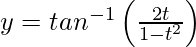 , -1 < 1 < 1,证明
, -1 < 1 < 1,证明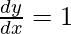
解决方案:
Here,
![]()
Put t = tan θ
![Rendered by QuickLaTeX.com x=sin^{-1}\left(\frac{2tanθ}{1+tan^2θ}\right)\\ =sin^{-1}(sin2θ )\\ =2θ \ \ \ \ \ \left[Since,\ sin\ 2x=\frac{2tan\ x}{1+tan^2x}\right]\\ x=2(tan^{-1}t)\ \ \ \ \ [Since,\ t=sin\ θ ]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_48.jpg)
Differentiating it with respect to t,
![]()
Further,
![]()
Put t = tan θ
![Rendered by QuickLaTeX.com y=tan^{-1}\left(\frac{2tanθ}{1+tan^2θ}\right)\\ =tan^{-1}(tan2θ )\\ =2θ \ \ \ \ \ \left[Since,\ tan\ 2x=\frac{2tan\ x}{1-tan^2x}\right]\\ y=2tan^{-1}t\ \ \ \ \ [Since,\ t=tan\ θ ]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_51.jpg)
Differentiating it with respect to t,
![]()
Dividing equation (2) by (1),
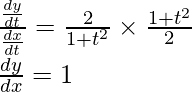
问题 19. 如果 x 和 y 通过方程参数连接,不消去参数,求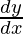 , 什么时候:
, 什么时候: 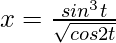 ,
, 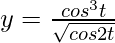
解决方案:
Here, the given equations are![]() and
and![]()
Thus,
![Rendered by QuickLaTeX.com \frac{dx}{dt}\frac{d}{dt}\left[\frac{sin^3t}{\sqrt{cos2t}}\right]\\ =\frac{\sqrt{cos2t}.\frac{d}{dt}(sin^3t)-sin^3t.\frac{d}{dt}\sqrt{cos2t}}{cos2t}\\ =\frac{\sqrt{cos2t}.3sin^2t.\frac{d}{dt}(sin\ t)-sin^3t\times\frac{1}{2\sqrt{cos\ 2t}}.\frac{d}{dt}(cos2t)}{cos2t}\\ =\frac{3\sqrt{cos\ 2t}.sin^2t\ cos\ t-\frac{sin^3t}{2\sqrt{cos\ 2t}}.(-2sin\ 2t)}{cos\ 2t}\\ =\frac{3cos\ 2t\ sin^2tcos\ t+sin^3tsin\ 2t}{cos\ 2t\sqrt{cos\ 2t}}\\ \frac{dy}{dt}=\frac{d}{dt}\left[\frac{cos^3t}{\sqrt{cos\ 2t}}\right]\\ =\frac{\sqrt{cos\ 2t}.\frac{d}{dt}(cos^3t)-cos^3t.\frac{d}{dt}(\sqrt{cos\ 2t})}{cos\ 2t}\\ =\frac{-3cos\ 2t.cos^2t.sin\ t+cos^3t\ sin\ 2t}{cos\ 2t.\sqrt{cos\ 2t}}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_59.jpg)
Therefore,
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{-3cos\ 2t.cos^2t. sin\ t+cos^3t\ sin\ 2t}{3cos\ 2t\ sin^2t\ cos\ t+sin^3t\ sin\ 2t}\\ =\frac{-3cos\ 2t\ cos^2t.sin\ t+cos^3t(2sin\ t\ cos\ t)}{3cos\ 2t\ sin^2t\ cos\ t+sin^3t(2sin\ t+2sin^3t)}\\ =\frac{[-3(2cos^2t-1)cos\ t+2cos^3t]}{[3(1-2sin^2t)sin\ t+2sin^3t]}\ \ \ \ \ \ \ [cos\ 2t=(2cos^2t-1),\ cos\ 2t=(1-2sin^2t)]\\ =\frac{-4cos^3t+3cos\ t}{3sin\ t-4sin^3\ t}\\ =\frac{-cos\ 3t}{sin\ 3t}\ \ \ \ \ \ [cos\ 3t=4cos^3t3cos\ t,\ sin\ 3t=3sin\ t-4sin^3t]\\ =-cot3t](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_11_Differentiation_%E2%80%93_Exercise_11.7_%7C_Set_2_60.jpg)
问题 20. 如果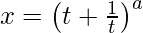 和
和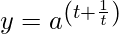 , 找
, 找
解决方案:
Here,
![]()
Differentiating it with respect to t using chain rule,
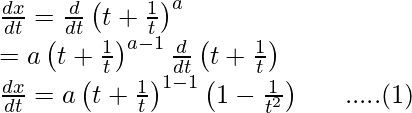
And,
![]()
Differentiating it with respect to t using chain rule,
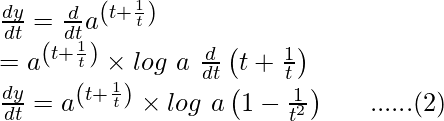
Dividing equation (2) by (1)