问题1:从第一原理中得出以下函数的派生:
(i)-x
解决方案:
f(x) = -x
f(x+h) = -(x+h)
From the first principle,
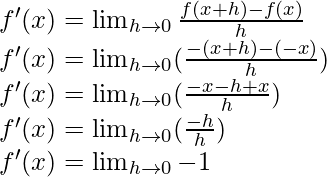
f'(x) = -1
(ii)(-x) -1
解决方案:
f(x) = (-x)-1 = ![]()
f(x+h) = (-(x+h))-1 = ![]()
From the first principle,
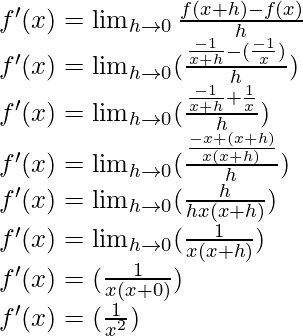
(iii)罪(x + 1)
解决方案:
f(x) = sin(x+1)
f(x+h) = sin((x+h)+1)
From the first principle,
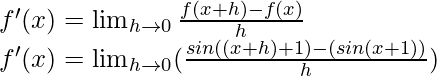
Using the trigonometric identity,
sin A – sin B = 2 cos ![]() sin
sin ![]()
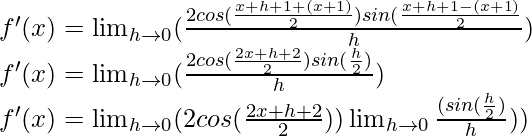
Multiply and divide by 2, we have
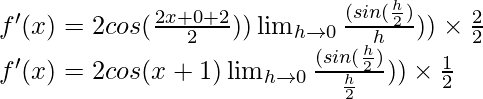
f'(x) = cos (x+1) (1)
f'(x) = cos (x+1)
(iv) 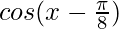
解决方案:
Here, 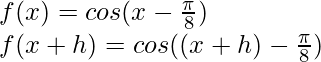
From the first principle,
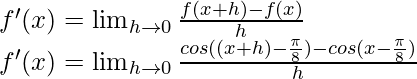
Using the trigonometric identity,
cos a – cos b = -2 sin ![]() sin
sin ![]()
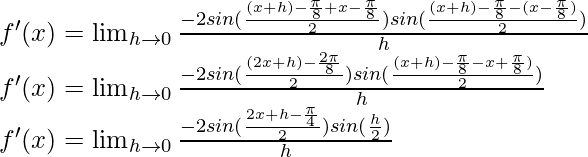
Multiplying and diving by 2,
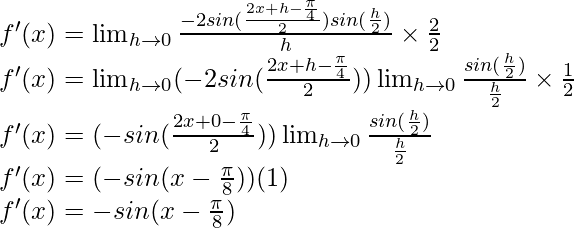
找到以下函数的导数(可以理解,a,b,c,d,p,q,r和s是固定的非零常数,m和n是整数):
问题2:(x + a)
解决方案:
f(x) = x+a
Taking derivative both sides,
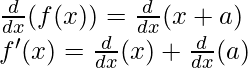
As, the derivative of xn is nxn-1 and derivative of constant is 0.
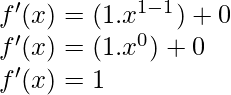
问题3: 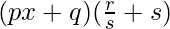
解决方案:
![]()
Taking derivative both sides,
![]()
Using the product rule, we have
(uv)’ = uv’+u’v
![]()
As, the derivative of xn is nxn-1 and derivative of constant is 0.

问题4:(ax + b)(cx + d) 2
解决方案:
f(x) = (ax+b) (cx+d)2
Taking derivative both sides,
![]()
Using the product rule, we have
(uv)’ = uv’+u’v
![]()
As, the derivative of xn is nxn-1 and derivative of constant is 0.
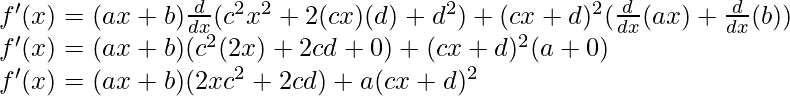
问题5: 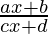
解决方案:
![]()
Taking derivative both sides,
![]()
Using the quotient rule, we have
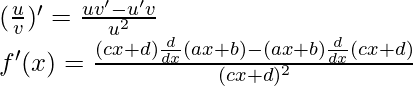
As, the derivative of xn is nxn-1 and derivative of constant is 0.
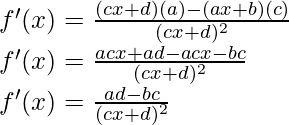
问题6: 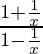
解决方案:
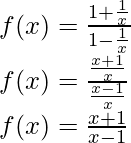
Taking derivative both sides,
![]()
Using the quotient rule, we have
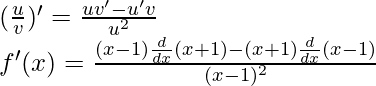
As, the derivative of xn is nxn-1 and derivative of constant is 0.
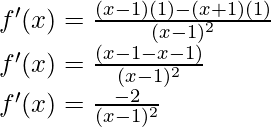
问题7: 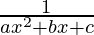
解决方案:
![]()
Taking derivative both sides,
![]()
Using the quotient rule, we have
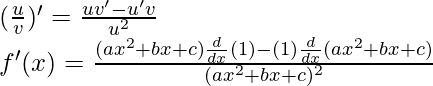
As, the derivative of xn is nxn-1 and derivative of constant is 0.

问题8: 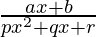
解决方案:
![]()
Taking derivative both sides,
![]()
Using the quotient rule, we have
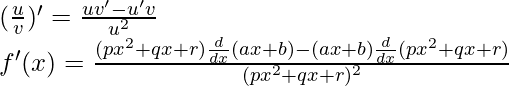
As, the derivative of xn is nxn-1 and derivative of constant is 0.
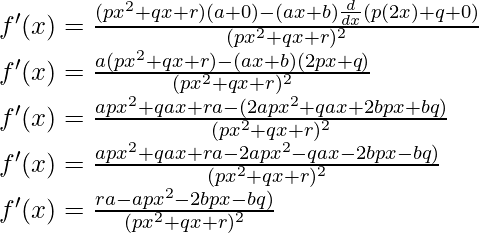
问题9: 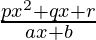
解决方案:
![]()
Taking derivative both sides,
![]()
Using the quotient rule, we have
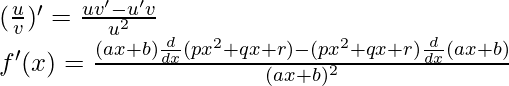
As, the derivative of xn is nxn-1 and derivative of constant is 0.
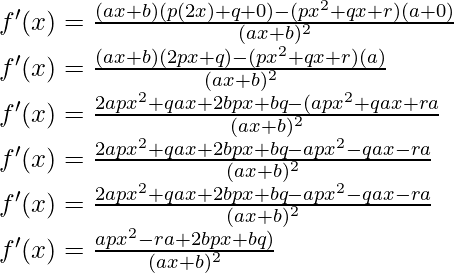
问题10: 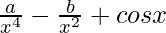
解决方案:
![]()
Taking derivative both sides,
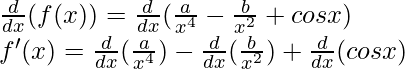
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = a \frac{d}{dx}(x^{-4}) - b\frac{d}{dx}(x^{-2})+(- sin x)\\ f'(x) = a (-4x^{-4-1}) - b((-2)x^{-2-1})+(- sin x)\\ f'(x) = a (-4x^{-5}) - b((-2)x^{-3})+(- sin x)\\ f'(x) = -[4ax^{-5} - 2bx^{-3} + sin x]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2011%20NCERT%20Solutions-%20Chapter%2013%20Limits%20And%20Derivatives%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%2013%20%7C%20Set%201_54.jpg)
问题11: 
解决方案:
![]()
Taking derivative both sides,
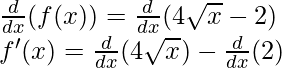
As, the derivative of xn is nxn-1 and derivative of constant is 0.

问题12:(ax + b) n
解决方案:
f(x) = (ax+b)n
f(x+h) = (a(x+h)+b)n
f(x+h) = (ax+ah+b)n
From the first principle,
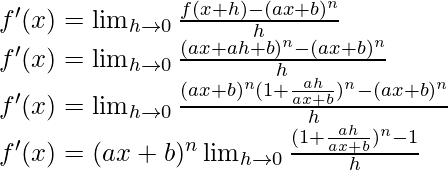
Using the binomial expansion, we have
![Rendered by QuickLaTeX.com f'(x) = (ax+b)^n \lim_{h \to 0} \frac{[1+n(\frac{ah}{ax+b}+\frac{n(n-1)}{2!}(\frac{ah}{(ax+b)^2}+.....]-1}{h}\\ f'(x) = (ax+b)^n \lim_{h \to 0} \frac{[n(\frac{ah}{ax+b}+\frac{n(n-1)a^2h^2}{2!(ax+b)^2}+.................]}{h}\\ f'(x) = (ax+b)^n \lim_{h \to 0} [n(\frac{a}{ax+b}+\frac{n(n-1)a^2h}{2!(ax+b)^2}+.................]\\ f'(x) = (ax+b)^n [n(\frac{a}{ax+b}+\frac{n(n-1)a^2(0)}{2!(ax+b)^2}+0+0+0......]\\ f'(x) = (ax+b)^n (\frac{na}{ax+b})\\ f'(x) = na (ax+b)^{n-1}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2011%20NCERT%20Solutions-%20Chapter%2013%20Limits%20And%20Derivatives%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%2013%20%7C%20Set%201_60.jpg)
问题13:(ax + b) n (cx + d) m
解决方案:
f(x) = (ax+b)n (cx+d)m
Taking derivative both sides,
![]()
Using the product rule, we have
(uv)’ = uv’+u’v
![]()
Let’s take, g(x) = (cx+d)m
![]()
g(x+h) = (c(x+h)+d)m
g(x+h) = (cx+ch+d)m
From the first principle,
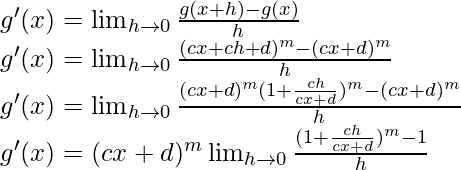
Using the binomial expansion, we have
![Rendered by QuickLaTeX.com g'(x) = (cx+d)^m \lim_{h \to 0} \frac{[1+m(\frac{ch}{cx+d}+\frac{m(m-1)}{2!}(\frac{ch}{(cx+d})^2+.....)]-1}{h}\\ g'(x) = (cx+d)^m \lim_{h \to 0} \frac{[m(\frac{ch}{cx+d}+\frac{m(nm-1)c^2h^2}{2!(cx+d)^2}+.................)]}{h}\\ g'(x) = (cx+d)^m \lim_{h \to 0} [m(\frac{c}{cx+d}+\frac{m(m-1)c^2h}{2!(cx+d)^2}+.................)]\\ g'(x) = (cx+d)^m [m(\frac{c}{cx+d}+\frac{m(m-1)c^2(0)}{2!(cx+d)^2}+0+0+0......)]\\ g'(x) = (cx+d)^m (\frac{mc}{cx+d})\\ g'(x) = mc (cx+d)^{m-1}](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2011%20NCERT%20Solutions-%20Chapter%2013%20Limits%20And%20Derivatives%20%E2%80%93%20Miscellaneous%20Exercise%20on%20Chapter%2013%20%7C%20Set%201_65.jpg)
So, as
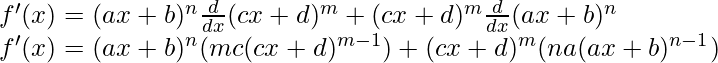
问题14:罪(x + a)
解决方案:
f(x) = sin(x+a)
f(x+h) = sin((x+h)+a)
From the first principle,
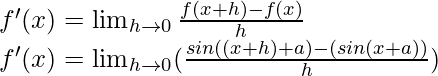
Using the trigonometric identity,
sin A – sin B = 2 cos ![]() sin
sin ![]()
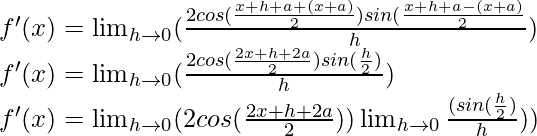
Multiply and divide by 2, we have
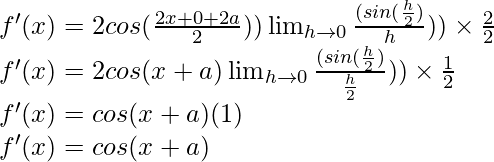
问题15:cosec x cot x
解决方案:
f(x) = cosec x cot x
Taking derivative both sides,
![]()
Using the product rule, we have
(uv)’ = uv’+u’v
![]()
f'(x) = cot x (-cot x cosec x) + (cosec x) (-cosec2 x)
f'(x) = – cot2 x cosec x – cosec3 x