在练习1至22中评估以下限制。
问题1: 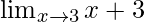
解决方案:
In ![]() , as x⇢3
, as x⇢3
Put x = 3, we get
![]() = 3+3
= 3+3
= 6
问题2: 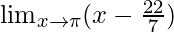
解决方案:
In ![]() , as x⇢π
, as x⇢π
Put x = π, we get
![]()
= ![]()
问题3: 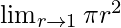
解决方案:
In ![]() , as r⇢1
, as r⇢1
Put r = 1, we get
![]()
= π
问题4: 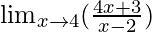
解决方案:
In ![]() , as x⇢4
, as x⇢4
Put x = 4, we get
![]()
= ![]()
问题5: 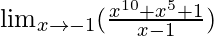
解决方案:
In ![]() , as x⇢-1
, as x⇢-1
Put x = -1, we get
![]()
= ![]()
= ![]()
问题6: 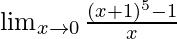
解决方案:
In ![]() , as x⇢0
, as x⇢0
Put x = 0, we get
![]()
As, this limit becomes undefined
Now, let’s take x+1=p and x = p-1, to make it equivalent to theorem.
![]()
As, x⇢0 ⇒ p⇢1
![]()
Here, n=5 and a = 1.
![]()
= 5(1)4
= 5
问题7: 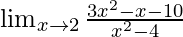
解决方案:
In ![]() , as x⇢2
, as x⇢2
Put x = 2, we get
![]()
As, this limit becomes undefined
Now, let’s Factorise the numerator and denominator, we get
![]()
= ![]()
Cancelling (x-2), we have
= ![]()
Put x = 2, we get
![]()
= ![]()
问题8: 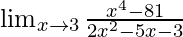
解决方案:
In ![]() , as x⇢3
, as x⇢3
Put x = 3, we get
![]()
As, this limit becomes undefined
Now, let’s Factorise the numerator and denominator, we get
![]()
= ![]()
= ![]()
Cancelling (x-3), we have
= ![]()
Put x = 3, we get
= ![]()
= ![]()
= ![]()
问题9: 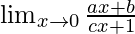
解决方案:
In ![]() , as x⇢0
, as x⇢0
Put x = 0, we get
![]()
= b
问题10: 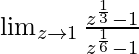
解决方案:
In 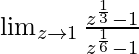 , as z⇢1
, as z⇢1
Put z = 1, we get
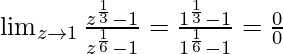
Let’s take ![]() = p and
= p and ![]() = p2,
= p2,
As, z⇢1 ⇒ p⇢1
= ![]()
Now, let’s Factorise the numerator, we get
= ![]()
Cancelling (p-1), we have
= ![]()
Put p = 1, we get
![]()
= 2
问题11: 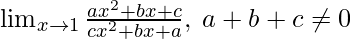
解决方案:
In ![]() , as x⇢1
, as x⇢1
Put x = 1, we get
![]()
= ![]()
= 1 (As it is given a+b+c≠0)
问题12: 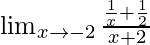
解决方案:
In ![]() , as x⇢-2
, as x⇢-2
Firstly, lets simplify the equation
![]()
Cancelling (x+2),we get
![]()
Put x = -2, we get
![]()
= ![]()
问题13: 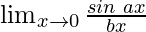
解决方案:
In ![]() , as x⇢0
, as x⇢0
Put x = 0, we get
![]()
As, this limit becomes undefined
Now, let’s multiply and divide the equation by a, to make it equivalent to theorem.
![]()
Hence, we have
![]()
= ![]()
= ![]()
As x⇢0, then ax⇢0
= ![]()
By using the theorem, we get
= ![]()
= ![]()
问题14: 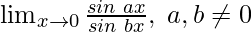
解决方案:
In ![]() , as x⇢0
, as x⇢0
Put x = 0, we get
![]()
As, this limit becomes undefined
Now, let’s multiply and divide the numerator by ax and denominator by bx to make it equivalent to theorem.
![]()
Hence, we have
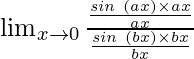
= 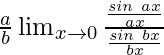
= 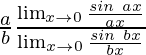
By using the theorem, we get
= ![]()
= ![]()
问题15: 
解决方案:
In ![]() , as x⇢π
, as x⇢π
Put x = π, we get
![]()
As, this limit becomes undefined
Now, let’s take π-x=p
As, x⇢π ⇒ p⇢0
![]()
= ![]()
= ![]()
By using the theorem, we get
= ![]()
= ![]()
问题16: 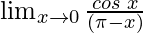
解决方案:
In ![]() , as x⇢0
, as x⇢0
Put x = 0, we get
![]()
= ![]()