问题17: 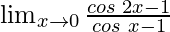
解决方案:
In![]() , as x⇢0
, as x⇢0
As we know, cos 2θ = 1-2sin2θ
Substituting the values, we get
![]()
=![]()
Put x = 0, we get
![]()
As, this limit becomes undefined
Now, let’s multiply and divide the numerator by x2 and denominator by![]() to make it equivalent to theorem.
to make it equivalent to theorem.
![]()
Hence, we have
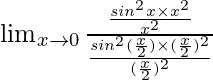
=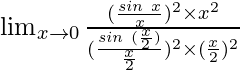
=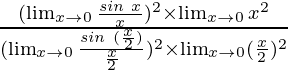
By using the theorem, we get
=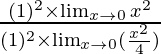
=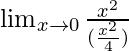
=![]()
= 4
问题18: 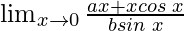
解决方案:
In![]() , as x⇢0
, as x⇢0
Put x = 0, we get
![]()
As, this limit becomes undefined
Now, let’s simplify the equation to make it equivalent to theorem.
![]()
Hence, we have
![]()
=![]()
By using the theorem, we get
=![]()
=![]()
Putting x=0, we have
=![]()
问题19: 
解决方案:
In![]() , as x⇢0
, as x⇢0
Put x = 0, we get
![]() = 0 ×1
= 0 ×1
= 0
问题20: 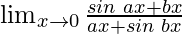
解决方案:
In![]() , as x⇢0
, as x⇢0
Put x = 0, we get
![]()
As, this limit becomes undefined
Now, let’s simplify the equation to make it equivalent to theorem.
![]()
Hence, we can write the equation as follows:
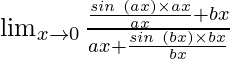
=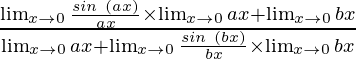
By using the theorem, we get
=![]()
=![]()
=![]()
=![]()
Putting x=0, we have
= 1
问题21: 
解决方案:
In![]() , as x⇢0
, as x⇢0
By simplification, we get
![]()
![]()
Put x = 0, we get
![]()
As, this limit becomes undefined
Now, let’s simplify the equation to make it equivalent to theorem:
![]()
By using the trigonometric identities,
cos 2θ = 1-2sin2θ
sin 2θ = 2 sinθ cosθ
Hence, we can write the equation as follows:
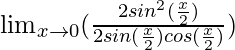
=![]()
=![]()
Putting x=0, we have
= 0
问题22: 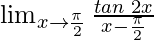
解决方案:
In![]() , as x⇢
, as x⇢![]()
Put x =![]() , we get
, we get
![]()
As, this limit becomes undefined
Now, let’s simplify the equation :
Let’s take![]()
As, x⇢![]() ⇒ p⇢0
⇒ p⇢0
Hence, we can write the equation as follows:
![]()
=![]()
=![]() (As tan (π+θ) = tan θ)
(As tan (π+θ) = tan θ)
=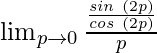
=![]()
Now, let’s multiply and divide the equation by 2 to make it equivalent to theorem
![]()
=![]()
=![]()
As p⇢0, then 2p⇢0
=![]()
Using the theorem and putting p=0, we have
= 2×1×1
= 2
问题23:查找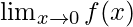 和
和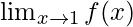 , 在哪里
, 在哪里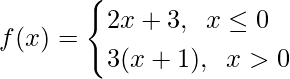
解决方案:
Let’s calculate, the limits when x⇢0
Here,
Left limit =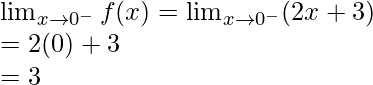
Right limit =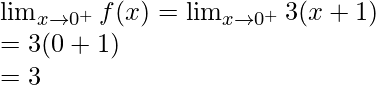
Limit value =
Hence,![]() , then limit exists
, then limit exists
Now, let’s calculate, the limits when x⇢1
Here,
Left limit =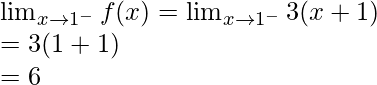
Right limit =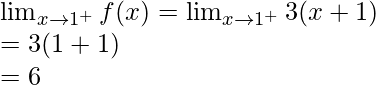
Limit value =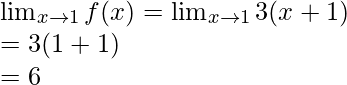
Hence,![]() , then limit exists
, then limit exists
问题24:查找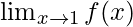 , 在哪里
, 在哪里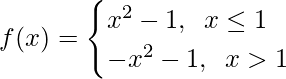
解决方案:
Let’s calculate, the limits when x⇢1
Here,
Left limit =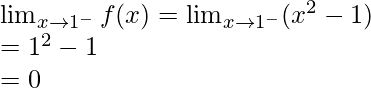
Right limit =
As,![]()
Hence, limit does not exists when x⇢1.
问题25:评估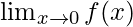 , 在哪里
, 在哪里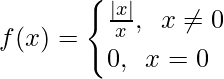
解决方案:
Let’s calculate, the limits when x⇢0
Here,
As, we know that mod function works differently.
In |x-0|, |x|=x when x>0 and |x|=-x when x<0
Left limit =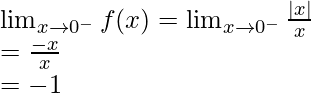
Right limit =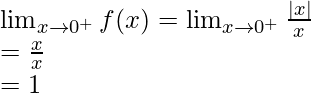
As,![]()
Hence, limit does not exists when x⇢0.
问题26:查找 , 在哪里
, 在哪里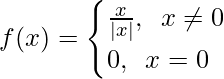
解决方案:
Let’s calculate, the limits when x⇢0
Here,
As, we know that mod function works differently.
In |x-0|, |x|=x when x>0 and |x|=-x when x<0
Left limit =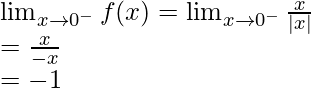
Right limit =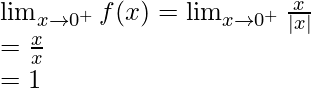
As,![]()
Hence, limit does not exists when x⇢0.
问题27:查找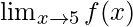 ,其中f(x)= | x | -5。
,其中f(x)= | x | -5。
解决方案:
Let’s calculate, the limits when x⇢5
Here,
As, we know that mod function works differently.
In |x-0|, |x|=x when x>0 and |x|=-x when x<0
Left limit =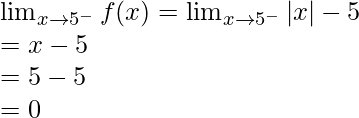
Right limit =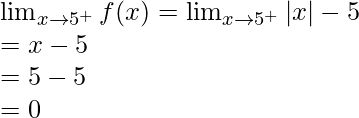
Hence,![]() , then limit exists
, then limit exists
问题28:假设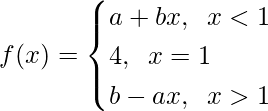 而如果
而如果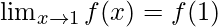 a和b的可能值是多少?
a和b的可能值是多少?
解决方案:
As, it is given![]()
Let’s calculate, the limits when x⇢1
Here,
Left limit =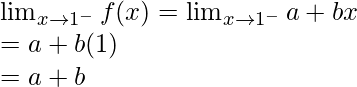
Right limit =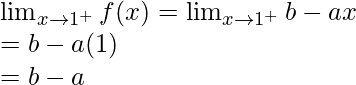
Limit value f(1) = 4
So, as limit exists then it should satisfy
![]()
Hence, a+b = 4 and b-a = 4
Solving these equation, we get
a = 0 and b = 4
问题29:让a 1 ,a 2 ,。 。 。, n是固定的实数并定义一个函数
f(x)=(xa 1 )(xa 2 )…………(x-an)。
什么是 ?对于一些≠a 1 ,a 2 ,…,an计算
?对于一些≠a 1 ,a 2 ,…,an计算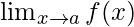 。
。
解决方案:
Here, f(x) = (x-a1) (x-a2)………… (x-an).
Then,![]()
=![]()
= (a1-a1) (a1-a2)………… (a1-an)
![]() = 0
= 0
Now, let’s calculate for![]()
![]()
=![]()
= (a-a1) (a-a2)………… (a-an)
![]() = (a-a1) (a-a2)………… (a-an)
= (a-a1) (a-a2)………… (a-an)
问题30:如果
对于a的什么值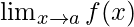 存在吗?
存在吗?
解决方案:
Here,
As, we know that mod function works differently.
In |x-0|, |x|=x when x>0 and |x|=-x when x<0
Let’s check for three cases of a:
- When a=0
Let’s calculate, the limits when x⇢0
Left limit =
Right limit =
As,![]()
Hence, limit does not exists when x⇢0.
- When a>0
Let’s take a=2, for reference
Let’s calculate, the limits when x⇢2
Left limit =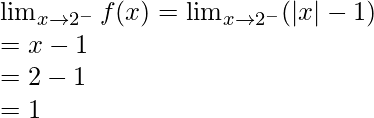
Right limit =
As,![]()
Hence, limit exists when x⇢2.
- When a<0
Let’s take a=-2, for reference
Let’s calculate, the limits when x⇢ -2
Left limit =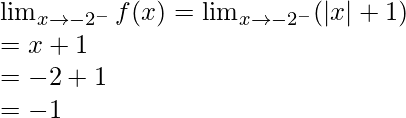
Right limit =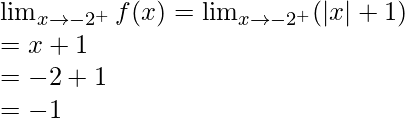
As,![]()
Hence, limit exists when x⇢ -2.
问题31:如果函数f(x)满足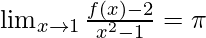 , 评估
, 评估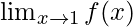
解决方案:
Here, as it is given
![]()
![]()
![]()
Put x = 1 in RHS, we get
![]()
![]()
![]()
![]() = 2
= 2
Hence proved!
问题32:如果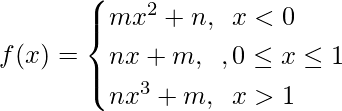 。对于整数m和n两者
。对于整数m和n两者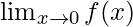 和
和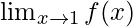 存在吗?
存在吗?
解决方案:
Let’s calculate, the limits when x⇢0
Here,
Left limit =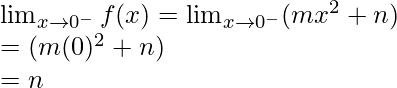
Right limit =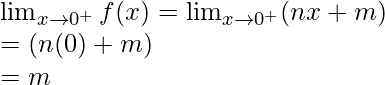
Hence,
![]() , then limit exists
, then limit exists
m = n
Now, let’s calculate, the limits when x⇢1
Here,
Left limit =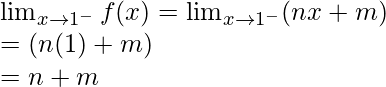
Right limit =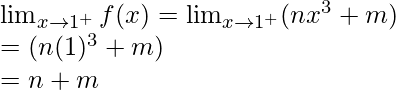
Hence,![]() , then limit exists.
, then limit exists.