问题1.将直径3 mm的铜线缠绕在长度为12 cm,直径为10 cm的圆柱体上,以覆盖圆柱体的曲面。假设铜的密度为8.88 g / cm 3 ,求出导线的长度和质量。
解决方案:
Given,
Radius of copper wire (r) = ![]() mm =
mm = ![]() cm
cm
Height of cylinder (H) = 12 cm
Radius of Cylinder (R) = ![]() = 5 cm
= 5 cm

Length of copper wire needed for one round will be circumference of cylindrical circle end = 2πR
=2π(5)
length of each round = 10π cm
Now, to completely cover the cylinder with wire no of rounds (n) of copper wire should be:
n = height of cylinder / diameter of copper wire
n = ![]()
no. of rounds = 40
Now, Total length of copper wire will be:
h = no. of rounds × length of each round
h = 40×10π
h = 400×3.14 (taking π = 3.14)
h = 1256 cm
Volume of copper wire = πr2h
=π×(![]() )2×1256
)2×1256
=π×![]() ×1256
×1256
= 88.82 cm3 (taking π = ![]() )
)
Now, as it is given that,
For 1cm3 = 8.88 g of wire
so, for 88.82 cm3 = 8.88×88.82 g
Mass of copper wire = 788.7216 g
Hence, the length and mass of the wire are1256 cm and 788.216 grams respectively.
问题2。制作一个直角三角形,其侧面为3厘米和4厘米(斜边除外)围绕其斜边旋转。找到如此形成的双锥的体积和表面积。 (选择适当的π值。)
解决方案:
After revolving the triangle about its hypotenuse, we get two cones having slant height as 3 cm and 4 cm each.
Hypotenuse of triangle (CD) = √(32 + 42) = 5 cm
l1 = 3 cm
l2 = 4 cm
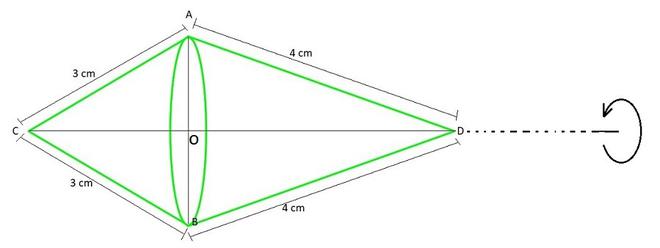
ar(△ACD) = ![]() ×AC×AD = ½×AO×CD (as AC⊥AD and AO⊥CD)
×AC×AD = ½×AO×CD (as AC⊥AD and AO⊥CD)
⇒ AC×AD = AO×CD
⇒ 4×3 = AO×5
AO = ![]() cm
cm
Hence, radius of cone base is ![]() cm
cm
Now, Volume of double cone = Volume of cone 1 + Volume of cone 2
= (![]() )πr2×OD + (
)πr2×OD + (![]() )πr2×OC
)πr2×OC
= (![]() )πr2×(OD+OC)
)πr2×(OD+OC)
= ![]() πr2×CD
πr2×CD
= ![]()
= 30.17 cm3
Now, Curve Surface area of double cone = CSA of cone 1 + CSA of cone 2
= πrl1 + πrl2
= πr(l1+l2)
= ![]() ×(3+4)
×(3+4)
= 30.17 cm2
Hence, the volume and surface area of the double cone so formed is 30.17 cm3 and 30.17 cm2 .
问题3.一个水箱,内部长150厘米×120厘米×110厘米,里面有129600厘米3的水。将多孔砖放入水中,直到水箱充满水。每块砖吸收其自身水量的十七分之一。在不溢出水的情况下可以放入多少块砖,每块砖为22.5厘米×7.5厘米×6.5厘米?
解决方案:
Given,
Length of Cistern (L) = 150 cm
Breadth of Cistern (W) = 120 cm
Height of Cistern (H) = 110 cm
Length of Brick (l) = 22.5 cm
Breadth of Brick (w) = 7.5 cm
Height of Brick (h) = 6.5 cm

Volume of Cistern = L×B×H
= 150×120×110
= 1980000 cm3
Volume of Water = 129600 cm3
Empty space left in Cistern = 1980000-129600
= 1850400 cm3
Volume of Brick = l×b×h
= 22.5×7.5×6.5
= 1096.88 cm3
Volume of n Bricks = 1096.88×n cm3
Volume absorbed by each brick = (![]() )th (volume of brick)
)th (volume of brick)
= ![]() ×1096.88 cm3
×1096.88 cm3
= 64.522 cm3
Then, Volume absorbed by n bricks = 64.522×n
Volume of brick = Empty space left in Cistern + volume absorbed by bricks
1096.88×n = 1850400 + 64.522×n
n×(1096.88-64.522) = 1850400
n = ![]()
n = 1792.40
n ≈ 1792
Hence, 1792 bricks can be put in without overflowing the water.
问题4:在给定月份的两个星期中,河谷降雨量为10厘米。如果山谷面积为7280 km 2 ,则表明总降雨量大约等于三条河流的正常水量的补充,三条河流的长度分别为1072 km,宽75 m和深3 m。
解决方案:
Length of river (l) = 1072 km
Width of river (w) = ![]() km = 0.075 km
km = 0.075 km
Depth of river (h) = ![]() = 0.003 km
= 0.003 km
Depth of rainfall = ![]() km
km
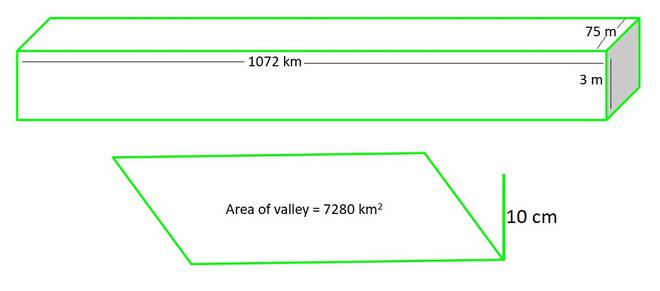
The total rainfall was approximately equivalent to the addition to the normal water of three rivers each
Which means,
(Volume of three rivers = ((Surface area of a valley)×Depth of rainfall) has to be equal.
Let’s check, for each case,
so,
Volume of three rivers = 3×(l×b×h)
= 3×(1072×0.075×0.003) km3
= 0.7236 km3 ………………………..(1)
Volume of rainfall in valley = Area of valley×depth of rainfall
= 7280×![]()
= 0.728 km3……………………………….(2)
From (1) and (2) we can see that,
Hence, proved, Total rainfall was approximately equivalent to the addition to the normal water of three rivers each.
问题5。由锡板制成的油漏斗由一个10厘米长的圆柱形部分组成,该部分附着在圆锥台上。如果总高度为22厘米,圆柱部分的直径为8厘米,漏斗顶部的直径为18厘米,请找到制作漏斗所需的锡板面积(见图13.25)。
解决方案:
Oil funnel contains two shapes = frustum + Cylinder
Given values,
Larger radius of frustum (R) = ![]() = 9 cm
= 9 cm
Smaller radius of frustum (r) = ![]() = 4 cm
= 4 cm
Height of frustum (H) = 22-10 = 12 cm
Radius of cylinder (r) = ![]() = 4 cm
= 4 cm
Height of cylinder (h) = 10 cm

Area of the tin sheet required = CSA of frustum + CSA of cylinder
CSA of frustum = π(r+R)l
= π×(9+4)×√(122 + (9-4)2) (l =√(H2 + (R-r)2))
= π×13×13
= 169π cm2
CSA of cylinder = 2πrh
= 2×π×4×10
= 80π cm2
Area of the tin sheet required = 169π + 80π
= 249π
= 782.571 cm2 (Taking π=![]() )
)
Hence, the area of the tin sheet required to make the funnel is 782.571 cm2
问题6.使用解释的符号推导第13.5节中给出的圆锥体的截头圆锥体的曲面表面积和总表面积的公式。
解决方案:
Let ADE be a cone. From the cone the frustum BCDE is cut by a plane parallel to its base. Here, r and R are the radii of the frustum ends of the cone and h be the frustum height.
Here, as BC||DE

In △ADG and △ABF
So, ΔADG ∼ ΔABF (as BC||DE)
![]()
![]() …………..(1)
…………..(1)
from (1), we get
1-(![]() ) =
) = ![]()
![]() = 1 –
= 1 – ![]()
![]() =
= ![]()
L(R-r) = Rl………………………(2) (By rearranging)
Total surface area of frustum = CSA of frustum + Area of upper circular end + Area of the lower circular end
- CSA of frustum = CSA of cone ADE – CSA of cone ABC
= πRL – πr(L-l)
= πL(R-r)+πrl
= πRl+πrl (from (2) replacing L(R-r) = Rl )
= π(R+r)l
- Area of upper circular end = πR2
- Area of the lower circular end = πr2
Total surface area of frustum = π(R+r)l + πR2 + πr2
问题7.使用解释的符号推导第13.5节中给您的圆锥台的截锥体体积的公式。
解决方案:
Let ADE be a cone. From the cone the frustum BCDE is cut by a plane parallel to its base. Here, r and R are the radii of the frustum ends of the cone and h be the frustum height.
Here, as BC||DE

In △ADG and △ABF
So, ΔADG ∼ ΔABF (as BC||DE)
![]()
![]() …………………(1)
…………………(1)
from (1), we get
1-(![]() ) =
) = ![]()
![]() = 1 –
= 1 – ![]()
![]() =
= ![]()
H(R-r) = Rh………………………(2) (By rearranging)
Total volume of frustum of the cone will be = Volume of cone ADE – Volume of cone ABC
= ![]() πR2H –
πR2H – ![]() πr2(H-h)
πr2(H-h)
= ![]() πR2H –
πR2H – ![]() πr2H +
πr2H + ![]() πr2h
πr2h
= ![]() π(H(R2-r2)+r2h)
π(H(R2-r2)+r2h)
= ![]() π(H(R-r)(R+r)+r2h) (Replacing (R2-r2) = (R-r)(R+r))
π(H(R-r)(R+r)+r2h) (Replacing (R2-r2) = (R-r)(R+r))
= ![]() π(Rh(R+r)+r2h) (from (2) replacing H(R-r) = Rh )
π(Rh(R+r)+r2h) (from (2) replacing H(R-r) = Rh )
= ![]() π(R2h+Rrh+r2h)
π(R2h+Rrh+r2h)
= ![]() πh(R2+Rr+r2) (Taking h common)
πh(R2+Rr+r2) (Taking h common)
Hence, Total volume of frustum of the cone will be = ![]() πh(R2+Rr+r2)
πh(R2+Rr+r2)