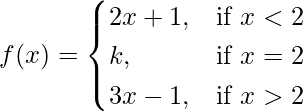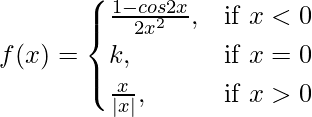第 12 类 RD Sharma 解决方案 - 第 9 章连续性 - 练习 9.1 |设置 3

问题 31. 如果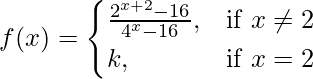$f(x)=\begin{cases}\frac{2^{x+2}-16}{4^x-16},& \text{if }x\neq2 \\k,& \text{if }x=2\end{cases}$在 x = 2 处连续，求 k。

解决方案：

Given that,

$f(x)=\begin{cases}\frac{2^{x+2}-16}{4^x-16},& \text{if }x\neq2 \\k,& \text{if }x=2\end{cases}$

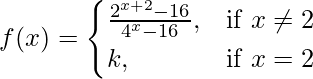
Also, f(x) is continuous at x = 2

So, LHL = RHL = f(2)        …..(i)

Now,

f(2) = k  ……(ii)

Let us consider LHL,

$\lim_{x\to2^-}f(x) =\lim_{h\to0}f(2-h)$

$=\lim_{h\to0}\frac{2^{(2-h)+2}-16}{4^{(2-h)}-16}$

$=\lim_{h\to0}\frac{2^{4-h}-16}{4^{(2-h)}-16}$

$=\lim_{h\to0}\frac{2^4.2^{-h}-16}{4^2.4^{-h}-16}$

$=\lim_{h\to0}\frac{16.2^{-h}-16}{16.4^{-h}-16}$

$=\lim_{h\to0}\frac{16(2^{-h}-1)}{16(4^{-h}-1)}$

$=\lim_{h\to0}\frac{2^{-h}-1}{(2^{-h})^2-1^2}$

$=\lim_{h\to0}\frac{2^{-h}-1}{(2^{-h}-1)(2^{-h}+1)}=1/2$    ……(iii)

Using eq(i), (ii) and (iii), we get

k = 1/2

问题 32. 如果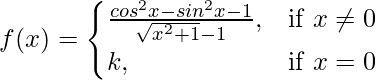$f(x)=\begin{cases}\frac{cos^2x-sin^2x-1}{\sqrt{x^2+1}-1},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$在 x = 0 处连续，求 k。

解决方案：

Given that, 

$f(x)=\begin{cases}\frac{cos^2x-sin^2x-1}{\sqrt{x^2+1}-1},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$

Also, f(x) is continuous at x = 2

So, LHL = RHL

Now,

$\lim_{x\to0}f(x)=f(0)$

⇒ $\lim_{x\to0}\frac{cos^2x-sin^2x-1}{\sqrt{x^2+1}-1}=k$

⇒ $\lim_{x\to0}\frac{1-sin^2x-sin^2x-1}{\sqrt{x^2+1}-1}=k$

⇒ $\lim_{x\to0}\frac{-2sin^2x}{\sqrt{x^2+1}-1}=k$

⇒ $\lim_{x\to0}\frac{-2(sin^2x)(\sqrt{x^2+1}+1)}{(\sqrt{x^2+1}-1)(\sqrt{x^2+1}+1)}=k$

⇒ $\lim_{x\to0}\frac{-2(sin^2x)(\sqrt{x^2+1}+1)}{x^2}=k$

⇒ $-2\lim_{x\to0}\frac{(sin^2x)(\sqrt{x^2+1}+1)}{x^2}=k$

⇒ $-2\lim_{x\to0}(\frac{sinx}{x})^2\lim_{x\to0}(\sqrt{x^2+1}+1)=k$

⇒ -2 × 1 × (1 + 1) = k

⇒ k = -4

问题 33. 通过连续性扩展以下定义 f(x) = 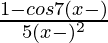$\frac{1-cos7(x-π)}{5(x-π)^2}$在点 x = π。

解决方案：

Given that, 

$\frac{1-cos7(x-π)}{5(x-π)^2}$

As we know that a f(x) is continuous at x = π if,

LHL = RHL = f(π)  ……(i)

Let us consider LHL,

$\lim_{x\toπ^-}f(x) =\lim_{h\to0}f(π-h)$

$=\lim_{h\to0}\frac{1-cos7(π-h-π)}{5((π-h)-π)^2}$

$=\lim_{h\to0}\frac{2sin^2(7/2)h}{5h^2}$

$=\lim_{h\to0}(2/5)(\frac{sin(7/2)h}{(7/2)h})^2×(7/2)^2$

= (2/5) × (49/4) = 49/10

 Thus, from eq(i) we get,

f(π) = 49/10

Hence, f(x) is continuous at x = π

问题 34. 如果 f(x) = 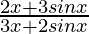$\frac{2x+3sinx}{3x+2sinx}$ , x ≠ 0 在 x = 0 处连续，则求 f(0)。

解决方案：

Given that, 

f(x) = $\frac{2x+3sinx}{3x+2sinx}$

Also, f(x) is continuous at x = 0

So, LHL = RHL = f(0)     ……(i)

Let us consider LHL,

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}\frac{2(-h)+3sin(-h)}{3(-h)+2sin(-h)}$

$=\lim_{h\to0}\frac{-2h-3sinh}{-3h-2sinh}$

$=\lim_{h\to0}\frac{\frac{2h+3sinh}{h}}{\frac{3h+2sinh}{h}}$

$=\lim_{h\to0}\frac{2+3\frac{sinh}{h}}{3+2\frac{sinh}{h}}=\frac{2+3}{3+2}=1$

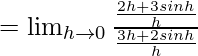
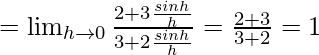
From eq(i) we get,

f(0) = 1

问题 35. 求 k 的值$f(x)=\begin{cases}\frac{1-cos4x}{8x^2} ,& \text{when }x\neq0 \\k,& \text{when }x=0\end{cases}$在 x = 0 处是连续的

解决方案：

Given that, 

$f(x)=\begin{cases}\frac{1-cos4x}{8x^2} ,& \text{when }x\neq0 \\k,& \text{when }x=0\end{cases}$

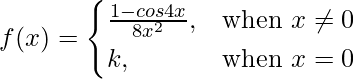
Also, f(x) is continuous at x = 0

LHL = RHL = f(0)     …..(i)

f(0) = k

Let us consider LHL,

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}\frac{1-cos4(-h)}{8(-h)^2}$

$=\lim_{h\to0}\frac{1-cos4h}{8h^2}$

$=\lim_{h\to0}\frac{2sin^22h}{8h^2}$

$=\lim_{h\to0}(\frac{sin2h}{2h})^2=1$

Thus, from eq(i) we get,

k = 1

问题 36. 在以下每一项中，找到常数 k 的值，使得给定函数在指定点是连续的：

（一世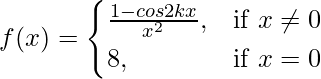） $f(x)=\begin{cases}\frac{1-cos2kx}{x^2},& \text{if }x\neq0 \\8,& \text{if }x=0\end{cases}$在 x = 0

解决方案：

Given that, 

$f(x)=\begin{cases}\frac{1-cos2kx}{x^2},& \text{if }x\neq0 \\8,& \text{if }x=0\end{cases}$

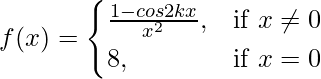
Also, f(x) is continuous at x = 0

$\lim_{x\to0}f(x) =f(0)$

⇒ $\lim_{x\to0}\frac{1-cos2kx}{x^2}=8$

⇒ $\lim_{x\to0}\frac{2k^2sin^2kx}{k^2x^2}=8$

⇒ $2k^2\lim_{x\to0}(\frac{sinkx}{kx})^2=8$

⇒ 2k² × 1 = 8

⇒ k² = 4

⇒ k = ±2

(二) 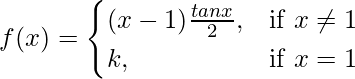$f(x)=\begin{cases}(x-1)\frac{tanπx}{2},& \text{if }x\neq1 \\k,& \text{if }x=1\end{cases}$在 x = 1

解决方案：

Given that, 

$f(x)=\begin{cases}(x-1)\frac{tanπx}{2},& \text{if }x\neq1 \\k,& \text{if }x=1\end{cases}$

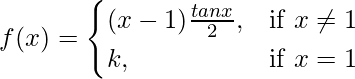
Also, f(x) is continuous at x = 1

$\lim_{x\to1}f(x) =f(1)$

⇒ $\lim_{x\to1}(x-1)tan(πx/2)=k$

Now, on putting x – 1 = y, we get

$\lim_{y\to0}ytan\frac{π(y+1)}{2}=k$

⇒ $\lim_{y\to0}ytan(\frac{πy}{2}+π/2)=k$

⇒ $\lim_{y\to0}ytan(\frac{π}{2}+\frac{πy}{2})=k$

⇒ $-\lim_{y\to0}ycot(\frac{π}{2})=k$

⇒ $\frac{-2}{π}\lim_{y\to0}\frac{\frac{πy}{2}cos(\frac{πy}{2})}{sin\frac{πy}{2}}=k$

⇒ $\frac{-2}{π}\frac{\lim_{y\to0}cos(\frac{πy}{2})}{\lim_{y\to0}(\frac{sin(\frac{πy}{2})}{\frac{πy}{2}})}=k$

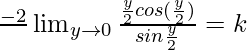
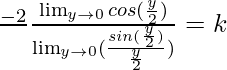
⇒ (-2/π) × (1/1) = k

⇒ k = (-2/π)

㈢ 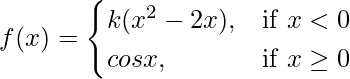$f(x)=\begin{cases}k(x^2-2x),& \text{if }x<0 \\cosx,& \text{if }x\geq0\end{cases}$在 x = 0

解决方案：

Given that, 

$f(x)=\begin{cases}k(x^2-2x),& \text{if }x<0 \\cosx,& \text{if }x\geq0\end{cases}$

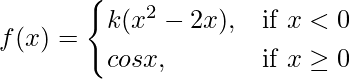
Also, f(x) is continuous at x = 0

Let us consider LHL, at x = 0

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}f(-h)$

$=\lim_{h\to0}k(h^2+2h)=0$

Let us consider RHL at x = 0

$\lim_{x\to0^+}f(x) =\lim_{h\to0}f(0+h)$

$=\lim_{h\to0}f(h)$

$=\lim_{h\to0}cosh=1$

$\lim_{x\to0^-}f(x)≠\lim_{x\to0^+}f(x)$

Hence, no value of k exists for which function is continuous at x = 0.

(四) 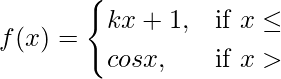$f(x)=\begin{cases}kx+1,& \text{if }x\leqπ \\cosx,& \text{if }x>π\end{cases}$在 x = π

解决方案：

Given that, 

$f(x)=\begin{cases}kx+1,& \text{if }x\leqπ \\cosx,& \text{if }x>π\end{cases}$

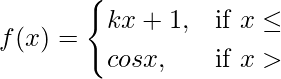
Also, f(x) is continuous at x = π

Let us consider LHL 

$\lim_{x\toπ^-}f(x) =\lim_{h\to0}f(π-h)$

$=\lim_{h\to0}k(π-h)+1=kπ+1$

Let us consider RHL 

$\lim_{x\toπ^+}f(x) =\lim_{h\to0}f(π+h)$

$=\lim_{h\to0}cos(π+h)$

cosπ = -1

As we know that f(x) is continuous at x = π, so

$\lim_{x\toπ^-}f(x)=\lim_{x\toπ^+}f(x)$

⇒ kπ + 1 = -1

⇒ k = (-2/π)

(五) 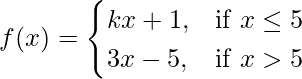$f(x)=\begin{cases}kx+1,& \text{if }x\leq5 \\3x-5,& \text{if }x>5\end{cases}$在 x = 5

解决方案：

Given that, 

$f(x)=\begin{cases}kx+1,& \text{if }x\leq5 \\3x-5,& \text{if }x>5\end{cases}$

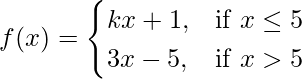
Also, f(x) is continuous at x = 5

Let us consider LHL 

$\lim_{x\to5^-}f(x)=\lim_{h\to0}f(5-h)$

$=\lim_{h\to0}k(5-h)+1$

= 5k + 1

Let us consider RHL 

$\lim_{x\to5^+}f(x)=\lim_{h\to0}f(5+h)$

$=\lim_{h\to0}3(5+h)-5$

= 10

As we know that f(x) is continuous at x = 5, so

$\lim_{x\to5^-}f(x)=\lim_{x\to5^+}f(x)$

⇒ 5k + 1 = 10

⇒ k = 9/5

(六) 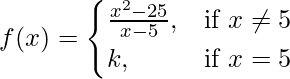$f(x)=\begin{cases}\frac{x^2-25}{x-5},& \text{if }x\neq5 \\k,& \text{if }x=5\end{cases}$在 x = 5

解决方案：

Given that, 

$f(x)=\begin{cases}\frac{x^2-25}{x-5},& \text{if }x\neq5 \\k,& \text{if }x=5\end{cases}$

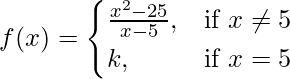
Also, f(x) is continuous at x = 5

So, 

f(x) = (x² – 25)/(x – 5), if x ≠ 5 & f(x) = k, if x = 5

⇒ f(x)= {(x – 5)(x+5)/(x-5)}, if x ≠ 5 & f(x) = k, if x = 5

⇒ f(x)= (x + 5), if x ≠ 5 & f(x) = k, if x = 5

As we know that f(x) is continuous at x = 5, so

$\lim_{x\to5}f(x)=f(5)$

⇒ $\lim_{x\to5}(x+5)=k$

⇒ k = 5 + 5 = 10

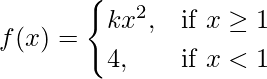(七) $f(x)=\begin{cases}kx^2,& \text{if }x\geq1 \\4,& \text{if }x<1\end{cases}$在 x = 1

解决方案：

Given that, 

$f(x)=\begin{cases}kx^2,& \text{if }x\geq1 \\4,& \text{if }x<1\end{cases}$

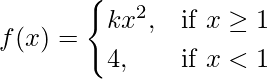
Also, f(x) is continuous at x = 1

Let us consider LHL 

$\lim_{x\to1^-}f(x)=\lim_{h\to0}f(1-h)$

$=\lim_{h\to0}4=4$

Let us consider RHL 

$\lim_{x\to1^+}f(x)=\lim_{h\to0}f(1+h)$

$=\lim_{h\to0}k(1+h)^2$

= k

As we know that f(x) is continuous at x = 1, so

$\lim_{x\to1^-}f(x)=\lim_{x\to1^+}f(x)$

⇒ k = 4

(八) $f(x)=\begin{cases}k(x^2+2),& \text{if }x\leq0 \\3x+1,& \text{if }x>0\end{cases}$在 x = 0

解决方案：

Given that, 

$f(x)=\begin{cases}k(x^2+2),& \text{if }x\leq0 \\3x+1,& \text{if }x>0\end{cases}$

Also, f(x) is continuous at x = 0

Let us consider LHL 

$\lim_{x\to0^-}f(x)=\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}k((-h)^2+2)$

= 2k

Let us consider RHL 

$\lim_{x\to0^+}f(x)=\lim_{h\to0}f(0+h)$

$=\lim_{h\to0}3h+1$

= 1

As we know that f(x) is continuous at x = 0, so

$\lim_{x\to0^-}f(x)=\lim_{x\to0^+}f(x)$

⇒ 2k = 1

⇒ k = 1/2

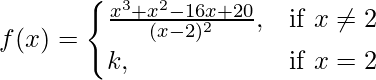(九) $f(x)=\begin{cases}\frac{x^3+x^2-16x+20}{(x-2)^2},& \text{if }x\neq2 \\k,& \text{if }x=2\end{cases}$在 x = 2

解决方案：

Given that, 

$f(x)=\begin{cases}\frac{x^3+x^2-16x+20}{(x-2)^2},& \text{if }x\neq2 \\k,& \text{if }x=2\end{cases}$

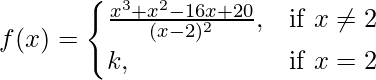
Also, f(x) is continuous at x = 2

f(x)= $\frac{x^3+x^2-16x+20}{(x-2)^2}$, if x ≠ 2 & f(x) = k, if x = 2

⇒ f(x)= $\frac{x^3+x^2-16x+20}{x^2-4x+4}$ , if x ≠ 2 & f(x) = k, if x = 2

⇒ f(x)= $\frac{(x+5)(x^2-4x+4)}{x^2-4x+4}$ , if x ≠ 2 & f(x) = k, if x = 2

⇒ f(x)= (x + 5), if x ≠ 2 & f(x) = k, if x = 2

As we know that f(x) is continuous at x = 2, so

$\lim_{x\to2}f(x)=f(2)$

⇒ $\lim_{x\to2}(x+5)=f(2)$

⇒ k = 2 + 5 = 7

问题 37. 求 a 和 b 的值，使得函数f 由下式给出

$f(x)=\begin{cases}1,& \text{if }x\leq3 \\ax+b,& \text{if }3<x<5\\7, &\text{if }x\geq5\end{cases}$在 x = 3 和 x = 5 处是连续的。

解决方案：

Given that, 

$f(x)=\begin{cases}1,& \text{if }x\leq3 \\ax+b,& \text{if }3<x<5\\7, &\text{if }x\geq5\end{cases}$

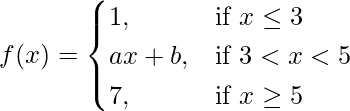
Let us consider LHL at x = 3,

$\lim_{x\to3^-}f(x)=\lim_{h\to0}f(3-h)$

$=\lim_{h\to0}(1)$

= 1

Let us consider RHL at x = 3,

$\lim_{x\to3^+}f(x)=\lim_{h\to0}f(3+h)$

$=\lim_{h\to0}a(3+h)+b$

= 3a + b

Let us consider LHL at x = 5,

$\lim_{x\to5^-}f(x)=\lim_{h\to0}f(5-h)$

$=\lim_{h\to0}(a(5-h)+b)$

= 5a + b

Let us consider RHL at x = 5,

$\lim_{x\to5^+}f(x)=\lim_{h\to0}f(5+h)$

$=\lim_{h\to0}7$

= 7

It is given that f(x) is continuous at x = 3 and x = 5, then

$\lim_{x\to3^-}f(x)=\lim_{x\to3^+}f(x)$ and $\lim_{x\to5^-}f(x)=\lim_{x\to5^+}f(x)$

⇒ 1 = 3a + b …..(i) 

and 5a + b = 7 …….(ii)

On solving eq(i) and (ii), we get

a = 3 and b = -8

问题 38. 如果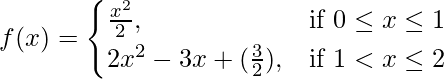$f(x)=\begin{cases}\frac{x^2}{2},& \text{if }0\leq x \leq 1 \\2x^2-3x+(\frac{3}{2}),& \text{if }1<x\leq2\end{cases}$ .证明 f 在 x = 1 处是连续的。

解决方案：

Given that, 

$f(x)=\begin{cases}\frac{x^2}{2},& \text{if }0\leq x \leq 1 \\2x^2-3x+(\frac{3}{2}),& \text{if }1<x\leq2\end{cases}$

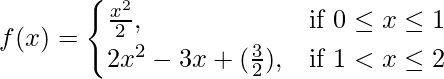
So, 

Let us consider LHL at x = 1,

$\lim_{x\to1^-}f(x)=\lim_{h\to0}f(1-h)$

$=\lim_{h\to0}\frac{(1-h)^2}{2}$

= 1/2

Let us consider RHL at x = 1,

$\lim_{x\to1^+}f(x)=\lim_{h\to0}f(1+h)$

$=\lim_{h\to0}[2(1+h)^2-3(1+h)+3/2]$

= 2 – 3 + 3/2 = 1/2

Also,

f(1) = (1)²/2 = 1/2

$\lim_{x\to1^-}f(x)=\lim_{x\to1^+}f(x)=f(1)$

LHL = RHL = f(1)

Hence, the f(x) is continuous at x = 1

问题 39. 讨论 f(x) 在指定点的连续性：

(i) f(x) = |x| + |x - 1|在 x = 0, 1。

解决方案：

Given that, 

f(x) = |x| + |x – 1|

So, here we check the continuity of the given f(x) at x = 0,

Let us consider LHL at x = 0,

$\lim_{x\to0^-}f(x)=\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}[|0-h|+|0-h-1|]=1$

Let us consider RHL at x = 0,

$\lim_{x\to0^+}f(x)=\lim_{h\to0}f(0+h)$

$=\lim_{h\to0}[|0+h|+|0+h-1|]=1$

Also,

f(0) = |0| + |0 – 1| = 0 + 1 = 1

LHL = RHL = f(0)

Now, we check the continuity of the given f(x) at x = 1,

Let us consider LHL at x = 1,

$\lim_{x\to1^-}f(x)=\lim_{h\to0}f(1-h)$

$=\lim_{h\to0}f(|1-h|+|1-h-1|)=1+0$

= 1

Let us consider RHL at x = 1

$\lim_{x\to1^+}f(x)=\lim_{h\to0}f(1+h)$

$=\lim_{h\to0}f(|1+h|+|1+h-1|)=1+0$

= 1

Also,

f(1) = |1| + |1 – 1| = 1 + 0 = 1

LHL = RHL = f(1)

Hence, f(x) is continuous at x = 0, 1.

(ii) f(x) = |x – 1| + |x + 1|在 x = -1, 1。

解决方案：

Given that, 

f(x) = |x – 1| + |x + 1| at x = -1, 1.

So, here we check the continuity of the given f(x) at x = -1,

Let us consider LHL at x = -1,

$\lim_{x\to-1^-}f(x)=\lim_{h\to0}f(-1-h)$

$=\lim_{h\to0}[|-1-h-1|+|-1-h+1|]=2+0=2$

Let us consider RHL at x = -1,

$\lim_{x\to-1^+}f(x)=\lim_{h\to0}f(-1+h)$

$=\lim_{h\to0}[|-1+h-1|+|-1+h+1|]=2+0=2$

Also,

f(-1) = |-1 – 1| + |-1 + 1| = |-2| = 2

LHL = RHL = f(-1)

Now, we check the continuity of the given f(x) at x = 1,

Let us consider LHL at x = 1,

$\lim_{x\to1^-}f(x)=\lim_{h\to0}f(1-h)$

$=\lim_{h\to0}f(|1-h-1|+|1-h+1|)=0+2$

= 2

$\lim_{x\to1^+}f(x)=\lim_{h\to0}f(1+h)$

$=\lim_{h\to0}f(|1+h-1|+|1+h+1|)=0+2$

= 2

Also,

f(1) = |1 + 1| + |1 – 1| = 2

LHL = RHL = f(1)

Hence, f(x) is continuous at x = -1, 1.

问题 40. 证明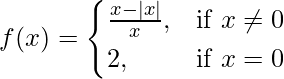$f(x)=\begin{cases}\frac{x-|x|}{x},& \text{if }x\neq0 \\2,& \text{if }x=0\end{cases}$在 x = 0 处不连续。

解决方案：

Prove that 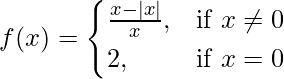$f(x)=\begin{cases}\frac{x-|x|}{x},& \text{if }x\neq0 \\2,& \text{if }x=0\end{cases}$ is discontinuous at x = 0.

Proof:

Let us consider LHL at x = 0,

$\lim_{x\to0^-}f(x)=\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}f(-h)$

$=\lim_{h\to0}2=2$

Let us consider RHL at x = 0,

$\lim_{x\to0^+}f(x)=\lim_{h\to0}f(0+h)$

$=\lim_{h\to0}f(h)$

$=\lim_{h\to0}0=0$

LHL ≠ RHL

Hence, f(x) is discontinuous at x = 0.

问题 41. 如果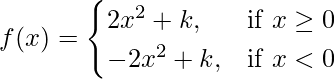$f(x)=\begin{cases}2x^2+k,& \text{if }x\geq0 \\-2x^2+k,& \text{if }x<0\end{cases}$那么 k 的值应该是多少，这样 f(x) 在 x = 0 处是连续的。

解决方案：

Given that,

$f(x)=\begin{cases}2x^2+k,& \text{if }x\geq0 \\-2x^2+k,& \text{if }x<0\end{cases}$

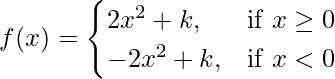
Let us consider LHL at x = 0,

$\lim_{x\to0^-}f(x)=\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}f(-h)$

$=\lim_{h\to0}-2(-h)^2+k$

= k

Let us consider RHL at x = 0,

$\lim_{x\to0^+}f(x)=\lim_{h\to0}f(0+h)$

$=\lim_{h\to0}f(h)$

$=\lim_{h\to0}f(2h^2+k)$

= k

It is given that f(x) is continuous at x = 0.

LHL = RHL = f(0)

⇒ $\lim_{x\to0^-}f(x)=\lim_{x\to0^+}f(x)=k$

k can be any real number.

问题 42.函数的 λ 值是多少

$f(x)=\begin{cases}λ(x^2-2x),& \text{if }x\leq0 \\4x+1,& \text{if }x>0\end{cases}$在 x = 0 处连续？ x = ±1 处的连续性如何？

解决方案：

Given that,

$f(x)=\begin{cases}λ(x^2-2x),& \text{if }x\leq0 \\4x+1,& \text{if }x>0\end{cases}$

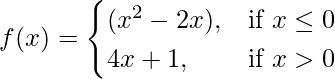
Check for x = 0, 

Hence, there is no value of λ for which f(x) is continuous at x = 0.

Now for x = 1,

f(1) = 4x + 1 = 4 × 1 + 1 = 5

Hence, for any values of λ, f is continuous at x = 1.

Now for x = -1, 

f(-1) = λ(1 + 2)= 3λ

$=\lim_{x\to-1}λ(1+2)=3λ$

 $=\lim_{x\to-1}f(x)=f(-1)$

Hence, for any values of λ, f is continuous at x=-1.

问题 43. 对于什么 k 值，以下函数在 x = 2 处连续？

$f(x)=\begin{cases}2x+1,& \text{if }x<2 \\k,& \text{if }x=2\\3x-1,& \text{if }x>2\end{cases}$

解决方案：

Given that,

$f(x)=\begin{cases}2x+1,& \text{if }x<2 \\k,& \text{if }x=2\\3x-1,& \text{if }x>2\end{cases}$

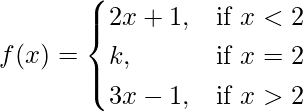
We have,

Let us consider LHL at x = 2,

$=\lim_{x\to2^-}f(x)=\lim_{h\to0}f(2-h)$

$=\lim_{h\to0}(2(2-h)+1)$

= 5

Let us consider RHL at x = 2,

$\lim_{x\to2^+}f(x)=\lim_{h\to0}f(2+h)$

$=\lim_{h\to0}3(2+h)-1$

= 5

Also,

f(2) = k

It is given that f(x) is continuous at x = 2.

LHL = RHL = f(2)

⇒ 5 = 5 = k

Hence, for k = 5, f(x) is continuous at x = 2.

问题 44. 让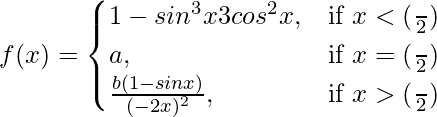$f(x)=\begin{cases}1-sin^3x3cos^2x,& \text{if }x<(\frac{π}{2}) \\a,& \text{if }x=(\frac{π}{2})\\\frac{b(1-sinx)}{(π-2x)^2},& \text{if }x>(\frac{π}{2})\end{cases}$如果 f(x) 在 x = (π/2) 处连续，求 a 和 b。

解决方案：

Given that,

$f(x)=\begin{cases}1-sin^3x3cos^2x,& \text{if }x<(\frac{π}{2}) \\a,& \text{if }x=(\frac{π}{2})\\\frac{b(1-sinx)}{(π-2x)^2},& \text{if }x>(\frac{π}{2})\end{cases}$

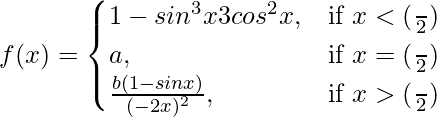
Let us consider LHL at x = π/2

$=\lim_{x\to(\frac{π}{2})^-}f(x)=\lim_{h\to0}f(\frac{π}{2}-h)$

$=\lim_{h\to0}\frac{1-sin^3(\frac{π}{2}-h)}{3cos^2(\frac{π}{2}-h)}$

$=\lim_{h\to0}\frac{1-cos^3h}{3sin^2h}$

$=\frac{1}{3}\lim_{h\to0}(\frac{(1-cosh)(1+cos^2h+cosh)}{(1-cosh)(1+cosh)})$

$=\frac{1}{3}\lim_{h\to0}(\frac{(1+cos^2h+cosh)}{(1+cosh)})$

$=\frac{1}{3}(\frac{1+1+1}{1+1})$

= 1/2

Let us consider RHL at x = π/2

$=\lim_{x\to(\frac{π}{2})^+}f(x)=\lim_{h\to0}f(\frac{π}{2}+h)$

$=\lim_{h\to0}(\frac{b[1-sin(\frac{π}{2}+h)]}{[π-2(\frac{π}{2}+h)]^2})$

$=\lim_{h\to0}(\frac{b(1-cosh)}{[-2h]^2})$

$=\lim_{h\to0}(\frac{2bsin^2(\frac{h}{2})}{4h^2})$

$=\lim_{h\to0}(\frac{2bsin^2(\frac{h}{2})}{\frac{16h^2}{4}})$

$=(\frac{b}{8})\lim_{h\to0}(\frac{sin(\frac{h}{2})}{\frac{h}{2}})^2$

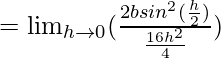
= b/8 × 1

= b/8

Also,

f(π/2) = a

It is given that f(x) is continuous at x = π/2.

LHL = RHL = f(π/2)

So, 

⇒ 1/2 = b/8 = a

⇒ a = 1/2 and b = 4

问题 45. 如果下面定义的函数 f(x) 在 x = 0 处是连续的，求 k 的值，

$f(x)=\begin{cases}\frac{1-cos2x}{2x^2},& \text{if }x<0 \\k,& \text{if }x=0\\\frac{x}{|x|},& \text{if }x>0\end{cases}$

解决方案：

Given that,

$f(x)=\begin{cases}\frac{1-cos2x}{2x^2},& \text{if }x<0 \\k,& \text{if }x=0\\\frac{x}{|x|},& \text{if }x>0\end{cases}$

Let us consider LHL at x = 0,

$=\lim_{x\to0^-}f(x)=\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}(\frac{1-cos2(-h)}{2(-h)^2})$

$=\lim_{h\to0}(\frac{1-cos2h}{2h^2})$

$=\frac{1}{2}\lim_{h\to0}(\frac{2sin^2h}{h^2})$

$=\frac{2}{2}\lim_{h\to0}(\frac{sin^2h}{h^2})$

$=\frac{2}{2}\lim_{h\to0}(\frac{sinh}{h})^2$

= 1 × 1

Let us consider RHL at x = 0,

$\lim_{x\to0^+}f(x)=\lim_{h\to0}f(0+h)$

$=\lim_{h\to0}f(h)$

$=\lim_{h\to0}1=1$

Also,

f(0) = k

It is given that f(x) is continuous at x = 0,

LHL = RHL = f(0)

So, 

⇒ 1 = 1 = k

Hence, the required value of k is 1.

问题 46. 找出 'a' 和 'b' 之间的关系，使得函数'f' 定义为

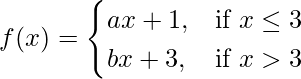$f(x)=\begin{cases}ax+1,& \text{if }x\leq3 \\bx+3,& \text{if }x>3\\\end{cases}$在 x = 3 处是连续的。

解决方案：

Given that,

$f(x)=\begin{cases}ax+1,& \text{if }x\leq3 \\bx+3,& \text{if }x>3\\\end{cases}$

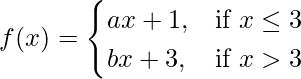
Let us consider LHL at x = 3,

$\lim_{x\to3^-}f(x)=\lim_{h\to0}f(3-h)$

$=\lim_{h\to0}a(3-h)+1$

= 3a + 1

Let us consider RHL at x = 3,

$\lim_{x\to3^+}f(x)=\lim_{h\to0}f(3+h)$

$=\lim_{h\to0}b(3+h)+3$

= 3b + 3

It is given that f(x) is continuous at x = 3,

LHL = RHL = f(3)

So, 

⇒ 3a + 1 = 3b + 3

⇒ 3a – 3b = 2

Hence, the required relationship between a and b is 3a – 3b = 2.