第 12 类 RD Sharma 解 – 第 20 章定积分 – 练习 20.2 |设置 2
计算以下定积分:
问题 21。 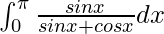
解决方案:
We have,
I = ![]()
Let sin x = A (sin x + cos x) + B![]()
=> sin x = A (sin x + cos x) + B (cos x – sin x)
=> sin x = sin x (A – B) + cos x (A + B)
On comparing both sides, we get
A – B = 1 and A + B = 0
On solving, we get A = 1/2 and B = –1/2.
Therefore, the expression becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 22。 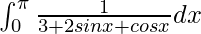
解决方案:
We have,
I = ![]()
On putting cos x = 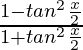 and sin x =
and sin x = ![]() , we get,
, we get,
I = 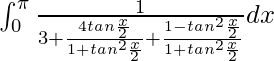
I = 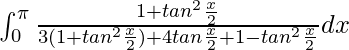
I = 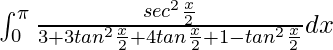
I = 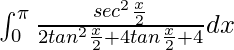
Let tan x/2 = t. So, we have
=> 1/2 sec2 x/2 dx = dt
=> sec2 x/2 dx = 2 dt
Now, the lower limit is, x = 0
=> t = tan x/2
=> t = tan 0/2
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π
=> t = tan x/2
=> t = tan π/2
=> t = ∞
So, the equation becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 23。 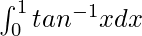
解决方案:
We have,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 24。 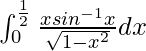
解决方案:
We have,
I = 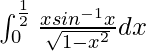
Let sin–1 x = t. So, we have
=> ![]() = dt
= dt
Now, the lower limit is, x = 0
=> t = sin–1 x
=> t = sin–1 0
=> t = 0
Also, the upper limit is, x = 1/2
=> t = sin–1 x
=> t = sin–1 1/2
=> t = π/6
So, the equation becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of 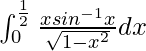 is
is ![]() .
.
问题 25。 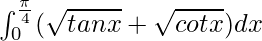
解决方案:
We have,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = 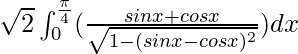
Let sinx – cosx = t. So, we have
=> (cos x + sin x) dx = dt
Now, the lower limit is, x = 0
=> t = sinx – cosx
=> t = sin 0 – cos 0
=> t = 0 – 1
=> t = –1
Also, the upper limit is, x = π/4
=> t = sinx – cosx
=> t = sin π/4 – cos π/4
=> t = sin π/4 – sin π/4
=> t = 0
So, the equation becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 26。 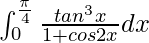
解决方案:
We have,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Let tan x = t. So, we have
=> sec2 x dx = dt
Now, the lower limit is, x = 0
=> t = tan x
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π/4
=> t = tan x
=> t = tan π/4
=> t = 1
So, the equation becomes,
I = ![]()
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{t^4}{4}\right]_{0}^{1}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_70.jpg)
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 27。 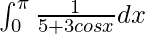
解决方案:
We have,
I = ![]()
On putting cos x = 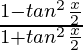 , we get
, we get
I = 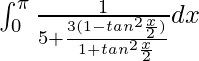
I = 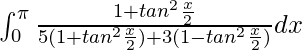
I = 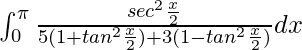
Let tan x/2 = t. So, we have
=> 1/2 sec2 x/2 dx = dt
=> sec2 x/2 dx = 2 dt
Now, the lower limit is, x = 0
=> t = tan x/2
=> t = tan 0/2
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π
=> t = tan x/2
=> t = tan π/2
=> t = ∞
So, the equation becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 28。 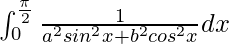
解决方案:
We have,
I = ![]()
I = 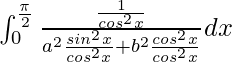
I = ![]()
I = 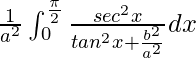
Let tan x = t. So, we have
=> sec2 x dx = dt
Now, the lower limit is, x = 0
=> t = tan x
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = tan x
=> t = tan π/2
=> t = ∞
So, the equation becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 29。 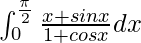
解决方案:
We have,
I = ![]()
I = ![]()
I = ![]()
I = ![Rendered by QuickLaTeX.com \left[xtan\frac{x}{2}-\int_{0}^{\frac{\pi}{2}}tan\frac{x}{2}dx+\int_{0}^{\frac{\pi}{2}}tan\frac{x}{2}dx\right]^{\frac{\pi}{2}}_0](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_108.jpg)
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 30。 
解决方案:
We have,
I = ![]()
Let tan–1 x = t. So, we have
=> ![]() = dt
= dt
Now, the lower limit is, x = 0
=> t = tan–1 x
=> t = tan–1 0
=> t = 0
Also, the upper limit is, x = 1
=> t = tan–1 x
=> t = tan–1 1
=> t = π/4
So, the equation becomes,
I = ![]()
I = ![Rendered by QuickLaTeX.com \left[\frac{t^2}{2}\right]_{0}^{\frac{\pi}{4}}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_118.jpg)
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 31。 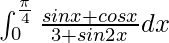
解决方案:
We have,
I = ![]()
I = ![]()
I = ![]()
I = ![Rendered by QuickLaTeX.com \left[\frac{1}{4}log|\frac{2+sinx-cosx}{2-sinx+cosx}|\right]_{0}^{\frac{\pi}{4}}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_127.jpg)
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 32。 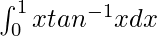
解决方案:
We have,
I = ![]()
On using integration by parts, we get
I = ![]()
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{x^2}{1+x^2}dx](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_139.jpg)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{1+x^2-1}{1+x^2}dx](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_140.jpg)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{1+x^2}{1+x^2}dx+\frac{1}{2}\int_0^1\frac{1}{1+x^2}dx](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_141.jpg)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{1+x^2}{1+x^2}dx+\frac{1}{2}\int_0^1\frac{1}{1+x^2}dx](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_142.jpg)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1dx+\frac{1}{2}\int_0^1\frac{1}{1+x^2}dx](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_143.jpg)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\left[x\right]_0^1+\frac{1}{2}\left[tan^{-1}x\right]_0^1](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_144.jpg)
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 33。 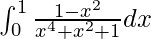
解决方案:
We have,
I = ![]()
I = ![]()
I = 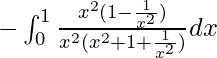
I = 
I = 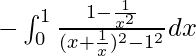
I = ![Rendered by QuickLaTeX.com -\left[\frac{1}{2}\log|\frac{x+\frac{1}{x}-1}{x+\frac{1}{x}+1}|\right]^1_0](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_157.jpg)
I = ![Rendered by QuickLaTeX.com -\left[\frac{1}{2}\log|\frac{x^2-x+1}{x^2+x+1}|\right]^1_0](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_158.jpg)
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 34。 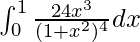
解决方案:
We have,
I = ![]()
Let 1 + x2 = t. So, we have
=> 2x dx = dt
Now, the lower limit is, x = 0
=> t = 1 + x2
=> t = 1 + 02
=> t = 1 + 0
=> t = 1
Also, the upper limit is, x = π
=> t = 1 + x2
=> t = 1 + 12
=> t = 1 + 1
=> t = 2
So, the equation becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = 1
Therefore, the value of ![]() is 1.
is 1.
问题 35。 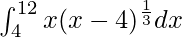
解决方案:
We have,
I = ![]()
Let x – 4 = t3. So, we have
=> dx = 3t2 dt
Now, the lower limit is, x = 4
=> t3 = x – 4
=> t3 = 4 – 4
=> t3 = 0
=> t = 0
Also, the upper limit is, x = 12
=> t3 = x – 4
=> t3 = 12 – 4
=> t3 = 8
=> t = 2
So, the equation becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![Rendered by QuickLaTeX.com 3\left[\frac{t^7}{7}+t^4\right]_{0}^{2}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_184.jpg)
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 36。 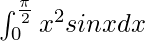
解决方案:
We have,
I = ![]()
On using integration by parts, we get
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = π + 0 – 0 – 0 – 2
I = π – 2
Therefore, the value of ![]() is π – 2.
is π – 2.
问题 37。 
解决方案:
We have,
I = ![]()
Let x = cos 2t. So, we have
=> dx = – 2 sin 2t dt
Now, the lower limit is, x = 0
=> cos 2t = x
=> cos 2t = 0
=> 2t = π/2
=> t = π/4
Also, the upper limit is, x = 1
=> cos 2t = x
=> cos 2t = 1
=> 2t = 0
=> t = 0
So, the equation becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![Rendered by QuickLaTeX.com 2\left[t-\frac{sin^2t}{2}\right]^{\frac{\pi}{4}}_{0}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_205.jpg)
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 38。 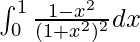
解决方案:
We have,
I = ![]()
I = 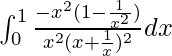
I = 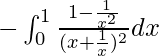
Let x + 1/x = t. So, we have
=> (1 – 1/x2)dx = dt
Now, the lower limit is, x = 0
=> t = x + 1/x
=> t = ∞
Also, the upper limit is, x = 1
=> t = x + 1/x
=> t = 1 + 1
=> t = 2
So, the equation becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 39。 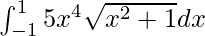
解决方案:
We have,
I = ![]()
Let x5 + 1 = t. So, we have
=> 5x4 dx = dt
Now, the lower limit is, x = –1
=> t = x5 + 1
=> t = (–1)5 + 1
=> t = –1 + 1
=> t = 0
Also, the upper limit is, x = 1
=> t = x5 + 1
=> t = (1)5 + 1
=> t = 1 + 1
=> t = 2
So, the equation becomes,
I = ![]()
I = ![Rendered by QuickLaTeX.com \left[\frac{2}{3}t^{\frac{3}{2}}\right]_{0}^{2}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_224.jpg)
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 40。 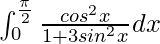
解决方案:
We have,
I = ![]()
I = ![]()
Let tan x = t. So, we have
=> sec2 x dx = dt
Now, the lower limit is, x = 0
=> t = tan x
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = tan x
=> t = tan π/2
=> t = ∞
So, the equation becomes,
I = ![]()
I = ![]()
I = ![]()
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.
问题 41。 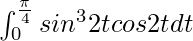
解决方案:
We have,
I = ![]()
Let sin 2t = u. So, we have
=> 2 cos 2t dt = du
=> cos 2t dt = du/2
Now, the lower limit is, x = 0
=> u = sin 2t
=> u = sin 0
=> u = 0
Also, the upper limit is, x = π/4
=> u = sin 2t
=> u = sin π/2
=> u = 1
So, the equation becomes,
I = ![]()
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{u^4}{4}\right]_{0}^{1}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_20_Definite_Integrals_%E2%80%93_Exercise_20.2_%7C_Set_2_243.jpg)
I = ![]()
I = ![]()
Therefore, the value of ![]() is
is ![]() .
.