第 12 类 RD Sharma 解决方案 - 第 9 章连续性 - 练习 9.2 |设置 1

问题 1. 证明函数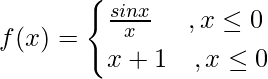$f(x)=\begin{cases}\frac{sinx}{x} \ \ \ \ ,x\le0\\x+1\ \ \ ,x\le0\end{cases}$处处连续。

解决方案：

We know sin x/ x is continuous everywhere since it is the composite function of the functions sin x and x which are continuous.

When x > 0, we have f(x) = x + 1.

Given that $f(x)=\binom{\frac{sinx}{x}, x < 0}{x + 1, x \geq 0}$

Now, (LHL at x = 0) = lim_{{x ⇢ 0^–}} f(x)

= lim_{{h ⇢ 0}} f(0 – h)

= lim_{{h ⇢ 0}} f(-h)

= lim{h ⇢ 0} (sin (-h)/(-h))

= lim_{{h ⇢ 0}} (sin h/ h)

= 1

(RHL at x = 0) = lim_{{x ⇢ 0+}} f(x)

= lim_{{h ⇢ 0}} f(0 + h)

= lim_{{h ⇢ 0}} f(h)

= lim_{{h ⇢ 0}} (h + 1)

= 1

and, f(0) = 0 + 1 = 1.

We observe that: lim_{{x ⇢ 0^–}}f(x) = lim_{{x ⇢ 0⁺}} f(x) = f(0).

Therefore, f(x) is everywhere continuous.

问题2.讨论函数的连续性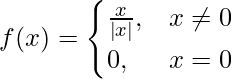$f(x)=\begin{cases}\frac{x}{\left| x \right|}, & x \neq 0 \\ 0 , & x = 0\end{cases}$ .

解决方案：

We have, 

$f(x)=\begin{cases}1 \ \ \ \ \ \ \ , x > 0 \\ - 1 \ \ \ \ , x < 0 \\ 0 \ \ \ \ \ \ \ , x = 0\end{cases}$

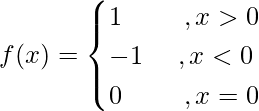
Now: (LHL at x = 0) =  lim_{{x ⇢ 0^–}} f(x)

= lim_{{h ⇢ 0}} f(0 – h)

= lim_{{h ⇢ 0}} f(–h)

= lim_{{h⇢ 0}} (–1)

= –1

(RHL at x = 0) = lim_{{x ⇢ 0⁺}} f(x)

= lim_{{h ⇢ 0}} f(0 + h)

= lim_{{h ⇢ 0}} (1)

= 1

We observe that, lim_{{x ⇢ 0^–}} f(x) ≠ lim_{{x ⇢ 0⁺}} f(x).

Therefore, f(x) is discontinuous at x = 0.

问题 3. 找出以下函数的不连续点（如果有）：

（一世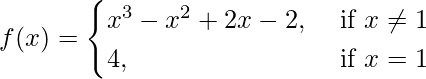） $f(x)=\begin{cases}x^3 - x^2 + 2x - 2, & \text{ if }x \neq 1 \\ 4 , & \text{ if } x = 1\end{cases}$

解决方案：

Since a polynomial function is everywhere continuous.

At x = 1, we have

(LHL at x = 1) = lim_{{x ⇢ 1^–}} f(x)

= lim_{{h ⇢ 0}} f(1 – h)

= lim_{{h ⇢ 0}} ((1 – h)³ – (1 – h )² + 2(1 – h) – 2)

= 1 – 1 + 2 – 2

= 0

(RHL at x = 1) = lim_{{x ⇢ 1⁺}} f(x)

= lim_{{h ⇢ 0}} f(1 + h)

= lim{h ⇢ 0} ((1 + h)³ – (1 + h )² + 2(1 + h) – 2)

= 1 – 1 + 2 – 2

= 0

Also, f(1) = 4.

We observe that, lim_{{x ⇢ 0^–}} f(x) = lim_{{x ⇢ 0⁺}} f(x) ≠  f(1).

Therefore, f(x) is discontinuous only at x = 1.

(二) 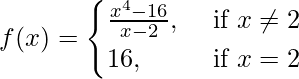$f( x ) =\begin{cases}\frac{x^4 - 16}{x - 2}, & \text{ if } x \neq 2 \\ 16 , & \text{ if } x = 2\end{cases}$

解决方案：

When x ≠ 2 then 

f(x) = $\frac{x^4 - 16}{x - 2}$

= $\frac{x^4 - 2^4}{x - 2}$

= $\frac{\left( x^2 + 4 \right)\left( x - 2 \right)\left( x + 2 \right)}{x - 2}$

= (x² + 4)(x + 2)

Since a polynomial function is everywhere continuous, (x² + 4) and (x + 2) are  continuous everywhere.

So, the product function (x² + 4)(x + 2) is continuous.

Thus, f(x) is continuous at every x ≠ 2 .  

We observe that lim_{x->2-}f(x) = lim_{x->2+}f(x) = f(2)

Therefore, f(x) is discontinuous only at x = 2.

㈢ 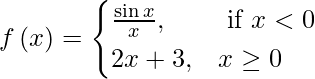$f\left( x \right) = \begin{cases}\frac{\sin x}{x}, & \text{ if } x < 0 \\ 2x + 3, & x \geq 0\end{cases}$

解决方案：

When x < 0, then f(x) = sin x/ x.

Since sin x as well as the identity function x are everywhere continuous, the quotient function sin x/x is continuous at each x < 0.  

For x > 0, f(x) becomes a polynomial function. Therefore, f(x) is continuous at each x > 0.

We have: (LHL at x = 0) = lim_{x->0-}f(x)

= lim_{{h -> 0}} f(0 – h)

= lim_{{h -> 0}} f (-h)

= lim_{{h -> 0}} (sin(-h)/(-h))

= lim_{{h -> 0}} (sin h/h)

= 1

(RHL at x = 0) = lim_{_{x -> 0+}} f(x)

= lim_{{h -> 0}} f(0 + h)

= lim_{{h -> 0}} f(h)

= lim_{{h -> 0}} (2h + 3)

= 3

We observe that lim_{{x -> 0-}} f(x) ≠ lim_{{x -> 0+}} f(x)

Therefore, f(x) is discontinuous only at x = 0.

(四) 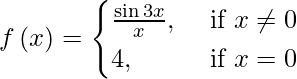$f\left( x \right) = \begin{cases}\frac{\sin 3x}{x}, & \text{ if } x \neq 0 \\ 4 , & \text{ if } x = 0\end{cases}$

解决方案：

At x ≠ 0, then f(x) = sin 3x/ x.

Since the functions sin 3x and x are everywhere continuous. So, the quotient function sin 3x/x is continuous at each x ≠ 0.  

We have: (LHL at x = 0) = lim_{{x -> 0+}} f(x)

= lim_{{h -> 0}} f(0 + h)

= lim_{{h -> 0}} f(h)

= lim_{{h -> 0}} (sin 3h/h)

= lim_{{h -> 0}} 3 (sin h/h) = 3

(RHL at x = 0) = lim_{{x -> 0+}} f(x)

= lim_{{h -> 0}} f(0 + h)

= lim_{{h -> 0}} f(h)

= lim_{{h -> 0}} (sin 3h/h)

= lim_{{h -> 0}} 3 (sin 3h/h)

= 3

Also, f(0) = 4.   

We observe that lim_{{x -> 0-}} f(x) = lim_{{x -> 0+}} f(x) = f(0)

Therefore, f(x) is discontinuous only at x = 0.

(五) 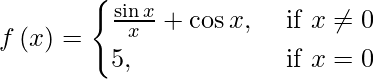$f\left( x \right) = \begin{cases}\frac{\sin x}{x} + \cos x, & \text{ if } x \neq 0 \\ 5 , & \text { if } x = 0\end{cases}$

解决方案：

When x ≠ 0, then f(x) = sin x/ x + cos x.

We know that sin x as well as cos x are everywhere continuous. Thus, the given function is continuous at each x ≠ 0.

Let us consider the point x = 0.

Given: $f\left( x \right) = \binom{\frac{\text{ sin } x}{x} + \ \text{ cos } x, \text{ if } x \neq 0}{5, \text{ if } x = 0 }$

We have: (LHL at x = 0) = lim_{{x -> 0-}} f(x)

= lim_{{h -> 0}} f(0 – h)

= lim_{{h -> 0}} f(-h)

= lim_{{h -> 0}} [(sin (-h)/(-h)) + cos (-h)]

= lim_{{h -> 0}} sin(-h)/(-h) + lim_{{h -> 0}} cos(-h)

= 1 + 1

= 2

(RHL at x = 0) = lim_{{x -> 0+}} f(x)

= lim_{{h -> 0}} f(0 + h)

= lim_{{h -> 0}} f(h)

= lim_{{h -> 0}} [(sin h/h) + cos (-h)]

= lim_{{h -> 0}} sin h/h + lim_{{h -> 0}} cos(-h)

= 1 + 1

= 2

Also, f(0) = 5.

We observe that lim_{{x -> 0-}} f(x) = lim_{{x -> 0^+}} f(x) ≠ f(0)

Therefore, f(x) is discontinuous only at x = 0.

(六) 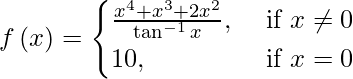$f\left( x \right) = \begin{cases}\frac{x^4 + x^3 + 2 x^2}{\tan^{- 1} x}, & \text{ if } x \neq 0 \\ 10 , & \text{ if } x = 0\end{cases}$

解决方案：

When x ≠ 0, then $f( x) = \frac{x^4 + x^3 + 2 x^2}{tan^{- 1} x}$

x⁴ + x³ + 2x² being a polynomial function is continuous everywhere. 

Also, tan^-1x is everywhere continuous.

Let us consider the point x = 0.

We have: 

(LHL at x = 0) = lim_{{x -> 0-}} f(x)

= lim_{{h -> 0}} f(0 – h)

= lim_{{h -> 0}} f(-h)

= $\lim_{h \to 0} \left( \frac{\left( - h \right)^4 + \left( - h \right)^3 + 2 \left( - h \right)^2}{\tan^{- 1} \left( - h \right)} \right)$

= $\lim_{h \to 0} \left( \frac{\left( h \right)^3 - \left( h \right)^2 + 2\left( h \right)}{- \frac{\tan^{- 1} \left( h \right)}{h}} \right)$

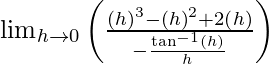
= 0

(RHL at x = 0) = lim_{{x -> 0+}} f(x)

= lim_{{h -> 0}} f(0 + h)

= lim_{{h -> 0}} f(h)

= $\lim_{h \to 0} \left( \frac{\left( h \right)^4 + \left( h \right)^3 + 2 \left( h \right)^2}{\tan^{- 1} \left( h \right)} \right)$

= $\lim_{h \to 0} \left( \frac{\left( h \right)^3 + \left( h \right)^2 + 2\left( h \right)}{\frac{\tan^{- 1} \left( h \right)}{h}} \right)$

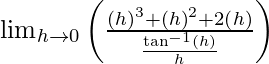
= 0

Also, f(0) = 10.

We observe that lim_{{x -> 0-}} f(x) = lim_{{x -> 0⁺}} f(x) ≠ f(0)

Therefore, f(x) is discontinuous only at x = 0.

(七) 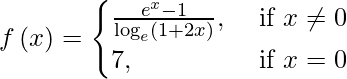$f\left( x \right) = \begin{cases}\frac{e^x - 1}{\log_e (1 + 2x)}, & \text{ if }x \neq 0 \\ 7 , & \text{ if } x = 0\end{cases}$

解决方案：

We have,

$\lim_{x \to 0} f\left( x \right) = \lim_{x \to 0} \frac{e^x - 1}{\log_e \left( 1 + 2x \right)}$

= $\lim_{x\to0}\frac{\left( \frac{e^x - 1}{x} \right)}{\left( \frac{2 \log_e \left( 1 + 2x \right)}{2x} \right)}$

= $\frac{1}{2} \times \frac{\lim_{x \to 0} \left( \frac{e^x - 1}{x} \right)}{\lim_{x \to 0} \left( \frac{\log_e \left( 1 + 2x \right)}{2x} \right)}$

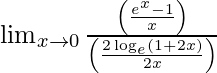
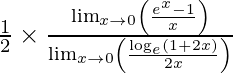
= 1/2

It is given that f(0) = 7.

We observe that lim_{{x -> 0}} f(x) ≠ f(0)

Therefore, f(x) is discontinuous only at x = 0.

(八) 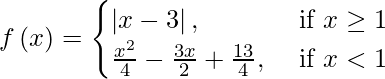$f\left( x \right) = \begin{cases}\left| x - 3 \right|, & \text{ if } x \geq 1 \\ \frac{x^2}{4} - \frac{3x}{2} + \frac{13}{4}, & \text{ if } x < 1\end{cases}$

解决方案：

At x > 1, f(x) being a modulus function is continuous for each x > 1.

When x < 1, then f( x ) being a composite of polynomial and continuous functions would be continuous.

At x = 1, we have

(LHL at x = 1) = lim_{{x -> 1-}} f(x)

= lim_{{h -> 0}} f(1 – h)

= $\lim_{h\to0} \left[ \frac{\left( 1 - h \right)^2}{4} - \frac{3\left( 1 - h \right)}{2} + \frac{13}{4} \right]$    

= 1/4 – 3/2 + 13/4

= 2

(RHL at x = 1) = lim_{{x -> 1+}} f(x)

= lim_{{h -> 0}} f(1 + h)

= lim_{{h -> 0}} |1 + h – 3| 

= |-2|

= 2

Also f(1) = |1 – 3| = |- 2| = 2

We observe that, lim_{{x -> 1-}} f(x) = lim_{{x -> 1+}} f(x) = f(1)

Therefore, the given function is everywhere continuous.

(九) 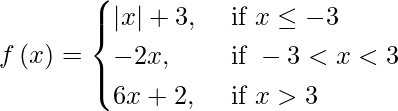$f\left( x \right) = \begin{cases}\left| x \right| + 3 , & \text{ if } x \leq - 3 \\ - 2x , & \text { if } - 3 < x < 3 \\ 6x + 2 , & \text{ if } x > 3\end{cases}$

解决方案：

f(x) being a modulus function is continuous for each x ≤ – 3.

At – 3 < x < 3 f(x) being a  polynomial function is continuous.

At x > 3, f(x) being a  polynomial function is continuous.

At x = 3, 

We have: (LHL at x = 3) = lim_{{x -> 3-}} f(x)

= lim_{{h -> 0}} f(3 – h)

= lim_{{h -> 0}} -2(3 – h)

= -6

(RHL at x = 3) = lim_{{x -> 3+}} f(x)

= lim_{{h -> 0}} f(3 + h)

= lim_{{h -> 0}} 6(3 + h) + 2

= 20

We observe that lim_{{x -> 3-}} f(x) ≠ lim_{{x -> 3+}} f(x)

Therefore, f(x) is discontinuous only at x = 3.

（X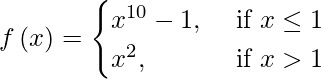） $f\left( x \right) = \begin{cases}x^{10} - 1, & \text{ if } x \leq 1 \\ x^2 , & \text{ if } x > 1\end{cases}$

解决方案：

According to the question it is given that function f is defined at all the points of the real line.

Let us considered c be a point on the real line.

Case I: If c< 1, then f(c) = c¹⁰ −1 and 

lim_{{x-> c}} f(x) = lim_{x->c} (x¹⁰ – 1)           

= c¹⁰ −1.

∴ lim_{x->c} f(x) = f(c)

Hence, f is continuous for all x < 1.

Case II: If c = 1, then the left hand limit of f at x = 1.

The right hand limit of f at x = 1 is, lim_(x->1) f(x) = lim_(x->1) (x²) = 1² = 1

So we conclude that the left and right hand limit of f at x = 1 do not coincide. So, f is not continuous at x = 1.

Case III: If c>1, then f(c) = c²

lim_(x->c) f(x) = lim_(x->c) f(c) = c²

∴ lim_(x->c) f(x) = f(c)

Therefore, f(x) is discontinuous only at x = 1. 

(十一) 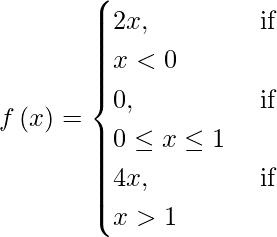$f\left( x \right) = \begin{cases}2x , & \text{ if } & x < 0 \\ 0 , & \text{ if } & 0 \leq x \leq 1 \\ 4x , & \text{ if } & x > 1\end{cases}$

解决方案：

Let us considered a be a point on the real line.

Case I: if a < 0, then f(c) = 2a.

lim_{x->a}(a) = 2a.

∴ lim_{{N -> 0}}f(x) = f(a)

So, f is continuous at all points such that x < 0.

Case II: If 0 < a < 1 then f(x) and lim_{x->a}f(x)=lim_{x->a}(0)=0        .

∴ lim_{x->a}f(x)=f(a)

So, f is continuous at all points of the interval (0, 1).

Case III:  If a =1 then f(a) = f(1) = 0.

The left hand limit of f at x = 1 is,  

lim_{x->1}f(x) = lim_{x->1}f(1) 

The right hand limit of f at x = 1 is,

lim_{x->1}f(x) = lim_{x->1}(4x) = 4(1) = 4

So we conclude that LHL ≠ RHL. Thus, f is not continuous at x = 1.

Case IV: If a > 1, then f(a) = 4a and lim_{x->a}f(4x) = 4a        .

∴ lim_{x->a}f(x) = f(a)

So, f(x) is discontinuous only at x = 1.

(十二) 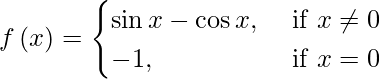$f\left( x \right) = \begin{cases}\sin x - \cos x , & \text{ if } x \neq 0 \\ - 1 , & \text{ if } x = 0\end{cases}$

解决方案：

It is evident that f is defined at all points of the real line. Let p be a real number.

Case I:  if p ≠ 0 , then f (p) = sin p – cos p 

lim_{{x → p}}f(x) = lim_{x→p}( sin x – cos x ) = sin p – cos p 

∴ lim_{{x →p}}f(x) = f(p) 

Therefore, f is continuous at all points x, such that x ≠ 0.

Case II: if p = 0 , then f (0) = – 1.

lim_{{x →0-}}f(x) = lim_{{x →0^-}}(sin x – cos x) = sin 0 – cos 0 = 0 – 1 = -1

lim_{{x →0+}}f(x) = lim_{{x →0}}(sin x – cos x) = sin 0 –  cos 0 = 0 – 1 = -1

We observe that: lim_{{x →0-}} f (x) = lim_{{x →0+}}f (x)= f(0)

Therefore, f is a continuous function everywhere.

(十三) 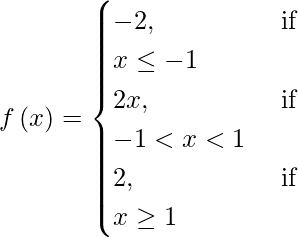$f\left( x \right) = \begin{cases}- 2 , & \text{ if }& x \leq - 1 \\ 2x , & \text{ if } & - 1 < x < 1 \\ 2 , & \text{ if } & x \geq 1\end{cases}$

解决方案：

The given function is defined at all points of the real line. Let us considered a be a point on the real line.

Case I: If  a < -1 then f(a)= -2 and  lim_{x->a}(x) = lim_{x->a}(-2) = -2

∴ lim_{x->a}f(x) = f(a)

 f is continuous for all x < −1.

Case II:  If a =1 then f(a) = f(-1) = -2

LHL = lim_{x->-1}f(x) = lim_{x->-1}f(-2) = -2

RHL = lim_{x->-1}f(x) = lim_{x->-1}f(2x) = 2(-1) = -2

We observe that lim_{x->-1}f(x) = f(-1)

Therefore, f is continuous at x = −1.

Case III: if -1 < a < 1,then f(a) = 2a

lim_{x->a}f(x) = lim_{x->a}f(2x) = 2a

∴ lim_{x->a}f(x) = f(a)

Therefore, f is continuous at all points of the interval (−1, 1).

Case IV: if a = 1, then f(c) = f(1) = 2(1) = 2.

LHL = lim_{x->1}f(x) = lim_{x->1}2 = 2

RHL = lim_{x->1}f(x) = lim_{x->1}2 = 2

We observe that: lim_{x->1}f(x) = lim_{x->1}f(c)

Therefore, f is continuous at x = 2.

Therefore, f is a continuous function everywhere.

问题 4. 在下面，确定定义中涉及的常数的值，使得给定的函数是连续的：

（一世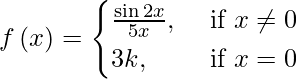） $f\left( x \right) = \begin{cases}\frac{\sin 2x}{5x}, & \text{ if } x \neq 0 \\ 3k , & \text{ if } x = 0\end{cases}$

解决方案：

If f( x ) is continuous at x = 0, then  

⇒ lim{x -> 0} f(x) = f(0)

⇒ lim_{{x -> 0}} sin 2x/5x = f(0)

⇒ lim_{{x -> 0}} 2 sin 2x/10x = f(0)

⇒ 2/5 lim_{{x -> 0}} sin 2x/2x = f(0)

⇒ k = 2/15

(二) 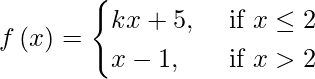$f\left( x \right) = \begin{cases}kx + 5, & \text{ if } x \leq 2 \\ x - 1, & \text{ if } x > 2\end{cases}$

解决方案：

If f(x) is continuous at x = 2, then  

lim_{{x -> 2-}} f(x) = lim_{{x -> 2+}} f(x)

⇒ lim_{{h -> 0}} (k (2 – h) + 5) = lim_{{h -> 0}} (2 + h -1)

⇒ lim_{{h -> 0}} f(2 – h) = lim_{{h -> 0}} f(2 + h)

⇒ 2k + 5 = 1

⇒ 2k = – 4

⇒  k = – 2

㈢ 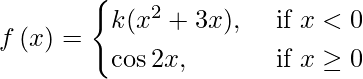$f\left( x \right) = \begin{cases}k( x^2 + 3x), & \text{ if } x < 0 \\ \cos 2x , & \text{ if } x \geq 0\end{cases}$

解决方案：

If f(x) is continuous at x = 0, then  

lim_{{x -> 0-}} f(x) = lim_{{x -> 0+}} f(x)

⇒ lim_{{h -> 0}} f(-h) = lim_{{h -> 0}} f(h)

⇒ $\lim_{h -> 0} \left( k\left( \left( - h \right)^2 - 3h \right) \right) = lim_{h -> 0} \left( \cos 2h \right)$

⇒ 0 = 1, which is not possible

Therefore, the given function is not continuous for any value of k.

(四) 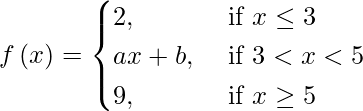$f\left( x \right) = \begin{cases}2 , & \text{ if } x \leq 3 \\ ax + b, & \text{ if } 3 < x < 5 \\ 9 , & \text{ if } x \geq 5\end{cases}$

解决方案：

If f(x) is continuous at x = 3 and 5, then  

lim_{{x -> 3-}} f(x) = lim_{{x -> 3+}} f(x)

and  lim_{{x -> 5-}} f(x) = lim_{{x -> 5+}} f(x)

⇒ lim_{{h -> 0}} f(3 – h) = lim_{{h -> 0}} f(3 + h)               

 and lim_{{h -> 0}} f(5 – h) = lim_{{h -> 0}} f(5 + h)

⇒ 2 = 3a + b and 5a + b = 9

⇒ 2 = 3a + b and 5a + b = 9

⇒ a = 7/2 and  b = -17/2.

(五) 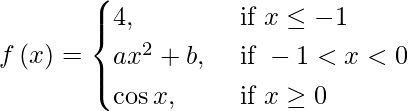$f\left( x \right) = \begin{cases}4 , & \text{ if } x \leq - 1 \\ a x^2 + b, & \text{ if } - 1 < x < 0 \\ \cos x, &\text{ if }x \geq 0\end{cases}$

解决方案：

If  f(x) is continuous at x = −1 and 0, then  

lim_{{x -> -1-}} f(x) = lim_{{x -> – 1+}} f(x) and lim_{{x -> 0-}} f(x) = lim_{{x -> 0+}} f(x)

⇒ lim_{{h -> 0}} f(-1 – h) = lim_{{h -> 0}} f(-1 + h) and lim_{{h -> 0}} f(-h) = lim_{{h -> 0}} f(h)

⇒ lim_{{h -> 0}} (4) = lim_{{h -> 0}} (a (-1 + h)² + b) 

Also, $\lim_{h -> 0} \left( a \left( - h \right)^2 + b \right) = \lim_{h -> 0} \left( \cos h \right)$

⇒ 4 = a + b  and  b = 1

⇒ a = 3 and  b = 1.

(六) 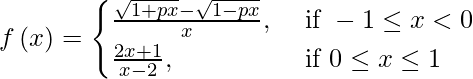$f\left( x \right) = \begin{cases}\frac{\sqrt{1 + px} - \sqrt{1 - px}}{x}, & \text{ if } - 1 \leq x < 0 \\ \frac{2x + 1}{x - 2} , & \text{ if } 0 \leq x \leq 1\end{cases}$

解决方案：

If f(x) is continuous at x = 0, then $\lim_{x \to 0^-} f( x ) = \lim_{x \to 0^+} f( x )$

⇒ $\lim_{h \to 0} f\left( - h \right) = \lim_{h \to 0} f\left( h \right)$

⇒ $\lim_{h \to 0} \left( \frac{\sqrt{1 - ph} - \sqrt{1 + ph}}{- h} \right) = \lim_{h \to 0} \left( \frac{2h + 1}{h - 2} \right)$

⇒ $\lim_{h \to 0} \left( \frac{\left( \sqrt{1 - ph} - \sqrt{1 + ph} \right)\left( \sqrt{1 - ph} + \sqrt{1 + ph} \right)}{- h\left( \sqrt{1 - ph} + \sqrt{1 + ph} \right)} \right) = \lim_{h \to 0} \left( \frac{2h + 1}{h - 2} \right)$

⇒ $\lim_{h \to 0} \left( \frac{\left( 1 - ph - 1 - ph \right)}{- h\left( \sqrt{1 - ph} + \sqrt{1 + ph} \right)} \right) = \lim_{h \to 0} \left( \frac{2h + 1}{h - 2} \right)$

⇒ $\lim_{h \to 0} \left( \frac{\left( - 2ph \right)}{- h\left( \sqrt{1 - ph} + \sqrt{1 + ph} \right)} \right) = \lim_{h \to 0} \left( \frac{2h + 1}{h - 2} \right)$

⇒ $\lim_{h \to 0} \left( \frac{\left( 2p \right)}{\left( \sqrt{1 - ph} + \sqrt{1 + ph} \right)} \right) = \lim_{h \to 0} \left( \frac{2h + 1}{h - 2} \right)$

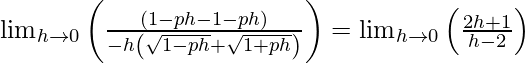
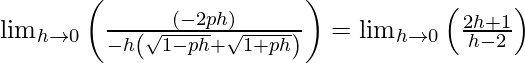
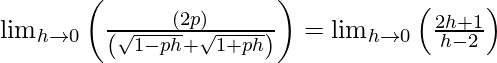
⇒ 2p/2 = -1/2

⇒ p = -1/2.

(七) 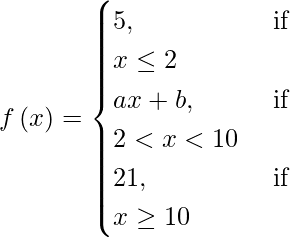$f\left( x \right) = \begin{cases}5 , & \text{ if } & x \leq 2 \\ ax + b, & \text{ if } & 2 < x < 10 \\ 21 , & \text{ if } & x \geq 10\end{cases}$

解决方案：

If f(x) is continuous at x = 2 and x = 10, then  

lim_{{x -> 2-}} f(x) = lim_{{x -> 2+}} f(x) and lim_{{x -> {10}^–}} f(x) = lim_{{x -> {10}+}} f(x)

⇒ lim_{{h -> 0}} f(2 – h) = lim_{{h -> 0}} f(2 + h) and lim_{{h -> 0}} f(10 – h) = lim_{{h -> 0}} f(10 + h)

⇒ lim_{{h -> 0}} (5) = lim_{{h -> 0}} (a (2 + h) + b)

And lim_{{h -> 0}} a (10 – h) + b = lim_{{h -> 0}} (21)

On solving equations, we get,

⇒ a = 2  and  b = 1.

(八) 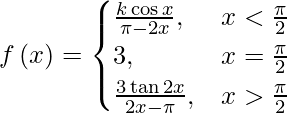$f\left( x \right) = \begin{cases}\frac{k \cos x}{\pi - 2x} , & x < \frac{\pi}{2} \\ 3 , & x = \frac{\pi}{2} \\ \frac{3 \tan 2x}{2x - \pi}, & x > \frac{\pi}{2}\end{cases}$

解决方案：

If f(x) is continuous at x = π/2, then  

lim_{{x -> π/2-}} f(x) = f(π/2)

⇒ lim_{{h -> 0}} f(π/2 – h) = f(π/2)

⇒ lim_{{h -> 0}} f(π/2 – h) = 3

⇒ $\lim_{h \to 0} \left[ \frac{k \cos \left( \frac{\pi}{2} - h \right)}{\pi - 2\left( \frac{\pi}{2} - h \right)} \right] = 3$

⇒ $\lim_{h \to 0} \left[ \frac{k \sin h}{\pi - \pi + 2h} \right] = 3$

⇒ lim_{{h -> 0}} (k sin h/2h) = 3

⇒ k/2 lim_{{h -> 0}} sin h/h =3

⇒ k/2 = 3

⇒ k = 6

问题 5.函数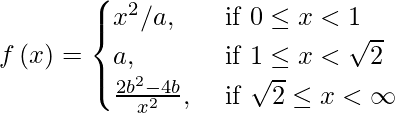$f\left( x \right) = \begin{cases}x^2 /a , & \text{ if } 0 \leq x < 1 \\ a , & \text{ if } 1 \leq x < \sqrt{2} \\ \frac{2 b^2 - 4b}{x^2}, & \text{ if } \sqrt{2} \leq x < \infty\end{cases}$在 (0, ∞) 上是连续的，然后找到 a 和 b 的最合适的值。

解决方案：

Given that f is continuous on ( 0, ∞ ).

So, f is continuous at x = 1 and x = √2.

At x = 1, we have lim_{{x -> 1-}} f(x)

= lim_{{h -> 0}} f(1 – h)

= lim_{{h -> 0}} [(1 – h)²/a]

= 1/a

 At x = √2, we have

lim_{{x -> √2-}} f(x) = lim_{{h -> 0}} f(√2 + h)

= lim_{{h -> 0}} (a)

= a

$\lim_{x \to \sqrt{2}^+} f\left( x \right) = \lim_{h \to 0} f\left( \sqrt{2} + h \right) = \lim_{h \to 0} \left[ \frac{2 b^2 - 4b}{\left( \sqrt{2} + h \right)^2} \right] = \frac{2 b^2 - 4b}{2} = b^2 - 2b$

f is continuous at x = 1 and √2.

⇒ 1/a = a and b² – 2b = a

⇒ a² = 1 and b² – 2b = a

⇒ a = ±1  and  b² – 2b = a          . . . (1)

If a = 1, then b² – 2b = 1

⇒ b² – 2b – 1 = 0

⇒ b = $\frac{2 \pm \sqrt{4 + 4}}{2} = \frac{2 \pm 2\sqrt{2}}{2}$ = 1 ± √2

If a = −1, then b² – 2b = – 1

⇒ b² – 2b + 1 = 0

⇒ b = 1

Therefore,  a = −1, b = 1  or a = 1, b = √2.are the most suitable values of a and b.

问题 6. 求 a 和 b 的值，使得函数f(x) 定义为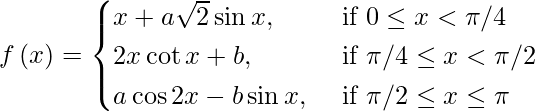$f\left( x \right) = \begin{cases}x + a\sqrt{2}\sin x , & \text{ if }0 \leq x < \pi/4 \\ 2x \cot x + b , & \text{ if } \pi/4 \leq x < \pi/2 \\ a \cos 2x - b \sin x, & \text{ if } \pi/2 \leq x \leq \pi\end{cases}$在 [0, π] 上变得连续。

解决方案：

f is continuous at x = π.

At x = π/4, we have 

lim_{{x -> π/4-}} f(x) = lim_{{h -> 0}} f(π/4 – h)

= lim{h -> 0} [(π/4 – h) + √2a sin (π/4 – h)]

= π/4 + √2a sin π/4

= π/4 + a

= lim_{{h -> 0}} [2 (π/4 + h) cot (π/4 + h) + b]

= [2 π/4 cot π/4 + b]

= π/2 + b

⇒ – b – a = b and π/4 + a = π/2 + b

⇒ a = π/6 and b = -π/12

问题 7.函数f(x) 定义如下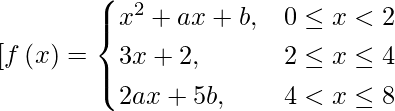： $[f\left( x \right) = \begin{cases}x^2 + ax + b , & 0 \leq x < 2 \\ 3x + 2 , & 2 \leq x \leq 4 \\ 2ax + 5b , & 4 < x \leq 8\end{cases}$ .如果 f 在 [0, 8] 上连续，求 a 和 b 的值。

解决方案：

Given that f is continuous on [0, 8].  

So, f is continuous at x = 2 and x = 4

At x = 2, 

lim_{{x -> 2-}} f(x) = lim_{{h -> 0}} f(2 – h)

= lim_{{h -> 0}} (2 – h)² + a(2 – h) + b

= 4 + 2a + b

lim_{{x -> 2+}} f(x) = lim_{{h -> 0}} f(2 + h)

= lim_{{h -> 0}} [3(2 + h) + h]

= 8

At x = 4, 

lim_{{x -> 4-}} f(x) = lim_{{h -> 0}} f(4 – h)

= lim_{h -> 0} [3(4 – h) + 2]

= 14

lim_{{x -> 4+}} f(x) = lim_{{h -> 0}} f(4 + h)

= lim_{{h -> 0}} [2a(4 + h) + 5b]

= 8a + 5b

So, f is continuous at x = 2 and x = 4.

lim_{{x -> 2-}} f(x) = lim_{{x -> 2+}} f(x)

and, lim_{{x -> 4-}} f(x) = lim_{{x -> 4+}} f(x)

⇒ 4 + 2a + b = 8 and 8a + 5b = 14

⇒ 2a + b = 4 and 8a + 5b = 14

On solving, we get

a = 3 and b = -2