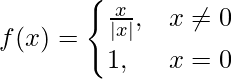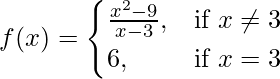第 12 类 RD Sharma 解决方案 - 第 9 章连续性 - 练习 9.1 |设置 1
问题1、在原点测试以下函数的连续性:
解决方案:
Given that
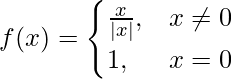
Now, let us consider LHL at x = 0
![]()
![]()
![]()
![]()
Now, let us consider RHL at x = 0
![]()
![]()
So, LHL ≠ RHL
Therefore, f(x) is discontinuous at origin and the discontinuity is of 1st kind.
问题 2.函数f(x) 定义为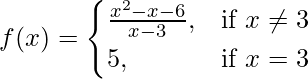 .证明 f(x) 在 x = 3 处是连续的。
.证明 f(x) 在 x = 3 处是连续的。
解决方案:
Given that
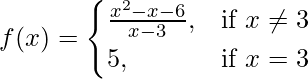
So, here we check the given f(x) is continuous at x = 3,
Now, let us consider LHL at x = 3
![]()
![]()
![]()
![]()
Now, let us consider RHL at x = 3
![]()
![]()
![]()
![]()
So, f(3) = 5
LHL= RHL = f(3)
Therefore, f(x) is continuous at x = 3
问题 3.函数f(x) 定义为
证明 f(x) 在 x = 3 处是连续的。
解决方案:
Given that
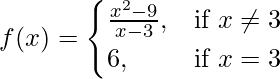
So, here we check the given f(x) is continuous at x = 3,
Now, let us consider LHL at x = 3
![]()
![]()
![]()
![]()
Now, let us consider RHL at x = 3
![]()
![]()
![]()
![]()
So, f(3) = 6
LHL= RHL= f(3)
Therefore, f(x) is continuous at x = 3
问题 4。 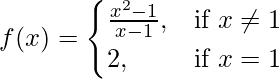
求 f(x) 在 x = 1 处是否连续
解决方案:
Given that
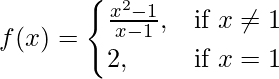
So, here we check the given f(x) is continuous at x = 1,
Now, let us consider LHL at x = 1
![]()
![]()
![]()
![]()
![]()
![]()
Now, let us consider RHL at x = 1
![]()
![]()
![]()
![]()
![]()
![]()
So, f(1) = 2
LHL= RHL = f(1)
Therefore, f(x) is continuous at x = 1
问题 5. 如果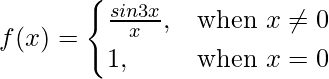
求 f(x) 在 x = 0 处是否连续。
解决方案:
Given that
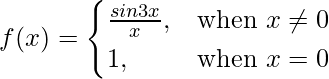
So, here we check the given f(x) is continuous at x = 0,
Now, let us consider LHL at x = 0
![]()
![]()
![]()
Now, let us consider RHL at x = 0
![]()
![]()
So, f(0) = 1
LHL = RHL≠ f(0)
Therefore, f(x) is discontinuous at x = 0.
问题 6. 如果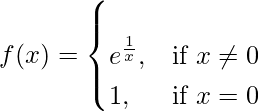
求 f 在 x = 0 处是否连续。
解决方案:
Given that
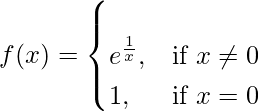
So, here we check the given f(x) is continuous at x = 0,
Now, let us consider LHL at x = 0
![]()
![]()
![]()
Now, let us consider RHL at x = 0
![]()
![]()
So, LHL≠ RHL
Therefore, the f(x) is discontinuous at x = 0.
问题 7. 让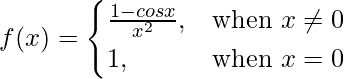
证明 f(x) 在 x = 0 处不连续。
解决方案:
Given that
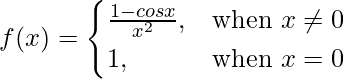
So, here we check the given f(x) is discontinuous at x = 0,
Now, let us consider LHL at x = 0
![]()
![]()
![]()
![]()
![]()
= 2 × 1/4 = 1/2
Now, let us consider RHL at x = 0
![]()
![]()
![]()
![]()
= 2 × 1/4 = 1/2
f(0) = 1
LHL= RHL ≠ f(0)
Therefore, the f(x) is discontinuous at x = 0.
问题 8. 证明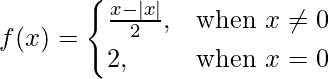 在 x = 0 处不连续。
在 x = 0 处不连续。
解决方案:
Given that
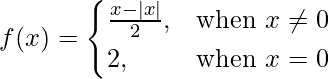
So, here we check the given f(x) is discontinuous at x = 0,
Now, let us consider LHL at x = 0
![]()
![]()
![]()
Now, let us consider RHL at x = 0
![]()
![]()
f(0) = 2
Thus, LHL= RHL≠ f(0)
Therefore, f(x) is discontinuous at x = 0.
问题 9. 证明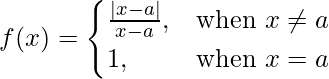 在 x = a 处不连续。
在 x = a 处不连续。
解决方案:
Given that
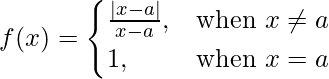
So, here we check the given f(x) is discontinuous at x = a,
Now, let us consider LHL at x = a
![]()
![]()
![]()
Now, let us consider RHL at x = a
![]()
![]()
![]()
Thus, LHS ≠ RHL
Therefore, the f(x) is discontinuous at x = a.
在指定点讨论以下功能的连续性:
问题 10 (i)。 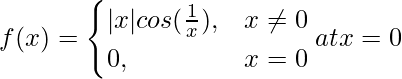
解决方案:
Given that
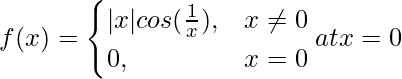
So, here we check the continuity of the given f(x) at x = 0,
Let us consider LHL,
![]()
![]()
![]()
Now, let us consider RHL,
![]()
![]()
f(0) = 0
Thus, LHL= RHL= f(0) = 0
Therefore, f(x) is continuous at x = 0.
问题 10 (ii)。 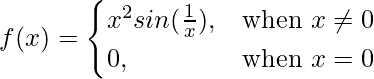 在 x = 0
在 x = 0
解决方案:
Given that
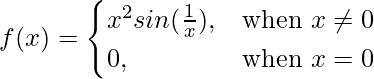
So, here we check the continuity of the given f(x) at x = 0,
Let us consider LHL,
![]()
![]()
Now, let us consider RHL,
![]()
![]()
f(0) = 0
Thus, LHL= RHL = f(0) = 0
Therefore, f(x) is continuous at x = 0.
问题 10 (iii)。 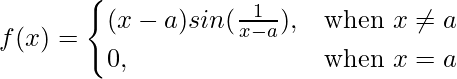 在 x = a
在 x = a
解决方案:
Given that
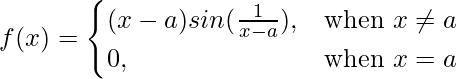
So, here we check the continuity of the given f(x) at x = a,
Let us consider LHL,
![]()
![]()
![]()
Now, let us consider RHL,
![]()
![]()
![]()
f(a) = 0
Thus, LHL= RHL= f(a) = 0
Therefore, f(x) is continuous at x = 0.
问题 10 (iv)。 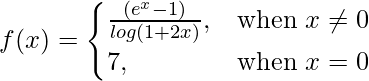 在 x = 0
在 x = 0
解决方案:
Given that
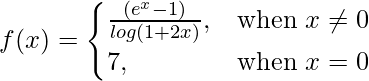
So, here we check the continuity of the given f(x) at x = 0,
![]()
![]()
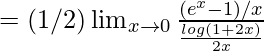
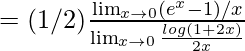
= 1/2 × 1/1 = 1/2
And,
f(0) = 7
![]() ≠ f(0)
≠ f(0)
Therefore, f(x) is discontinuous at x = 0.
问题 10 (v)。 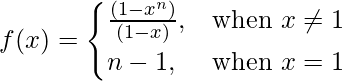 n ∈ N 在 x = 1
n ∈ N 在 x = 1
解决方案:
Given that
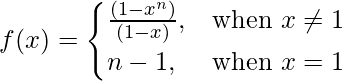
So, here we check the continuity of the given f(x) at x = 1,
Let us consider LHL,
![]()
![]()
![]()
![]()
Now, let us consider RHL,
![]()
![]()
![]()
![]()
f(1) = n – 1
Thus, LHL = RHL ≠ f(1)
Therefore, f(x) is discontinuous at x = 1.
问题 10 (vi)。 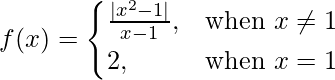 在 x = 1
在 x = 1
解决方案:
Given that
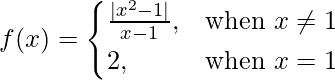
So, here we check the continuity of the given f(x) at x = 1,
Let us consider LHL,
![]()
![]()
![]()
![]()
Now, let us consider RHL,
![]()
![]()
![]()
f(1) = 2
LHL= RHL = f(1) = 2
Therefore, f(x) is discontinuous at x = 1.
问题 10 (vii)。 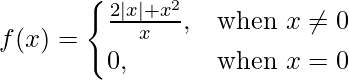 在 x = 0
在 x = 0
解决方案:
Given that
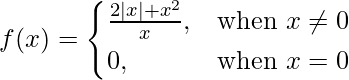
So, here we check the continuity of the given f(x) at x = 0,
Let us consider LHL,
![]()
![]()
![]()
Let us consider RHL,
![]()
![]()
Thus, LHL ≠ RHL
Therefore, f(x) is discontinuous at x = 0.
问题 10 (viii)。 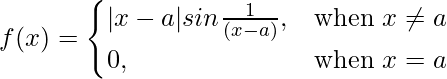 在 x = a
在 x = a
解决方案:
Given that,
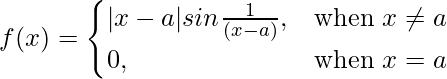
f(x) = (x – a)sin{1/(x – a)}, x > 0
= (x – a)sin{1/(x – a)}, x < 0
= 0, x = a
Let us consider LHL,
![]()
Now, let us consider RHL,
![]()
⇒ ![]()
Therefore, f(x) is continuous at x = a.
问题 11. 证明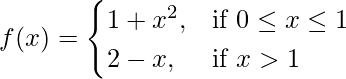 在 x = 1 处不连续。
在 x = 1 处不连续。
解决方案:
Given that,
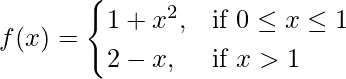
So, here we check the given f(x) is discontinuous at x = 1,
Let us consider LHL,
![]()
![]()
![]()
Now, let us consider RHL,
![]()
![]()
LHL ≠ RHL
Therefore, f(x) is discontinuous at x = 1.
问题 12. 证明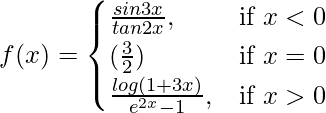 在 x = 0 处是连续的
在 x = 0 处是连续的
解决方案:
Given that,
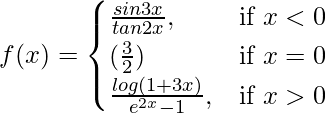
So, here we check the given f(x) is continuous at x = 0,
Let us consider LHL,
![]()
![]()
![]()
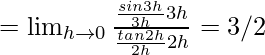
Let us consider RHL,
![]()
![]()
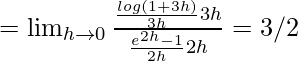
f(0) = 3/2
Thus, LHL = RHL = f(0) = 3/2
Therefore, f(x) is continuous at x = 0.
问题 13. 求函数f 定义为 'a' 的值
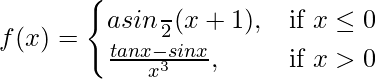 在 x = 0 处是连续的。
在 x = 0 处是连续的。
解决方案:
Given that,
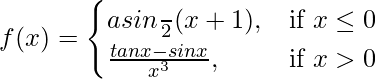
Let us consider LHL,
![]()
![]()
![]()
![]()
Now, let us consider RHL,
![]()
⇒ ![]()
![]()
![]()
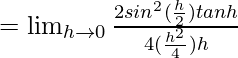
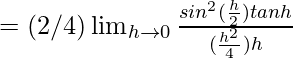
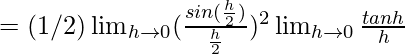
= (1/2) × 1 × 1
⇒ ![]()
If f(x) is continuous at x = 0, then
![]()
⇒ a = 1/2
问题 14. 检查函数的连续性
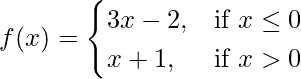 在 x = 0
在 x = 0
还要画出这个函数的图形。
解决方案:
Given that,
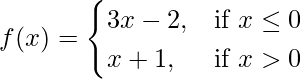
So, here we check the continuity of the given f(x) at x = 0,
Let us consider LHL,
![]()
![]()
![]()
Now, let us consider RHL,
![]()
![]()
LhL ≠ RHL
So, the f(x) is discontinuous.

问题 15. 讨论函数的连续性
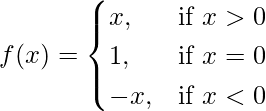 在点 x = 0。
在点 x = 0。
解决方案:
Given that,
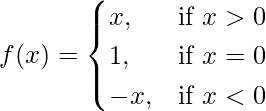
So, here we check the continuity of the given f(x) at x = 0,
Let us consider LHL,
![]()
![]()
Now, let us consider RHL,
![]()
![]()
f(0) = 1
LHL = RHL ≠ f(0)
Hence, the f(x) is discontinuous at x = 0.