第 12 类 RD Sharma 解决方案 - 第 9 章连续性 - 练习 9.2 |设置 2

问题 8. 如果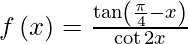$f\left( x \right) = \frac{\tan\left( \frac{\pi}{4} - x \right)}{\cot 2x}$对于 x ≠ π/4，找到在 x = π/4 处可以分配给 f(x) 的值，使得函数f(x) 在 [0, π/2] 中的每个位置都变得连续。

解决方案：

If x ≠ π/4, tan (π/4 – x) and cot2x are continuous in [0, π/2]. Then the function $\frac{\tan \left( \frac{\pi}{4} - x \right)}{\cot 2x}$ is continuous for each x ≠ π/4.

Now, let us assume that the point x = π/4.

We have,

(LHL at x = π/4) = lim_{{x -> π/4-}} f(x)

= lim_{{h -> 0}} f(π/4 – h)

= $\lim_{h \to 0} \left( \frac{\tan\left( \frac{\pi}{4} - \frac{\pi}{4} + h \right)}{\cot\left( \frac{\pi}{2} - 2h \right)} \right)$

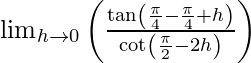
= lim_{{h -> 0}} tan h/tan 2h

= $\lim_{h \to 0} \left( \frac{\frac{\tan \left( h \right)}{h}}{\frac{2 \tan \left( 2h \right)}{2h}} \right)$

= $\frac{1}{2}\left( \frac{\lim_{h \to 0} \frac{\tan \left( h \right)}{h}}{\lim_{h \to 0} \frac{\tan \left( 2h \right)}{2h}} \right)$

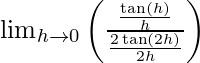
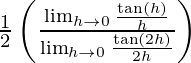
= 1/2

(RHL at x = π/4) = lim_{{x -> π/4+}} f(x)

= lim_{{h -> 0}} f(π/4 + h)

= $\lim_{h \to 0} \left( \frac{\tan \left( \frac{\pi}{4} - \frac{\pi}{4} - h \right)}{\cot \left( \frac{\pi}{2} + 2h \right)} \right)$

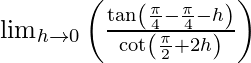
= lim{h -> 0} tan (-h)/tan (-2h)

= lim_{{h -> 0}} tan h/tan 2h

= $\lim_{h \to 0} \left( \frac{\frac{\tan \left( h \right)}{h}}{\frac{2 \tan \left( 2h \right)}{2h}} \right)$

= $\frac{1}{2}\left( \frac{\lim_{h \to 0} \frac{\tan \left( h \right)}{h}}{\lim_{h \to 0} \frac{\tan \left( 2h \right)}{2h}} \right)$

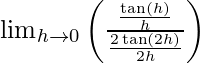
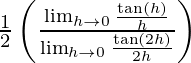
= 1/2

If f(x) is continuous at x = π/4 then

lim_{{x -> π/4-}} f(x) = lim_{{x -> π/4+}} f(x) = f(π/4)

∴  f(π/4) = 1/2

Hence, the function will be everywhere continuous.

问题 9. 讨论函数的连续性$f\left( x \right) = \begin{cases}2x - 1 , & \text { if } x < 2 \\ \frac{3x}{2} , & \text{ if } x \geq 2\end{cases}$ .

解决方案：

When x < 2, f(x) being a polynomial function is continuous.

When x > 2, f(x) being a polynomial and continuous function is continuous.

At x = 2, we have:

(LHL at x = 2) = lim_{{x -> 2-}} f(x)

= lim_{{h -> 0}} f(2 – h)

= lim_{{h -> 0}} (2(2 – h) – 1)

= 4 – 1

= 3

(RHL at x = 2) = lim_{{x -> 2+}} f(x)

= lim_{{h -> 0}} f(2 + h)

= lim_{{h -> 0}} 3 (h + 2)/2

= 3

Also, f(2) = 3(2)/2 = 3

∴ $\lim_{x \to 2^-} f\left( x \right) = \lim_{x \to 2^+} f\left( x \right) = f\left( 2 \right)$

So,  f(x) is continuous at x = 2.

问题 10. 讨论 f(x) = sin |x| 的连续性。

解决方案：

 f is clearly the composition of two functions, f = h o g, where g (x) = |x| and h (x) = sin x

Since, hog(x) = h(g(x)) = h(|x|) = \sin|x|

g(x)=|x| being a modulus function must be continuous for all real numbers.

Let us assume that a be a real number.

Case 1: 

If a > 0 then g(a) = a 

lim_{{x -> c}} (g(x)) = lim_{{x -> c}} (x) = a

So, lim_{{x -> c}} (g(x)) = g(a)

So, g is the continuous on all the points, i.e., x > 0

Case 2: 

If a < 0 then g(a) = -a 

lim_{{x -> c}} (g(x)) = lim_{{x -> c}} (-x) = -a

So, lim_{{x -> c}} (g(x)) = g(a)

So, g is the continuous on all the points x < 0

Case 3: 

If a = 0 then g(a) = g(0) = 0 

lim_{{x -> 0^–}} (g(x)) = lim_{{x -> 0^–}} (-x) = 0

lim_{{x -> 0⁺}} (g(x)) = lim_{{x -> 0⁺}} (x) = 0

So, lim_{{x -> 0^–}} (g(x)) = lim_{{x -> 0⁺}}(g(x)) = g(0)

So, g is continus at point x = 0

So, lim_{{x -> c}} (g(x)) = g(a)

So we conclude that h(x) = sinx is defined for every real number.

Let us considered b be the real number. Now put x = b + k

If x->b , then k ->0

So, h(b) = sin b

lim_{{x -> b}} (h(x)) = lim_{{x -> b}} sin x

= lim_{{k -> 0}} sin (b + k)

= lim_{{k -> 0}} (sinb cos k + cos b sink)

= lim_{{k -> 0}} (sinb cos k) + lim_{{k -> 0}}(cos b sink)

= sinb cos 0 + cos b sin 0

= sin b + 0

= sin b

Hence, lim_{{x -> c}} h(x) = g(c)

So, h is continuous function

Hence, f(x) = hog(x) = h(g(x)) = h(|x|) = sin|x|

问题 11. 证明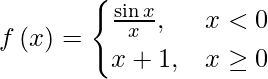$f\left( x \right) = \begin{cases}\frac{\sin x}{x} , & x < 0 \\ x + 1 , & x \geq 0\end{cases}$处处是连续的。

解决方案：

When x < 0, sin x/x being the composite of two continuous functions is continuous.

When x > 0, we have f(x) being a polynomial function is continuous.

At x = 0:

(LHL at x = 0) = lim_{{x -> 0^–}} f(x)

= lim_{{h -> 0}} f(0 – h)

= lim_{{h -> 0}} f(-h)

= lim_{{h -> 0}} (sin (-h)/(-h))

= lim_{{h -> 0}} (sin h/h)

= 1

(RHL at x = 0) = lim_{{x -> 0⁺}} f(x)

= lim_{{h -> 0}} f(0 + h)

= lim_{{h -> 0}} f(h)

 = lim_{{h -> 0}} (h + 1)

= 1

Also, f(x) = 0 + 1 = 1

So we conclude that lim_{{x -> 0^–}} f(x) = lim_{{x -> 0⁺}} f(x) = f(0)

So, f(x) is everywhere continuous.

问题 12. 证明函数g (x) = x − [x] 在所有积分点上都是不连续的。这里 [x] 表示最大整数函数。

解决方案：

 g is defined at all integral points. Let n be an integer. Then,

 g(n) = n − [n]

= n − n

= 0

At x = n, we have:

LHL = lim_{{x -> n^–}}g(x) = lim_{x->n^–}(x – [x])

= lim_{x->n^–}(x) – lim_{_{x->n^–}}[x]

= n − (n − 1)

= 1

RHL = lim_{x->n⁺}g(x) = lim_{x->n⁺} (x – [x])      

= lim_{{x-> n⁺}}(x) – lim_{x->n⁺}[x]

= n − n

= 0

So we conclude that lim_{{x -> 0^–}} f( x ) ≠ lim_{{x -> 0⁺}} f(x)

So, g is discontinuous at all integral points.

问题 13. 讨论以下功能的连续性：

(i) f(x) = sin x + cos x

(ii) f(x) = sin x − cos x

(iii) f(x) = sin x cos x

解决方案：

We know that if g and h are two continuous functions, then g + h, g − h  and g o h are also continuous.

Let g (x) = sin x, defined for every real number.

Let a be a real number. Put x = a + h

If x → a, then h → 0 g(a)=sin a.

lim_{x->a}g(x) = lim_{x->a} sina

 = lim_{h->0} sin (a+h)

 = lim_{h->0}[sin a cos h + cos  a sin h]

 = lim_{h->0}(sin a cos h )+lim_{h->0}(cos a sin h)

= sin a cos 0 + cos a sin 0

= sin (a + 0) 

= sin a

∴ lim_{x->c}g(x) = g(c)

Similarly, cos x can be proved as a continuous function.

So we conclude that

(i) f (x) = g (x) + h (x) = sin x + cos x is a continuous function.

(ii) f (x) = g (x) − h (x) = sin x − cos x is a continuous function.

(iii) f (x) = g (x) h (x) = sin x cos x is a continuous function.

问题 14. 证明 f (x) = cos x ²是一个连续函数。

解决方案：

f can be written as the composition of two functions as f = g o h, where g (x) = cos x and h (x) = x²

∵  (g o h)(x) = g(h (x)) = g(x²) = cos(x²) = f(x)

Let c be a real number.

Then, g(c) = cos c

If  x-> c , then h->0 and lim_{x->c} g(x)

= lim_{x->c}cos c       

= cos c

∴ lim_{x->c}g(x) = g(c)

So, g(x) = cos x is a continuous function.

Now, h(x) = x²

Let k be a real number, then h(k) = k²

lim_x->h(x) = lim_{x->k} x² = k²

∴ lim_{x->k}h(x) = h(k)

So, h is a continuous function.

So, f(x) being a composite of two continuous functions is a continuous function.

问题 15. 证明 f (x) = |cos x|是一个连续函数。

解决方案：

f is the composition of two functions as, f = g o h, where g(x) = |x| and h(x) = cos x

(g o h)(x) = g(h(x)) = g(cos x) = |cos x| = f(x)

Clearly, g(x) being a modulus function would be continuous at all points.

Now, h (x) = cos x. We know that h (x) = cos x is defined for every real number.

Let c be a real number.

Put x = c + h. 

If x → c, then h → 0.

⇒ h(c) = cos c

So, h (x) = cos x is a continuous function.

Therefore, f(x) being a composite of two continuous functions is a continuous function.

问题 16. 找出由 f (x) = |x| 定义的 f 的所有不连续点- |x + 1|。

解决方案：

f is the composition of two functions as f(x) = g(x) – h(x), where g(x) = |x| and h(x) = |x + 1|.

Let c be a real number.

Case I: If c < 0 , then g(c) = -c  and lim_{x->c}g(x) = lim_{x->c} = -c

∴ lim_{x->c}g(x) = g(c)

So, g is continuous at all points x < 0.

Case II: If c < 0 , then g(c) = -c and lim_(x->c)g(x) = lim_(x->c)(-x) = -c

∴ lim_(x->c)g(x) = g(c)

So, g is continuous at all points x > 0.

Case III:  if c = 0 , then g (c) = g(0) = 0

 lim_{x->0-}g(x) = lim_{x->0-}(- x) = 0

 lim_{x->0+}g(x) = lim_{x->0+}(x) = 0

∴ lim_{x->0+}g(x) = lim_{x->0+}(x) = g(0)

So, g is continuous everywhere.

Clearly, h is defined for every real number. Let c be a real number.

Case I: if c < – 1, then h (c) = – (c + 1) 

 lim_{x->c}h (x) = lim_{x->c}[-(x + 1)]    

= -(c + 1)

∴ lim_{{x-> c}} h (x) = h(c) 

Therefore, f being a composite of two continuous functions is a continuous function. 

问题 17. 确定是否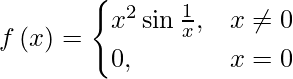$f\left( x \right) = \begin{cases}x^2 \sin\frac{1}{x} , & x \neq 0 \\ 0 , & x = 0\end{cases}$是连续函数吗？

解决方案：

Let us assume that c be a real number.

Case I: If  c ≠ 0 , then f(c)= c² sin (1/c)

lim_{x->c}f(x) = lim_{x->c}(x² sin 1/x) 

= (lim_{x->c}x²) (lim_{x->c} sin 1/x) 

= c² sin (1/c)

lim_{x->c}f(x) = f(c)

So, f is continuous at all points such that x ≠ 0

Case II: If c = 0 then f(0) = 0

lim_{{x -> 0^–}} f(x) = lim_{{x -> 0^–}} (x² sin 1/x) = lim_{{x -> 0}} (x² sin 1/x)

So, -1 ≤ sin 1/x ≤ 1, x ≠ 0

-x² ≤ x²sin 1/x ≤ x²

lim_{{x -> 0}} (-x²) ≤ lim_{{x -> 0}} (x² sin 1/x) ≤ lim_{{x -> 0}} x²

0 ≤ lim_{{x -> 0}} (x² sin 1/x) ≤ 0

lim_{{x -> 0}} (x² sin 1/x) = 0

lim_{{x -> 0^–}} f(x) = 0

Similarly, lim_{{x -> 0⁺}} f(x) = lim_{{x -> 0⁺}} (x² sin 1/x) = lim_{{x -> 0}} (x² sin 1/x) = 0

Thus, f is a continuous function.

问题 18. 给定函数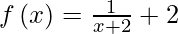$f\left( x \right) = \frac{1}{x + 2}+2$ .找出函数f(f(x)) 的不连续点。

解决方案：

Here, $f[f(x)]=\frac{1}{\frac{1}{x+2}+2}=\frac{x+2}{2x+5}$

We observe that f(f( x )) is not defined at  x + 2 = 0 and 2x + 5 = 0.

If x + 2 = 0, then x = – 2 and if 2x + 5 = 0, then x = -5/2

Hence, the function is discontinuous at x = -5/2 and – 2.

问题 19. 找到函数f(t) = 的所有不连续点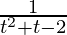$\frac{1}{t^2 + t - 2}$ , 其中 t = 1/(x – 1)。

解决方案：

Here, $f\left( t \right) = \frac{1}{t^2 + t - 2}$

 Now, let u = 1/(x – 1)

Therefore f( u ) = $\frac{1}{u^2 + 2u - u - 2}$

= $\frac{1}{\left( u + 2 \right)\left( u - 1 \right)}$

So, f (u ) is not defined at u = -2 and u = 1.

 If u = – 2, then -2 = 1/(x – 1)

⇒ 2x = 1

⇒ x = 1/2

 If u = 1, then 1 = 1/(x – 1)

⇒ x = 2

Hence, the function is discontinuous at x = 1/2 , 2.