问题11。平面穿过点(1 、、-2、5),并且垂直于将原点连接到点的线( 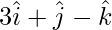 )。找到平面方程的向量和笛卡尔形式。
)。找到平面方程的向量和笛卡尔形式。
解决方案:
As we know that the vector equation of a plane passing through a point ![]() and normal to
and normal to ![]() is
is
![]() ….(i)
….(i)
Here, ![]()
![]()
![]() = Position vector of P – Position of vector of O
= Position vector of P – Position of vector of O
= ![]()
![]()
Now, put, all these values in equation (i), we get,
![]()
![]()
![]()
![]()
![]()
![]() ….(2)
….(2)
Now put ![]() in eq(2), we get
in eq(2), we get
![]()
(x)(3) + (y)(1) + (z)(−1) = -4
3x + y − z = -4
So, this is the required equation of plane.
问题12。找到将线段连接点(1、2、3)和(3、4、5)一分为二并且与之成直角的平面方程。
解决方案:
As we know that the vector equation of a plane passing through a point ![]() and normal to
and normal to ![]() is
is
![]() …..(i)
…..(i)
Here, ![]() = mid-point of AB
= mid-point of AB
So, ![]()
= Position vector of A + Position of vector of B/ 2
= ![]()
= ![]()
![]()
And, ![]()
![]() = Position vector of B – Position of vector of A
= Position vector of B – Position of vector of A
= ![]()
= ![]()
![]()
Now put all these values in eq(1), we get
![]()
![]()
![]()
![]()
![]() …..(2)
…..(2)
Now put ![]() in eq(2), we get
in eq(2), we get
![]()
(x)(2) + (y)(2) + (z)(2) = 18
2x + 2y + 2z = 18
or we can write as
x + y + z = 9
So, this is the required equation of plane.
问题13:证明以下几对平面的法线彼此垂直:
(i)x – y + z – 2 = 0和3x + 2y – z + 4 = 0
解决方案:
Given equations of planes are
x – y + z – 2 = 0 and 3x + 2y – z + 4 = 0
So first we solve, x – y + z – 2 = 0
![]()
![]() …..(i)
…..(i)
Now we solve, 3x + 2y – z =- 4
![]()
![]()
![]() …(ii)
…(ii)
So, from eq(i) and (ii), we conclude that
![]() is normal to eq(i) and
is normal to eq(i) and ![]() is normal to eq(ii)
is normal to eq(ii)
So,
![]() =
=![]()
= (1)(3) + (-1)(2) + (1)(-1)
=3 – 2 – 1
= 3 – 3 = 0
Hence,![]() is perpendicular to
is perpendicular to ![]()
(ii) 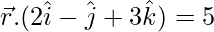 和
和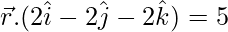
解决方案:
Given equations of planes are
![]() and
and ![]()
So first we solve, ![]()
![]()
![]() …..(1)
…..(1)
Now we solve, ![]()
![]()
![]() ……(2)
……(2)
So, from eq(i) and (ii), we conclude that
![]() is normal to eq(i) and
is normal to eq(i) and ![]() is normal to eq(ii)
is normal to eq(ii)
So,
![]() =
= ![]()
= (2)(2) + (-1)(-2) + (3)(-2)
= 4 + 2 – 6
= 6 – 6
= 0
Hence,![]() is perpendicular to
is perpendicular to ![]()
问题14:证明平面2x + 2y + 2z = 3的法线向量与坐标轴相等地倾斜。
解决方案:
Equation of plane = 2x + 2y + 2z = 3
So,
![]()
![]()
![]()
So, the normal to the plane ![]()
and the direction ratio of ![]()
So, the direction cosine of ![]() ….(1)
….(1)
![]() = √[(2)2 + (2)2 + (2)2]
= √[(2)2 + (2)2 + (2)2]
= √[4 + 4 + 4]
= √12 = 2√3
Now put the value of |\vec{n}| in eq(1), we get
Direction cosine of |\vec{n}| = ![]()
= ![]()
So, u = 1/√3, v = 1/√3, W = 1/√3
Let us assume that the α, β, γ be the angle that normal \vec{n} makes with the coordinate axes.
So, u = cos α = 1/√3
α = cos-11/√3 ….(2)
v = cos β = 1/√3
β = cos-11/√3 ….(3)
w = cos γ = 1/√3
γ = cos-11/√3 ….(4)
So, from equation (2), (3) and (4), we get
α = β = γ
Hence proved that the normal vector to the plane 2x + 2y + 2z = 3 is equally inclined with the coordinate axes.
问题15。找到一个垂直于平面12x – 3y + 4y = 1的大小为26个单位的向量。
解决方案:
Given that,
The equation of plane is = 12x – 3y + 4y = 1
and the magnitude = 26 units
So,
![]()
![]()
The normal to the plane is
![]()
![]() = √[(12)2 + (-3)2 + (4)2]
= √[(12)2 + (-3)2 + (4)2]
= √[144 + 9 + 16]
= √169 = 13
Hence, the unit vector ![]() =
= ![]()
![]()
Now we find a vector normal to the plane with magnitude
So,
26 = 26 ![]()
= 26 ![]()
= ![]()
So, this is the required vector
问题16.如果从(4,-1,2)绘制的线在点(-10,5,4)处以直角与平面相交,请找到该平面的方程。
解决方案:
As we know that the vector equation of a plane passing through a point ![]() and normal to
and normal to ![]() is
is
![]() …..(i)
…..(i)
Here, ![]() = position vector of B
= position vector of B
So, ![]()
and ![]()
![]() = Position vector of B – Position of vector of A
= Position vector of B – Position of vector of A
= ![]()
= ![]()
![]()
Now put all these values in eq(1), we get
![]()
![]()
![]()
![]()
![]() …..(2)
…..(2)
Now put ![]() in eq(2), we get
in eq(2), we get
![]()
(x)(-14) + (y)(6) + (z)(2) = 178
-14x + 6y + 3z = 178
Or we can write as
7x – 2y – z = -89
So, this is the required equation of plane.
问题17。找到平面方程,该平面将直角连接点(-1、2、3)和(3,-5、6)的线段一分为二。
解决方案:
Let assume that point (-1, 2, 3) is A point and point (3, -5, 6) is B point and C be the line mid-point of line segment AB
As we know that the vector equation of a plane passing through a point ![]() and normal to
and normal to ![]() is
is
![]() …(i)
…(i)
Here, ![]() = Position vector of C
= Position vector of C
So, ![]() [Because c is the mid point of line AB]
[Because c is the mid point of line AB]
![]()
![]()
![]()
Now, ![]()
![]() = Position vector of B- Position vector of A
= Position vector of B- Position vector of A
=![]()
= ![]()
= ![]()
![]()
Now put all these values in eq(1), we get
![]()
![]()
![]() = 28 ….(2)
= 28 ….(2)
Now put ![]() in eq(2), we get
in eq(2), we get
![]()
(x)(4) + (y)(-7) + (z)(3) = 28
4x – 7y + 3z = 28
So, this is the required equation of plane.
问题18。找到通过点(5,2,-4)并垂直于线径比为2、3,-1的平面的矢量和笛卡尔方程。
解决方案:
According to the given question
![]()
![]()
As we know that the vector equation of a plane passing through a point ![]() and normal to
and normal to ![]() is
is
![]()
So,
![]()
![]()
![]()
![]() ….(1)
….(1)
For cartesian equation:
Put ![]() in eq(1), we get
in eq(1), we get
![]()
(x)(2) + (y)(3) + (z)(-1) = 20
2x + 3y -z = 20
So, this is the required equation of plane.
问题19.如果O是原点,而P的坐标是(1、2,-3),则找到通过P并垂直于OP的平面的方程。
解决方案:
According to the question, a normal pass through point O(0, 0, 0) and P (1, 2, -3)
So, ![]()
and ![]()
As we know that the vector equation of a plane passing through a point ![]() and normal to
and normal to ![]() is
is
![]()
So,
![]()
![]()
![]()
![]()
For cartesian equation:
Put ![]() in eq(1), we get
in eq(1), we get
![]()
(x)(1) + (y)(2) + (z)(-3) = 14
x + 2y – 3z = 14
So, this is the required equation of plane.
问题20.如果O是原点,而A的坐标是(a,b,c)。求出OA的方向余弦,以及与OA成直角的A方向的平面方程。
解决方案:
According to the question it is given that, O is the origin and the coordinates of A are (a, b, c)
So, ![]()
Since, the direction ratios of OA are proportional to a, b, c
So, the direction cosines are:
![]()
So the equation of the line is,
![]()
ax + by + cz = a2 + b2 + c2