第12类RD Sharma解决方案–第29章飞机–练习29.12

问题1(i)：找到通过(5，1，6)和(3，4，1)的线与通过yz平面的线相交的点的坐标。

解决方案：

We know, the equation of line through the points (x₁,y₁,z₁) and (x₂,y₂,z₂) is $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

Therefore, equation of line joining (5, 1, 6) and (3, 4, 1) is $\frac{x-5}{3-5}=\frac{y-1}{4-1}=\frac{z-6}{1-6}$

⇒$\frac{x-5}{-2}=\frac{y-1}{3}=\frac{z-6}{-5}$

Let, $\frac{x-5}{-2}=\frac{y-1}{3}=\frac{z-6}{-5}=\lambda$, where $\lambda$ is a constant.

⇒ $x=-2\lambda+5, y=3\lambda+1, z=-5\lambda+6$

Coordinates of any point on the line is in the form of $(-2\lambda+5,3\lambda+1,-5\lambda+6)$

Since, the line crosses the yz-plane, the point $(-2\lambda+5,3\lambda+1,-5\lambda+6)$ must satisfy the equation of plane x=0,

⇒$-2\lambda+5=0$ ⇒ $\lambda=\frac{5}{2}$ 

Therefore, coordinates of points is given by, putting $\lambda=\frac{5}{2}$ we get,

⇒ $(0,\frac{17}{2},\frac{13}{2})$

(ii)找到通过(5，1，6)和(3，4，1)的线与通过zx平面的线相交的点的坐标。

解决方案：

We know, the equation of line through the points (x1,y1,z1) and (x2,y2,z2) is $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

Therefore, equation of line joining (5, 1, 6) and (3, 4, 1) is$\frac{x-5}{3-5}=\frac{y-1}{4-1}=\frac{z-6}{1-6}$

⇒$\frac{x-5}{-2}=\frac{y-1}{3}=\frac{z-6}{-5}$

Let, $\frac{x-5}{-2}=\frac{y-1}{3}=\frac{z-6}{-5}=\lambda$ ,where $\lambda$ is a constant.

⇒ $x=-2\lambda+5, y=3\lambda+1, z=-5\lambda+6$

Coordinates of any point on the line is in the form of $(-2\lambda+5,3\lambda+1,-5\lambda+6)$

Since, the line crosses the zx-plane, the point $(-2\lambda+5,3\lambda+1,-5\lambda+6)$ must satisfy the equation of plane y=0,

⇒ $3\lambda+1=0$ ⇒ $\lambda=\frac{-1}{3}$

Therefore, the coordinates of point is given by, putting $\lambda=\frac{-1}{3}$ we get,

⇒ $(\frac{17}{3},0,\frac{23}{3})$

问题2：找到通过(3，-4，-5)和(2，-3，1)的线与平面2x + y + z = 7相交的点的坐标。

解决方案：

We know, the equation of line through the points (x1,y1,z1) and (x2,y2,z2) is $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

Therefore, line joining the points (3, -4, -5) and (2, -3, 1) is $\frac{x-3}{2-3}=\frac{y+4}{-3+4}=\frac{z+5}{1+5}$

⇒ $\frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}$

Let $\frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}=\lambda$ where $\lambda$ is constant.

⇒ $x=-\lambda+3,y=\lambda-4,z=6\lambda-5$

The coordinates of any point on the line is given by $(-\lambda+3,\lambda-4,6\lambda-5)$

The line crosses the plane, therefore, point must satisfy the plane equation.

$2(-\lambda+3)+\lambda-4+6\lambda-5=7$

⇒ $\lambda=2$

Therefore, The coordinates of point are given by, putting $\lambda=2$,

⇒ $(-2+3, 2-4, 6(2)-5)$ 

⇒ (1, -2, 7)

问题3：找到线的交点到点(-1，-5，-10)的距离

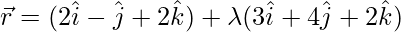 $\vec{r}=(2\hat{i}-\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})$和飞机$\vec{r}.(\hat{i}-\hat{j}+\hat{k})=5.$

解决方案：

Given equation of line is $\vec{r}=(2\hat{i}-\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})$

⇒ $\vec{r}=(2+3\lambda)\hat{i}+(-1+4\lambda)\hat{j}+(2+2\lambda)\hat{k}$

Coordinates of any point of line should be in the form of $(2+3\lambda,-1+4\lambda,2+2\lambda)$

We know, the intersection point of line and plane lies on the plane, using this,

⇒ $[(2+3\lambda)\hat{i}+(-1+4\lambda)\hat{j}+(2+2\lambda)\hat{k}].(\hat{i}-\hat{j}+\hat{k})=5.$

⇒ $2+3\lambda+1+4\lambda+2+2\lambda-5=0$

⇒ $\lambda=0$

Therefore, coordinates of point is given by, putting $\lambda=0$ ,

⇒ (2, -1, 2)

Therefore, now distance between (-1, -5, -10) and (2, -1, 2) is,

⇒ $\sqrt{(-1-2)^2+(-5+1)^2+(-10-2)^2}$

⇒ $\sqrt{9+16+144}$ ⇒ 13 units

问题4：找到点(2、12、5)与直线相交点的距离

 $\vec{r}=(2\hat{i}-4\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})$和$\vec{r}.(\hat{i}-2\hat{j}+\hat{k})=0.$

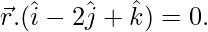
解决方案：

Given equation of line is $\vec{r}=(2\hat{i}-4\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})$

⇒ $\vec{r}=(2+3\lambda)\hat{i}+(-4+4\lambda)\hat{j}+(2+2\lambda)\hat{k}$

Coordinates of any point of line should be in the form of $(2+3\lambda,-4+4\lambda,2+2\lambda)$

We know, the intersection point of line and plane lies on the plane, using this,

⇒ $[(2+3\lambda)\hat{i}+(-4+4\lambda)\hat{j}+(2+2\lambda)\hat{k}].(\hat{i}-2\hat{j}+\hat{k})=0$.

⇒ $2+3\lambda+8-8\lambda+2+2\lambda=0$

⇒ $\lambda=-4$

Therefore, coordinates of point is given by, putting $\lambda=-4$,

⇒ (14, 12, 10).

Therefore, now distance between the points (2, 12, 5) and (14, 12, 10) is,

⇒ $\sqrt{(14-2)^2+(12-12)^2+(10-5)^2}$ 

⇒ $\sqrt{144+0+25}$ ⇒ 13 units

问题5：找到从连接点A(2，-1，2)和B(5，3，4)与平面x-y相交的点(-1，-5，-10)的距离+ z = 5。

解决方案：

Equation of line joining the points A(2, -1, 2) and B(5, 3, 4) is $\frac{x-2}{5-2}=\frac{y-(-1)}{3-(-1)}=\frac{z-2}{4-2}$

⇒ $\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{2}$

Let, $\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{2}=\lambda$

⇒ $x=3\lambda+2,y=4\lambda-1,z=2\lambda+2$

Coordinates of any point on the line is given by $(3\lambda+2,4\lambda-1,2\lambda+2)$

We know, The intersection of line and plane lies on the plane, so,

⇒ $3\lambda+2-(4\lambda-1)+2\lambda+2=5$

⇒ $\lambda=0$

Therefore, the coordinates of points is, putting $\lambda=0$

⇒ (2, -1, 2)

Now, the distance between the points (-1, -5, -10) and (2, -1, 2) is,

⇒ $\sqrt{(2+1)^2+(-1+5)^2+(2+10)^2}$

⇒ $\sqrt{9+16+144}$ ⇒ 13 units

问题6：求点(3，4，4)距该点的距离，在该点处连接点A(3，-4，-5)和B(2，-3，1)的线与2x + y相交+ z = 7。

解决方案：

Equation of line passing through A(3, -4, -5) and B(2, -3, 1) is given by $\frac{x-3}{2-3}=\frac{y-(-4)}{-3-(-4)}=\frac{z-(-5)}{1-(-5)}$

⇒ $\frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}$

Let $\frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}=\lambda$

⇒ $x=-\lambda+3,y=\lambda-4,z=6\lambda-5$

Coordinates of any point on the line is given by $(-\lambda+3,\lambda-4,6\lambda-5)$

We know, The intersection of line and plane lies on the plane, so,

⇒ $2(-\lambda+3)+(\lambda-4)+(6\lambda-5)=7$

⇒ $5\lambda-3=7$

⇒ $\lambda=2$

Therefore, the coordinates of points is, putting $\lambda=2$

⇒ (1, -2, 7)

Now, the distance between (3, 4, 4) and (1, -2, 7) is,

⇒ $\sqrt{(3-1)^2+(4+2)^2+(4-7)^2}$

⇒ $\sqrt{4+36+9}$ = 7 units

问题7：找到沿平面x = y = z测得的点(1，-5，9)与平面x- y + z = 5的距离。

解决方案：

Given, The equation of line is x=y=z, it can also be written as,

$\frac{x-0}{1}=\frac{y-0}{1}=\frac{z-0}{1}$, where (1, 1, 1) are direction ratios of the line.

Here we have to measure the distance along the line, the equation of line parallel to x=y=z have same direction ratios (1, 1, 1),

So, the equation of line passing through (1, -5, 9) and having direction ratios (1, 1, 1) is,

⇒ $\frac{x-1}{1}=\frac{y+5}{1}=\frac{z-9}{1}$

Let $\frac{x-1}{1}=\frac{y+5}{1}=\frac{z-9}{1}=\lambda$

Coordinates of any point on the line is given by $(\lambda+1,\lambda-5,\lambda+9)$

We know, The intersection of line and plane lies on the plane, so,

⇒ $(\lambda+1)-(\lambda-5)+(\lambda+9)=5$

⇒ $\lambda=-10$

Therefore, the coordinates of point is given by, putting $\lambda=-10$ = (-9, -15, -1)

Now, distance between the points (1, -5, 9) and (-9, -15, -1) is,

⇒ $\sqrt{(1+9)^2+(-5+15)^2+(9+1)^2}$

⇒ $\sqrt{300}$ units.