第 12 类 RD Sharma 解决方案 - 第 29 章飞机 - 练习 29.15 |设置 2
问题 8. 求平面 2x – y + z + 3 = 0 中点 (1, 3, 4) 的图像。
解决方案:
According to the question we have to find the image of point P(1, 3, 4)
in the plane 2x – y + z +3 = 0
Now let us assume that Q be the image of the point.
Here, the direction ratios of normal to plane = 2, -1, 1
The direction ratios of PQ which is parallel to the normal to the plane
is proportional to 2, -1, 1 and the line PQ is passing through point P(1, 3, 4).
Thus, equation of the line PQ is:
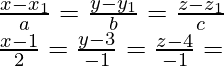
Now, the general point on the line PQ = (2λ + 1, -λ + 3, λ + 4)
Let Q = (2λ + 1, -λ + 3, λ + 4) -Equation(1)
Here, Q is the image of P, so R is the mid point of PQ
Coordinates of R = 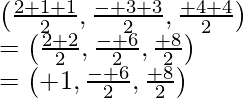
Point R is lies on the plane 2x – y + z + 3 = 0
= 2(λ + 1) – ![]()
4λ + 4 + λ – 6 + λ + 8 + 6 = 0
6λ = -12
λ = -2
Now, put the value of λ in equation(1), we get
= (-4 + 1, 2 + 3, -2 + 4)
= (-3, 5, 2)
Hence, the image of point P(1, 3, 4) is (-3, 5, 2)
问题9.用位置向量求点的距离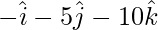 从线的交点
从线的交点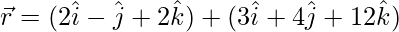 与飞机
与飞机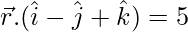 .
.
解决方案:
According to the question we have to find distance of a point A with position
vector ![]() from the point of intersection of
from the point of intersection of
line ![]()
with plane ![]()
Let the point of intersection of line and plan be ![]()
The line and the plane will intersect when,
=5\\ [(2+3λ)\hat{i}+(-1+4λ)\hat{j}+(2+12λ)\hat{k}](\hat{i}-\hat{j}+\hat{k})=5\\](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions-_Chapter_29_The_Plane_%E2%80%93_Exercise_29.15_%7C_Set_2_10.jpg)
(2 + 3λ)(1) + (-1 + 4λ)(-1) + (2 + 12λ)(1) = 5
2 + 3λ + 1 – 4λ + 2 + 12λ = 5
11λ = 5 – 5
λ = 0
So, the point B is given by
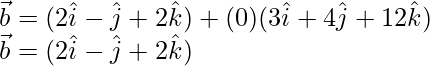
![]()
![]()
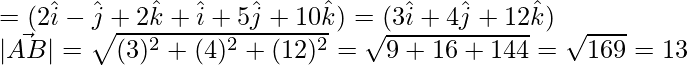
The required distance is 13 units.
问题 10. 求点 (1, 1, 2) 到平面的垂线的长度和底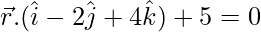 .
.
解决方案:
Plane = x – 2y + 4z + 5 = 0 -Equation(1)
Point = (1, 1, 2)
D = ![]()
= 12/√21
The length of the perpendicular from the given point to the plane = 12/√21
Let us assume that the foot of perpendicular be (x, y, z).
So DR’s are in proportional
![]()
x = k + 1
y = -2k + 1
z = 4k + 2
Substitute (x, y, z) = (k + 1, -2k + 1, 4k + 2) in the plane equation(1)
k + 1 + 4k – 2 + 16k + 8 + 5 = 0
21k = -12
k = -12/21 = -4/7
Hence, the coordinate of the foot of the perpendicular = (3/7, 15/7, -2/7)
问题 11. 求垂线脚的坐标和点 P(3, 2, 1) 到平面 2x – y + z + 1 = 0 的垂线距离。同时求该点在平面上的像.
解决方案:
Given:
Plane = 2x – y + z + 1 = 0 -Equation(1)
Point P = (3, 2, 1)
D =![]()
The perpendicular distance of the point P from the plane(D) = √6
Let us assume that the foot of perpendicular be (x, y, z).
So DR’s are in proportional
![]()
x = 2k + 3
y = -k + 2
z = k + 1
Substitute (x, y, z) = (2k + 3, -k + 2, k + 1) in the plane equation(1)
4k + 6 + k – 2 + k + 1 + 1 = 0
6k = -6
k = -6/6 = -1
The coordinate of the foot of the perpendicular = (1, 3, 0)
问题12.求垂直于平面的单位向量的方向余弦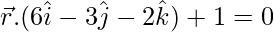 穿越原点。
穿越原点。
解决方案:
Given:
Equation of the plane ![]()
Thus, the direction ratios normal to the plane are 6, -3 and -2
Hence, the direction cosines to the normal to the plane are
= ![]()
= 6/7, -3/7, -2/7
= -6/7, 3/7, 2/7
The direction cosines of the unit vector perpendicular to the plane
are same as the direction cosines of the unit vector perpendicular
to the plane are: -6/7, 3/7, 2/7
问题 13. 求从原点到平面 2x – 3y + 4z – 6 = 0 的垂线的底坐标。
解决方案:
According to the question,
Plane = 2x – 3y + 4z – 6 = 0
The direction ratios of the normal to the plane are 2, -3 and 4.
Thus, the direction ratios of the line perpendicular to the plane are 2, -3 and 4.
The equation of the line passing (x1, y1, z1) having direction ratios a, b and c is
![]()
Thus, the equation of the line passing through the origin
with direction ratios 2, -3 and 4 is
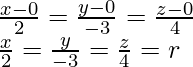
Here, r is same constant.
Any point on the line is of the form 2r, -3r, and 4r,
if the point P(2r, -3r, 4r) lies on the plane 2x – 3y + 4z – 6 = 0.
Thus, we have,
2(2r) – 3(-3r) + 4(4r) – 6 = 0
4r + 9r + 16r – 6 = 0
29r = 6
r = 6/29
Thus, the coordinates of the point of intersection of the perpendicular
from the origin and the plane are:
P(2×6/29, -3×629, 4×6/29) = P(12/29, -18/29, 24/29)
问题 14. 求点 (1, 3/2, 2) 到平面 2x – 2y + 4z +5 = 0 的垂线的长度和底。
解决方案:
Given:
Point = (1, 3/2, 2)
Plane = 2x – 2y + 4z + 5 = 0
D = ![]()
= √6
So, the length of the perpendicular from the point to the plane(D) = √6
Let the foot of perpendicular be (x, y, z). So, DR’s are in proportional
![]()
x = 2k + 1
y = -2k + 3/2
z = 4k + 2
So, using the values of x, y, z in equation of the plane we have,
2(2k + 1) – 2(-2k + 2/3) +4(4k + 2) + 5 = 0
4k + 2 + 4k – 3 + 16k + 8 + 5 = 0
24k = -12
k = -1/2
So, the coordinate of the foot of the perpendicular = (0, 5/2, 0)