问题1.找到平行平面2x – y + 3z – 4 = 0和6x – 3y + 9z + 13 = 0之间的距离
解决方案:
Let P(x1, y1, z1) be any point on plane 2x – y + 3z – 4 = 0.
⟹ 2x1 – y1 + 3z1 = 4 (equation-1)
Distance between (x1, y1, z1) and the plane
6x – 3y + 9z + 13 = 0:
As we know that, the distance of point (x1, y1, z1) from the plane π: ax + by + cz + d = 0 is given by:
p = ![]()
Now, substitute the values, we get
p = 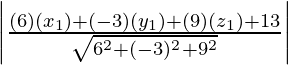
= 
= ![]() [by using equation 1]
[by using equation 1]
= ![]()
Therefore, the distance between the parallel planes 2x – y + 3z – 4 = 0 and 6x – 3y + 9z + 13 = 0 is ![]() units.
units.
问题2。找到经过点(3,4,-1)并与2x – 3y + 5z + 7 = 0平面平行的平面的方程。还要找到两个平面之间的距离。
解决方案:
Since the plane is parallel to 2x – 3y + 5z + 7 = 0, it must be of the form:
2x – 3y + 5z + θ = 0
It is given that,
The plane passes through (3, 4, –1)
⟹ 2(3) – 3(4) +5(–1) + θ = 0
θ = -11
Thus,
The equation of the plane is as follows:
2x – 3y + 5z – 11 = 0
Distance of the plane 2x – 3y + 5z + 7 = 0 from (3, 4, –1):
As we know that, the distance of point (x1, y1, z1) from the plane π: ax + by + cz + d = 0 is given by:
p = ![]()
Now, after substituting the values, we will get
= 
= ![]()
Therefore, the distance of the plane 2x – 3y + 5z + 7 = 0 from (3, 4, -1) is ![]()
问题3.找到与平面2x – 2y + z + 3 = 0和2x – 2y + z + 9 = 0平行的平面的方程
解决方案:
Given:
Equation of planes:
π1= 2x – 2y + z + 3 = 0
π2= 2x – 2y + z + 9 = 0
Let the equation of the plane mid–parallel to these planes be:
π3: 2x – 2y + z + θ = 0
Now,
Let P(x1, y1, z1) be any point on this plane,
⟹ 2(x1) – 2(y1) + (z1) + θ = 0 —(equation-1)
As we know that, the distance of point (x1, y1, z1) from the plane π: ax + by + cz + d = 0 is given by:
p = ![]()
Distance of P from π1:
p = 
= ![]() (By using equation 1)
(By using equation 1)
Similarly,
DIstance of q from π2:
q = 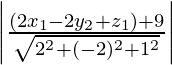
= ![]() (By using equation 1)
(By using equation 1)
As π3 is mid-parallel is π1 and π2:
p = q
So,
![]()
Now square on both sides, we get
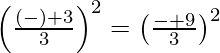
(3 – θ)2 = (9 – θ)2
9 – 2×3×θ + θ2 = 81 – 2×9×θ + θ2
θ = 6
Now, substitute the value of θ = 6 in equation 2x – 2y + z + θ = 0, we get
Hence, the equation of the mid-parallel plane is 2x – 2y + z + 6 = 0
问题4.找出平面之间的距离 和
和
解决方案:
Let ![]() be the position vector of any pont P on the plane
be the position vector of any pont P on the plane
![]()
So,
![]() —(equation 1)
—(equation 1)
As we know that, the distance of from ![]() the plane
the plane ![]() is given by:
is given by:
p = ![]()
Length of perpendicular from![]() is given by substituting the values of
is given by substituting the values of![]() , we get
, we get
p = 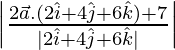
= ![]()
= ![]()
p = ![]()
Therefore, the distance between the planes
![]() and
and ![]() is
is ![]()