第 12 类 RD Sharma 解决方案 – 第 29 章飞机 – 练习 29.4

问题 1. 求距原点 3 个单位且有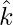$\hat{k}$作为垂直于它的单位向量。

解决方案：

We know, the vector equation of a plane normal to unit vector$\hat{n}$and at a distance of d from origin is given as

$\vec{r}.\hat{n} = d$

Here, d = 3 units ,we get

$\vec{r}.\hat{k} = 3$

问题 2. 求距原点 5 个单位且垂直于向量的平面的向量方程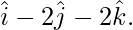$\hat{i} - 2\hat{j} - 2\hat{k}.$

解决方案：

We know, the vector equation of a plane normal to unit vector$\hat{n}$and at a distance of d from origin is given as

$\vec{r}.\hat{n} = d$

Here, d = 5 units

and$\vec{n} = \hat{i} - 2\hat{j} - 2\hat{k}.$

$\hat{n} = \frac{\vec{n}}{\vec{|n|}}$

$= \frac{\hat{i} - 2\hat{j} - 2\hat{k}}{\sqrt{1^2 + (-2)^2 + (-2)^2}}$

$= \frac{\hat{i} - 2\hat{j} - 2\hat{k}}{\sqrt{9}}$

$= \frac{\hat{i} - 2\hat{j} - 2\hat{k}}{3}$

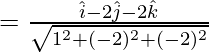
Hence the required equation is,

$\vec{r}.\frac{1}{3}(\hat{i} - 2\hat{j} - 2\hat{k}) = 5$

问题 3. 将方程 2x – 3y – 6z = 14 化简为范式，从而求出从原点到平面的垂线长度。另外，求平面法线的余弦方向。

解决方案：

$(x\hat{i} + y\hat{j} + z\hat{k}).(2\hat{i} - 3\hat{j} - 6\hat{k}) = 14$

Dividing the equation by$\sqrt{2^2 + (- 3)^2 + (- 6)^2}$

$\vec{r}.\frac{(2\hat{i}- 3\hat{j} - 6\hat{k})}{\sqrt{4 + 9 + 36}} = \frac{14}{\sqrt{4 + 9 + 36}}$

$⇒ \vec{r}.[\frac{2}{7}\hat{i} - \frac{3}{7}\hat{j} - \frac{6}{7}\hat{k}] = 2$……(1)

Since Vector equation of a plane with distance d and normal to the unit vector n is given by

$\vec{r}.\hat{n} = d$……(2)

Comparing (1) and (2), we get

Distance from origin = 2 units

Direction cosine of normal to plane =$\frac{2}{7}, - \frac{3}{7}, \frac{6}{7}$

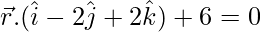问题 4. 化简方程$\vec{r}.(\hat{i} - 2\hat{j} + 2\hat{k}) + 6 = 0$到正常形式，因此找到从原点到平面的垂直长度。

解决方案：

$Given: \vec{r}.(\hat{i} - 2\hat{j} + 2\hat{k}) = -6$

Multiplying both sides by –1, we get

$\vec{r}.(\hat{-i} + 2\hat{j} - 2\hat{k}) = 6$

$⇒ \vec{r}.\vec{n} = 6$…..(1)

$|\vec{n}| = \sqrt{(-1)^2 + 2^2 + (-2)^2} = 3$

Dividing (1) by 3 on both sides,

$\vec{r}.[-\frac{\hat{i}}{3} + \frac{2}{3}\hat{j} - \frac{2}{3}\hat{k}] = 2$

Since vector equation of a plane with distance d and normal to the unit vector n is given by

$\vec{r}.\hat{n} = d$……(2)

Comparing (1) and (2), we get

d = 2

$\hat{n} = [-\frac{\hat{i}}{3} + \frac{2}{3}\hat{j} - \frac{2}{3}\hat{k}]$

Length of normal = 2 units.

问题 5. 写出方程 2x – 3y + 6z + 14 = 0 的范式。

解决方案：

$(x\hat{i} + y\hat{j} + z\hat{k}).(2\hat{i} - 3\hat{j} + 6\hat{k}) = -14$

$⇒ \hat{r}.(2\hat{i} - 3\hat{j} + 6\hat{k}) = -14$

Multiplying both sides by –1, we get

$\vec{r}.(-2\hat{i} + 3\hat{j} - 6\hat{k}) = 14$

$⇒ \vec{r}.\vec{n} = 14$…..(1)

$|\vec{n}| = \sqrt{(-2)^2 + 3^2 + (-6)^2} = 7$

Dividing (1) by 7 on both sides,

$\vec{r}.[-\frac{2}{3}\hat{i} + \frac{3}{7}\hat{j} - \frac{6}{7}\hat{k}] = 2$

Hence normal form of the equation is

$-\frac{2}{7}x + \frac{3}{7}y - \frac{6}{7}z = 2$

问题 6. 原点到平面的垂线方向比为 12,–3,4，垂线长度为 5。求平面方程。

解决方案：

Normal vector =$\vec{n} = 12\hat{i} - 3\hat{j} + 4\hat{k}$

$|\vec{n}| = \sqrt{(12)^2 + (-3)^2 + (4)^2} = \sqrt{169} = 13$

So, Normal unit vector$= \hat{n} = \frac{\vec{n}}{ |\vec{n}|}$

$= \frac{12}{13}\hat{i} - \frac{3}{13}\hat{j} + \frac{4}{13}\hat{k} = 5$

Since vector equation of a plane with distance d and normal to the unit vector n is given by

$\vec{r}.\hat{n} = d$

$⇒ \vec{r}.[\frac{12}{13}\hat{i} - \frac{3}{13}\hat{j} + \frac{4}{13}\hat{k}] = 5$

or,$\frac{12}{13}x - \frac{3}{13}y + \frac{4}{13}z = 5$

问题 7. 求平面 x + 2y + 3z – 6 = 0 的单位法向量。

解决方案：

$(x\hat{i} + y\hat{j} + z\hat{k}).(\hat{i} + 2\hat{j} + 3\hat{k}) = 6$

$⇒ \hat{r}.(\hat{i} + 2\hat{j} + 3\hat{k}) = 6$

$⇒ \vec{r}.\vec{n} = 6$…….(1)

$|\vec{n}| = \sqrt{(1)^2 + 2^2 + (3)^2} = \sqrt{14}$

Dividing (1) by$\sqrt{14}$, we get

$\vec{r}.[\frac{1}{\sqrt14}\hat{i} + \frac{2}{\sqrt14}\hat{j} + \frac{3}{\sqrt14}\hat{k}] = \frac{6}{\sqrt14}$

Since vector equation of a plane with distance d and normal to the unit vector n is given by

$\vec{r}.\hat{n} = d$…..(2)

Thus, normal unit vector =$\hat{n} = \frac{1}{\sqrt14}\hat{i} + \frac{2}{\sqrt14}\hat{j} + \frac{3}{\sqrt14}\hat{k}$

问题 8. 求距离为 的平面方程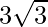$3\sqrt{3}$从原点和法线到与坐标轴相同倾斜的单位。

解决方案：

Since vector equation of a plane with distance d and normal to the unit vector n is given by

$\vec{r}.\hat{n} = d$

d =$3\sqrt{3} units$

Let$\vec{a}$be a normal vector,$\vec{a} = p\hat{i} + q\hat{j} + r\hat{k}$

Since$\vec{a}$is equally inclined to the coordinate axes, let l, m, n be the cosines of$\vec{n}$. Also l = m = n.

We know, l² + m² + n² = 1

or,$l = m = n = \frac{1}{\sqrt{3}}$

Now,$\hat{a} = \frac{\hat{i}}{\sqrt{3}} + \frac{\hat{j}}{\sqrt{3}} + \frac{\hat{k}}{\sqrt{3}}$

Vector equation of the required plane is

$\vec{r}.\frac{1}{\sqrt3}[\hat{i} + \hat{j} + \hat{k}] = 3\sqrt{3}$

or,$\vec{r}(\hat{i} + \hat{j} + \hat{k}) = 9$

or, x + y + z = 9.

问题 9. 求通过点 (1,2,1) 并垂直于连接点 (1,4,2) 和 (2,3,5) 的直线的平面方程。还要找到原点到平面的垂直距离。

解决方案：

Vector equation of a plane is given by

$(\vec{r} - \vec{a}).\vec{n} = 0$…..(1)

We have,$\vec{a} = \hat{i} - 2\hat{j} + \hat{k}$

and,$\vec{n} = \vec{BC} = \hat{i} - \hat{j} + 3\hat{k}$

Putting$\vec{a}$and$\vec{n}$in (1), we get

$\vec{r}(\hat{i} - \hat{j} + 3\hat{k}) = 2$….(2)

$|\vec{n}| = \sqrt{(1)^2 + 1^2 + (3)^2} = \sqrt{11}$

Dividing (1) by$\sqrt{11}$

$\vec{r}.[\frac{1}{\sqrt11}\hat{i} - \frac{1}{\sqrt11}\hat{j} + \frac{3}{\sqrt11}\hat{k}] = \frac{2}{\sqrt11}$

Hence, vector equation of plane is$\vec{r}.(\hat{i} - \hat{j} + 3\hat{k}) = 2.$

and, cartesian form is x – y + 3z – 2 = 0.

问题 10. 求距离为 的平面的矢量方程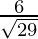$\frac{6}{\sqrt{29}}$从原点和它从原点的法向量是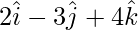$2\hat{i} - 3\hat{j} + 4\hat{k}$ .此外，找到它的笛卡尔形式。

解决方案：

Since vector equation of a plane with distance d and normal to the unit vector n is given by

$\vec{r}.\hat{n} = d$

Since,$|\vec{n}| = \sqrt{(2)^2 + (-3)^2 + (4)^2} = \sqrt{29}$

Unit vector normal to the plane =$\frac{\vec{n}}{|\vec{n}|}$

or,$\hat{n} = \frac{2}{\sqrt29}\hat{i} - \frac{3}{\sqrt29}\hat{j} + \frac{4}{\sqrt29}\hat{k}$

$d = \frac{6}{\sqrt29}$

Vector equation becomes,

$\vec{r}.[\frac{2}{\sqrt29}\hat{i} - \frac{3}{\sqrt29}\hat{j} + \frac{4}{\sqrt29}\hat{k}] = \frac{6}{\sqrt29}$

Cartesian equation is 2x – 3y + 4z = 6.

问题 11. 求平面 2x – 3y + 4z – 6 = 0 到原点的距离。

解决方案：

2x – 3y + 4z – 6 = 0

or, 2x – 3y + 4z = 6

Vector equation becomes,

$(x\hat{i} + y\hat{j} + z\hat{k}).(2\hat{i} - 3\hat{j} + 4\hat{k}) = 6$

or,$\vec{r}.(2\hat{i} - 3\hat{j} + 4\hat{k}) = 6$…..(1)

$|\vec{n}| = \sqrt{(2)^2 + (-3)^2 + (4)^2} = \sqrt{29}$

Dividing (1) by$|\vec{n}|$, normal form of equation becomes,

$\vec{r}.[\frac{2}{\sqrt29}\hat{i} - \frac{3}{\sqrt29}\hat{j} + \frac{4}{\sqrt29}\hat{k}] = \frac{6}{\sqrt29}$

Hence, the perpendicular distance of the origin from the plane is$\frac{6}{\sqrt29}$units.