第 12 类 RD Sharma 解决方案 - 第 29 章飞机 - 练习 29.11 |设置 1
问题1.求直线之间的角度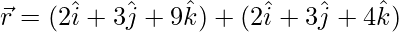 和飞机
和飞机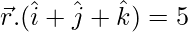 .
.
解决方案:
Given that, the line is ![]() and the plane is
and the plane is ![]() .
.
So,
As we know that the angle between a line and a plane is
![]()
So,
⇒ ![]()
⇒ 9/√87
问题 2. 求直线之间的夹角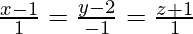 平面 2x + y – z = 4。
平面 2x + y – z = 4。
解决方案:
The given line ![]() is parallel to the vector
is parallel to the vector ![]() and the plane 2x + y – z = 4 is normal to the vector
and the plane 2x + y – z = 4 is normal to the vector ![]() .
.
So, the angle between line and plane is
![]()
= ![]()
= 0
问题 3. 求连接点 (3, -4, -2) 和 (12, 2, 0) 的线与平面 3x – y + z = 1 之间的角度。
解决方案:
According to the question, the line passes through A(3,- 4,- 2) and B(12, 2, 0).
So, ![]()
= ![]()
= ![]()
So, the line is parallel to the vector ![]() and the plane is normal to the vector
and the plane is normal to the vector ![]()
So, the angle between the line and the plane is,
![]()
= ![]()
= ![]()
Thus, ![]() .
.
问题 4. 线路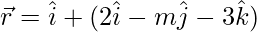 平行于平面
平行于平面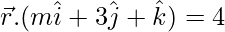 .找米。
.找米。
解决方案:
Give that the equation of line is ![]() and the equation of plane is
and the equation of plane is ![]()
So, ![]()
![]()
If a line is parallel to a plane, then the normal to the plane is perpendicular to the line.
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ 2m – 3m – 3 = 0
⇒ – m – 3 = 0
⇒ m = –3
问题 5. 证明向量方程为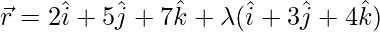 平行于其矢量的平面
平行于其矢量的平面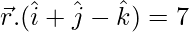 .另外,找出它们之间的距离。
.另外,找出它们之间的距离。
解决方案:
Given that the plane passes through the point with the position vector ![]() and is parallel to the vector
and is parallel to the vector ![]() .
.
So, the normal vector ![]() and d = 7 .
and d = 7 .
![]()
= 1 + 3 – 4
= 4 – 4
= 0
As we know that ![]() is perpendicular to
is perpendicular to ![]()
So, the distance between the line and plane is
![]()
= 7/√3units.
问题 6. 求通过原点垂直于平面的直线的矢量方程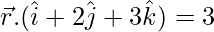 .
.
解决方案:
Given that the line is perpendicular to the plane ![]()
So, the line is parallel to the normal .
As we know that the equation of a line is pass through ![]() and parallel to
and parallel to ![]() is
is ![]()
⇒ ![]()
⇒ ![]()
问题 7. 求平面通过 (2, 3, -4) 和 (1, -1, 3) 并平行于 x 轴的方程。
解决方案:
Given that the equation of the plane through point (2, 3, -4) is
a(x − 2) + b(y − 3)+c(z + 4) = 0 …(1)
Since this plane passes through point (1, -1, 3).
⇒ a(1 − 2) + b( −1 − 3) + c( 3 + 4) = 0
⇒ − a − 4b + 7c = 0 …(2)
Equation(1) is parallel to x-axis and is perpendicular to the yz-plane whose equation is x = 0 or 1 . x + 0 . y + 0 . z = 0
⇒ a(1) + b(0) + c(0) = 0 …(3)
One solving eq(1), (2), and (3), we get
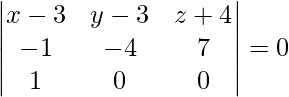
⇒ 7y + 4z – 5 = 0 is the required equation.
问题 8. 求通过点 (0, 0, 0) 和 (3, -1, 2) 并平行于直线的平面方程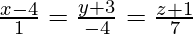
解决方案:
Given that the plane pass through point(0, 0, 0), so the equation of the plane is a(x − 0) + b(y − 0)+c(z + 0) = 0.
⇒ ax + by + cz = 0 …(1)
and the same plane passes through point (3, -1, 2). So, the equation of the plane is
3a – b + 2c = 0 …(2)
Equation(1) is parallel to the given line so,
a(1) + b(-4) + c (7) = 0 …(3)
On solving eq(1), (2), and (3), we get
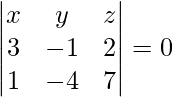
⇒ x – 19y – 11z = 0
Hence, the required equation of the plane is x – 19y – 11z = 0
问题 9. 求通过 (1, 2, 3) 并平行于平面的直线的向量和笛卡尔方程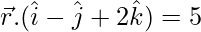 和
和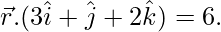
解决方案:
Given that the equation of the line passing through (1, 2, 3) is
![]() …(1)
…(1)
Here, the given line is parallel to plane x – y + 2z = 5
So, a × 1 + b × – 1 + c × 2 = 0
⇒ a – b + 2c = 0 …(3)
Also, the given line is parallel to plane 3x + y + z = 6
So, a × 3 + b × 1 + c × 1 = 0
⇒ 3a + b + c = 0 …(4)
On solving the equation (3) and (4) we get,
⇒ ![]()
∴ a = – 3k, b = 5k and c = 4k
Now, put the value in the equation(1), we get
![]()
Now, multiplying by k we get
The required equation is ![]()
⇒ ![]()
Hence, the equation of the plane is ![]()
问题 10. 证明平面 5x + 2y – 4z + 2 = 0 和 2x + 8y + 2z – 1 = 0 的截面线平行于平面 4x – 2y – 5z – 2 = 0。
解决方案:
Let us consider a, b and c be the direction ratios.
So,
⇒ a + 4b + c = 0
and, 5a + 2b – 4c = 0
On solving the above two equations, we get
![]()
⇒ ![]()
As we know that the line ![]() is parallel to plan a2x + b2y + c2z + d2 = 0, when a1a2 + b1b2 + c1c2 = 0
is parallel to plan a2x + b2y + c2z + d2 = 0, when a1a2 + b1b2 + c1c2 = 0
So, the line with direction ratio(a, b, c) is parallel to plane 4x – 2y – 5z – 2 = 0
aa1 + bb1 + cc1 = 0
2(4) + (-1)(-2) + (2)(-5) = 0
Hence proved that the line of section of the given plane is parallel to the given plane.
问题 11. 求通过点 (1, -1, 2) 并垂直于平面 2x – y + 3z – 5 = 0 的直线的向量方程。
解决方案:
Let us consider a, b and c be the direction ratios.
Given that the equation of the line passing through the point (1, -1, 2)
So,
![]() …..(1)
…..(1)
Also, the line is parallel to the normal of the plane.
⇒ ![]()
⇒ a = 2λ, b = -λ , c = 3λ
Now put all these values in eq(1), we get
![]()
So, the line passes through a point whose position vector is ![]() and parallel to
and parallel to ![]()
So, ![]()
⇒ ![]() is the required equation.
is the required equation.
问题 12. 求通过点 (2, 2, -1) 和 (3, 4, 2) 并平行于方向比为 7, 0, 6 的直线的平面方程。
解决方案:
Given that the equation of the plane through the point (2, 2, -1)
a(x – 2) + b(y – 2) + c(z + 1) = 0 ….(1)
Also, the plane passes through points (3, 4, 2)
a(3 – 2) + b(4 – 2)+ c(2 + 1) = 0
or, a + 2b + 3c = 0 …(2)
As we know that the line ![]() is parallel to plan a2x + b2y + c2z + d2 = 0, when a1a2 + b1b2 + c1c2 = 0
is parallel to plan a2x + b2y + c2z + d2 = 0, when a1a2 + b1b2 + c1c2 = 0
According to the question, the plane(1) is parallel to the line whose direction ratios are 7, 0, 6
So, 7a + 0b + 6c = 0 …(3)
Now, on solving the equation (1), (2), and (3), we have,
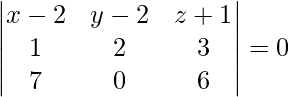
⇒ 12x + 15y – 14z – 68 = 0 is the required equation.
问题 13. 求直线之间的角度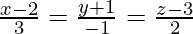 平面 3x + 4y + z + 5 = 0。
平面 3x + 4y + z + 5 = 0。
解决方案:
Given that the equation of line is ![]() and the equation of the plane is 3x + 4y + z + 5 = 0
and the equation of the plane is 3x + 4y + z + 5 = 0
So, ![]()
![]()
Angle between a line and a plane is
![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
Thus, ![]()