问题1.找到通过点(1、1、1),(1,-1、1)和(-7,-3,-5)的平面的矢量方程
解决方案:
Given that, plane is passing through
(1, 1, 1), (1, -1, 1) and (-7, -3, -5)
We know that, equation of plane passing through 3 points,
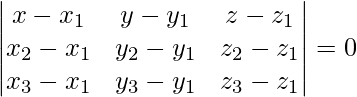
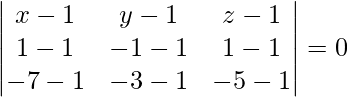

(x – 1)(12 – 0) – (y – 1)(0 – 0) + (z – 1)(0 – 16) = 0
(x – 1)(12) – (y – 1)(0) + (z – 1)(-16) = 0
12x – 12 – 0 – 16z + 16 = 0
12x – 16z + 4 = 0
Dividing by 4,
3x – 4z + 1 = 0
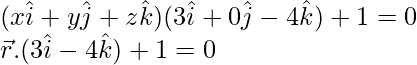
Equation of the required plane,
![]()
问题2。找到通过点P(2,5,-3),Q(-2,-3,5)和R(5,3,-3)的平面的矢量方程。
解决方案:
Let P(2, 5, -3), Q(-2, -3, 5) and R(5, 3, -3) be the three points on a plane having position vectors ![]() respectively. Then the vectors
respectively. Then the vectors ![]() and
and ![]() are in the same plane. Therefore,
are in the same plane. Therefore, ![]() is a vector perpendicular to the plane.
is a vector perpendicular to the plane.
Let = ![]()
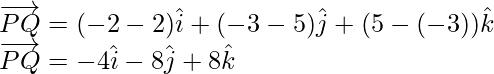
Similarly,
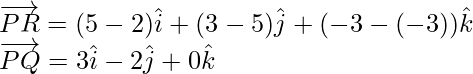
Thus

The plane passes through the point P with position vector ![]()
Thus, its vector equation is
![]()
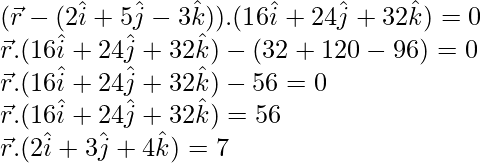
问题3.找到通过点A(a,0,0),B(0,b,0)和C(0,0,c)的平面的矢量方程。将其缩小为正常形式。如果飞机ABC距原点的距离为p,则证明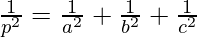
解决方案:
Let A(a, 0, 0), B(0, b, 0) and C(0, 0, c) be three points on a plane having their position vectors ![]() respectively. Then vectors
respectively. Then vectors ![]() and
and ![]() are in the same plane. Therefore,
are in the same plane. Therefore, ![]() is a vector perpendicular to the plane.
is a vector perpendicular to the plane.
Let ![]()
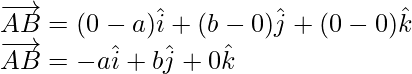
Similarly,
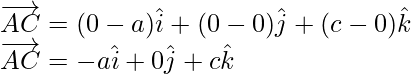
Thus
![]()
![]()
= | -a b 0 |
-a 0 c
![]()
![]()
The plane passes through the point P with position vector ![]()
Thus, the vector equation in the normal form is

The vector equation of a plane normal to the unit vector ![]() and at a distance ‘d’ from the origin is
and at a distance ‘d’ from the origin is ![]() ….(2).
….(2).
Given that the plane is at a distance ‘p’ from the origin.
Comparing equations (1) and (2), we have,
d = p = 
问题4.找到通过点(1、1,-1),(6、4,-5)和(-4,-2、3)的平面的矢量方程。
解决方案:
Let P(1, 1, -1), Q(6, 4, -5) and R(-4, -2, 3) be three points on a plane having position vectors ![]() respectively. Then the vectors
respectively. Then the vectors ![]() are in the same plane. Therefore,
are in the same plane. Therefore, ![]() is a vector perpendicular to the plane.
is a vector perpendicular to the plane.
Let ![]()

Similarly,

Thus
Here, ![]()
Therefore, the given points are collinear.
Thus, ![]() where, 5a + 3b – 4c = 0
where, 5a + 3b – 4c = 0
The plane passes through the point P with position vector ![]()
Thus, its vector equation is
![]() , where, 5a + 3b – 4c = 0
, where, 5a + 3b – 4c = 0
问题5.找到通过点的平面的矢量方程
![]()
解决方案:
Let A, B, C be the points with position vector ![]()
respectively. Then
![]() = Position vector of B – Position vector of A
= Position vector of B – Position vector of A
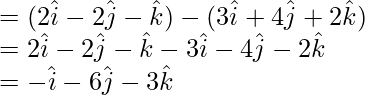
![]() = Position vector of C – Position vector of B
= Position vector of C – Position vector of B
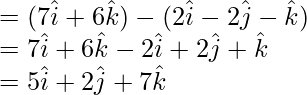
A vector normal to A, B, C is a vector perpendicular to ![]()
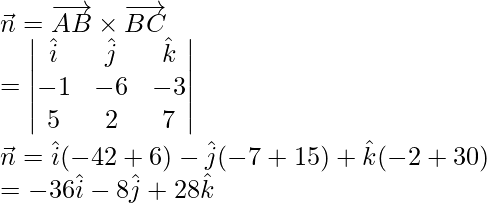
As we know that, equation of a plane passing through vector ![]() and perpendicular to vector
and perpendicular to vector ![]() is given by,
is given by,
![]()
Put ![]() and
and ![]() in equation (1)
in equation (1)
![]()
= (3)(-36) + (4)(-8) + (2)(28)
= -108 – 32 + 56
= -140 + 56
![]() = -84
= -84
Dividing by (-4), we will get
![]()
Equation of required plane is,
![]()