第 12 课 RD Sharma 解决方案 - 第 29 章飞机 - 练习 29.7
问题 1. 求下列平面的标量积形式的向量方程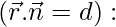
解决方案:
(i) ![]()
Here, ![]()
We know that, ![]() represent a plane passing through a point having position vector
represent a plane passing through a point having position vector ![]() and parallel to vectors
and parallel to vectors ![]() and .
and .![]()
Here, ![]()
The given plane is perpendicular to a vector
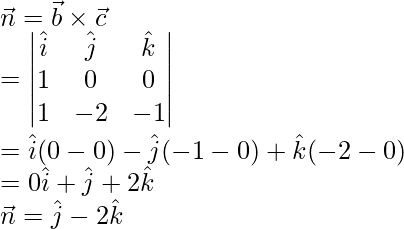
We know that vector equation of plane in scalar product form is,
![]() —(Equation-1)
—(Equation-1)
Put and
![]() in (Equation-1),
in (Equation-1),
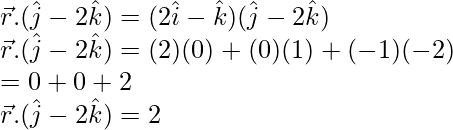
The equation is required form is,
![]()
(ii) ![]()
Here,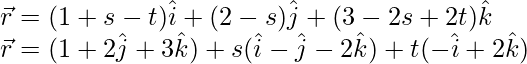
We know that, ![]() represent a plane passing through a point having position vector
represent a plane passing through a point having position vector ![]() and parallel to vectors
and parallel to vectors ![]() and
and ![]()
Here, ![]()
The given plane is perpendicular to a vector
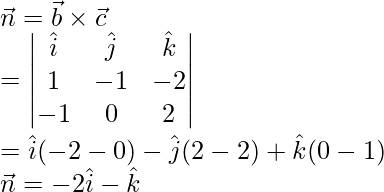
We know that, vector equation of a plane is scalar product is,
![]() —(Equation-1)
—(Equation-1)
Put value of ![]() and
and in (Equation-1)
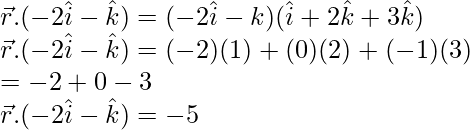
Multiplying both the sides by (-1),
![]()
The equation in the required form,
![]()
(iii) ![]()
Given, equation of plane,
![]()
We know that, ![]() is the equation of a plane passing through point
is the equation of a plane passing through point ![]() and parallel to
and parallel to ![]() and
and ![]() .
.
Here, ![]()
The given plane is perpendicular to a vector
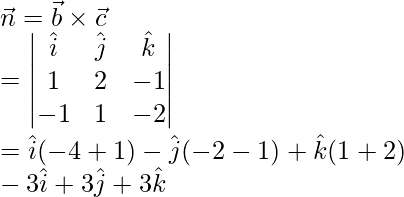
We know that, equation of plane in scalar product form is given by,
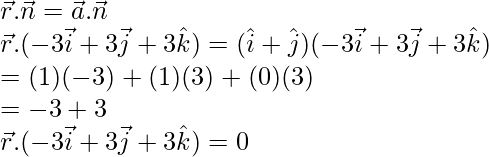
Dividing by 3, we get
![]()
Equation in required form is,
![]()
(iv) ![]()
![]()
Plane is passing through ![]() and parallel to b
and parallel to b ![]() and
and ![]()
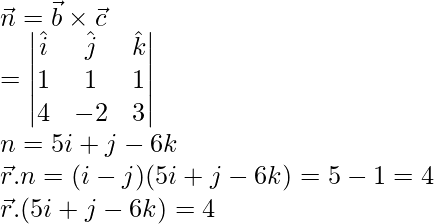
问题 2. 求下列平面方程的笛卡尔形式:
解决方案:
(i) ![]()
Here, given equation of plane is,
![]()
We know that, ![]() represents the equation of a plane passing through a vector
represents the equation of a plane passing through a vector ![]() and parallel to vector
and parallel to vector ![]() and
and ![]() .
.
Here, ![]()
Given plane is perpendicular to vector
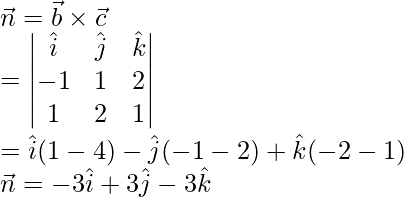
We know that, equation of plane in the scalar product form,
![]() —Equation-1
—Equation-1
Put the value of ![]() and
and in Equation-1,
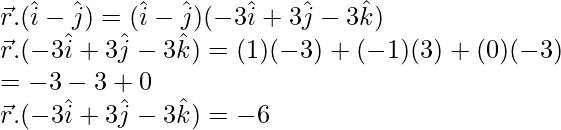
Put 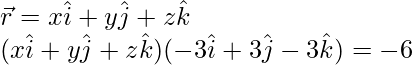
(x)(-3) + (y)(3) + (z)(-3) = -6
-3x + 3y – 3z = -6
Dividing by (-3), we get
x – y + z = 2
Equation in required form is,
x – y + z = 2
(ii) ![]()
Given, equation of plane,
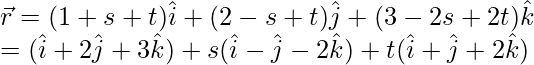
We know that, ![]() represents the equation of a plane passing through the vector
represents the equation of a plane passing through the vector ![]() and parallel to vector
and parallel to vector ![]() and
and ![]()
Here, 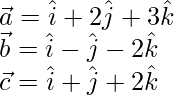
The given plane is perpendicular to vector
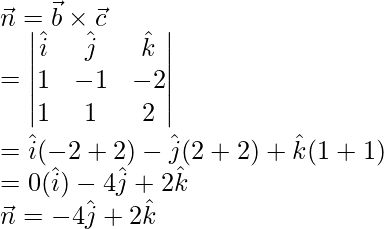
We know that, equation of plane in scalar product form is given by,
![]() —Equation-1
—Equation-1
Put, the value of ![]() and
and in equation-1
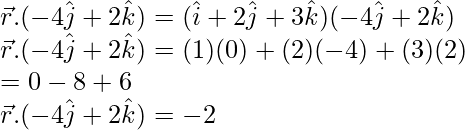
Put ![]()
![]()
(x)(0) + (y)(-4) + (z)(2) = -2
-4y + 2z = -2
The equation in required form is,
2y – z = 1
问题 3. 求下列平面的非参数形式的向量方程:
解决方案:
(i) ![]()
Given, equation of plane is,
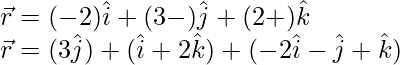
We know that, ![]() represents the equation of a plane passing through a point
represents the equation of a plane passing through a point ![]() and parallel to vector
and parallel to vector ![]() and
and ![]() .
.
Given,
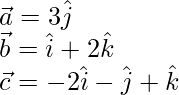
The given plane is perpendicular to
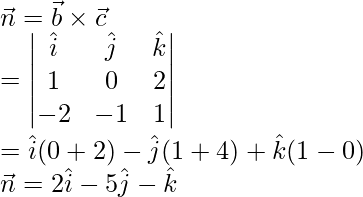
Vector equation of plane in non-parametric form is.
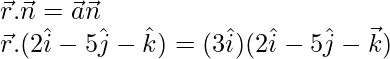
= (0)(2) + (3)(-5) + (0)(-1)
= 0 – 15 + 0
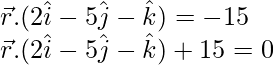
The required form of equation is,
![]()
(ii) ![]()
Given, equation of plane is,
![]()
We know that, ![]() represents the equation of a plane passing through a vector
represents the equation of a plane passing through a vector ![]() and parallel to vector
and parallel to vector ![]() and
and ![]() .
.
Here,
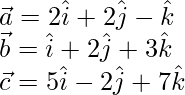
The given plane is perpendicular to vector
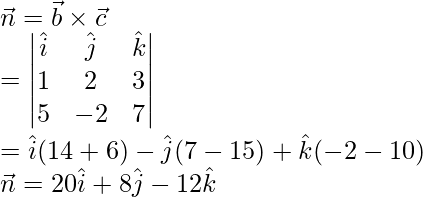
We know that, equation of a plane in non-parametric form is given by,
![]()
![]()
= (2)(20) + (2)(8) – (-1)(-12)
=40 + 16 + 12
![]()
Dividing by 4,
![]()
Equation of plane in required form is,
![]()