第 12 类 RD Sharma 解决方案 - 第 29 章飞机 - 练习 29.11 |设置 2
问题 14. 求通过平面 x – 2y + z = 1 和 2x + y + z = 8 的交点并平行于方向比与 1、2、1 成比例的直线的平面方程。另外,求(1, 1, 1) 与该平面的垂直距离。
解决方案:
As we know that the equation of the plane passing through the line of intersection of two planes are
(a1x + b1y + c1z + d1) + λ(a2x + b2y + c2z + d2) = 0
So, the equation of the plane passes through the intersection of the planes x – 2y + z = 1 and 2x + y + z = 8 is
(1 + 2λ)x + (-2 + λ)y + (1 + λ)z – 1 – 8λ = 0 ….(1)
Also, given that this plane is parallel to the line whose direction ratios are proportional to 1, 2, 1.
⇒ (1 + 2λ)1 + (-2 + λ)2 + (1 + λ)1 = 0
⇒ 1 + 2λ – 4 + 2λ + 1 + λ = 0
⇒ 5λ – 2 = 0
⇒ λ = 2/5
Now put the value of λ in (1), we have:
9x – 8y + 7z – 21 = 0 is the required equation.
And the perpendicular distance of plane from (1, 1, 1) is
= 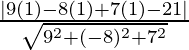
= ![]() units.
units.
问题 15. 显示何时行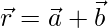 平行于平面
平行于平面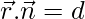 .显示该行
.显示该行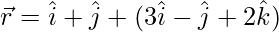 平行于平面
平行于平面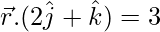 .另外,求直线与平面之间的距离。
.另外,求直线与平面之间的距离。
解决方案:
The plane passes through the point with position vector ![]() and is parallel to the vector
and is parallel to the vector ![]()
Given equation of the plane is ![]() or
or ![]()
So, the normal vector is ![]() and d = 3.
and d = 3.
Now, ![]()
= 0 – 2 + 2 = 0
So, ![]() is perpendicular to
is perpendicular to ![]()
Hence, the given line is parallel to the given plane.
As we know that the distance between the line and parallel plane is the distance between any point on the line and the given plane.
So, Distance(d) = ![]()
= ![]()
= ![]() units.
units.
问题 16. 证明这条线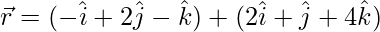 平行于平面
平行于平面 .另外,求两者之间的距离。
.另外,求两者之间的距离。
解决方案:
The plane passes through the point with the position vector ![]() and is parallel to the vector
and is parallel to the vector ![]() [Tex]\vec{b}[/Tex]
[Tex]\vec{b}[/Tex]
Given plane is ![]() or
or ![]()
So, the normal vector is ![]() and d = 3.
and d = 3.
Now, ![]()
= 0 – 2 + 2 = 0
So, it is perpendicular to ![]() .
.
Hence, the given line is parallel to the plane.
As we know that the distance between a line and a parallel plane is the distance between any point on the line and the given plane.
so, Distance(d) = ![]()
= ![]()
= 1/√6 units.
问题 17. 通过平面 3x – 4y + 5z = 10 和 2x + 2y – 3z = 4 并平行于线 x = 2x = 3z 求平面方程。
解决方案:
As we know that the equation of the plane passing through the line of intersection of two planes are
(a1x + b1y + c1z + d1) + λ(a2x + b2y + c2z + d2) = 0
So, the equation of the plane passes through the intersection of the
planes 3x – 4y + 5z = 10 and 2x + 2y – 3z = 4 is
(3 + 2λ)x + (-4 + 2λ)y + (5 – 3λ)z – 10 – 4λ = 0 ….(1)
Given that the equation of line is x = 2x = 3z.
Now, dividing this equation by 6, we get,
![]()
So we get the direction ratios of this line are proportional to 6, 3, 2.
Now, the normal to the plane is perpendicular to the line whose direction ratios are 6, 3, 2.
⇒ (3 + 2λ)6 + (-4 + 2λ)3 + (5 – 3λ)2 – 10 – 4λ = 0
⇒ λ = -4/3
Now put the value of λ in eq(1), we get,
x – 20y + 27z = 14 is the required equation.
问题 18. 求通过点 (1, 2, -4) 并平行于直线的平面方程的向量和笛卡尔形式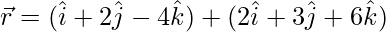 和
和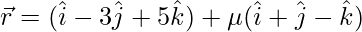 .另外,求该点到所获得的平面的距离。
.另外,求该点到所获得的平面的距离。
解决方案:
Given that the equations of the lines are ![]()
![]()
As we know that the vector equation of a plane passing through a point ![]() and parallel to
and parallel to ![]() and
and ![]() is
is
![]()
So, ![]()
![]()
Now, the vector equation of the plane is ![]()
![]()
![]()
The cartesian equation of the plane is
-9x + 8y – z = 11
Now the distance of the point(9, -8, -10) from the plane is
![]()
D = √146
问题 19. 求通过点 (3, 4, 1) 和 (0, 1, 0) 并平行于直线的平面方程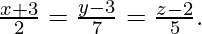
解决方案:
When the plane passes through points (3, 4, 1), then the equation of the plane is
a(x – 3) + b(y – 4) + c(z – 1)=0 ….(1)
When this plane passes through points (0, 1, 0), then the equation of the plane is
a(0 – 3) + b(1 – 4) + c(0 – 1) = 0
⇒ 3a + 3b + 3c = 0 …..(2)
Also, given that the plane(i.e., eq(1)) is parallel to line.
So the normal of the plane(i.e., eq(1)) is perpendicular to the line so,
2a + 7b + 5c = 0 …..(3)
Now, on solving eq(1), (2), and (3), we get
8x – 13y + 15z + 13 = 0 is the required equation.
问题20.求直线所在点的坐标 并与平面 x – y + z – 5 = 0 相交。同时求直线与平面之间的夹角。
并与平面 x – y + z – 5 = 0 相交。同时求直线与平面之间的夹角。
解决方案:
Given that the equation of line is ![]()
⇒ x = 3λ + 2, y = 4λ – 1, z = 2λ + 2 ….(1)
As we know that (x, y, z) intersect the plane x – y + z – 5 = 0,
So,
3λ + 2 – (4λ – 1) + 2λ + 2 – 5 = 0
⇒ λ = 0
Now, put this value in eq(1), we get
x = 2, y = -1, z = 2
The angle between the line and the plane is
![]()
Here, ![]()
![]()
⇒ ![]()
⇒![]()
⇒ ![]()
问题 21. 求通过 (1, 2, 3) 且垂直于该平面的平面的向量方程 .
.
解决方案:
Let us assume that the direction ratios are a, b, c
Given that the line passes through (1, 2, 3), so the equation of the line is
![]() ….(1)
….(1)
And the line is perpendicular to the plane ![]()
So, the line is parallel to the normal of the plane.
Now, the direction ratios are proportional to those of the given plane.
⇒ a = λ, b = 2λ, c = -5λ
Put these values in eq(1), we get
![]()
So, the vector form is
![]() is the required equation.
is the required equation.
问题 22. 求直线之间的角度 平面 10x + 2y – 11z = 3。
平面 10x + 2y – 11z = 3。
解决方案:
Given that the equation of the line is ![]() and the equation of the plane is 10x + 2y – 11z = 3
and the equation of the plane is 10x + 2y – 11z = 3
So, ![]()
![]()
As we know that the angle between a line and a plane is
![]()
= ![]()
⇒ θ = sin−1(−8/21)
问题 23. 求通过 (1, 2, 3) 且平行于平面的直线的向量方程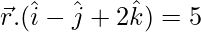 和
和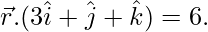
解决方案:
Let us assume, ab, b, c are the direction ratios of the required line.
Given that the line is passes through (1, 2, 3). So the equation of the line is
![]() …(1)
…(1)
Also given that eq(1) is parallel to the planes ![]() and
and ![]() .
.
So, a – b + 2c = 0 …(2)
3a + b + z = 0 …(3)
Now on solving eq(2) and (3), we get
![]()
![]()
=> a = -3λ, b = 5λ, c = 4λ
Now put these values in eq(1), we get
![]() which is the cartesian form of the required line.
which is the cartesian form of the required line.
问题 24. 求 λ 的值使得直线 垂直于平面 3x - y - 2z = 7。
垂直于平面 3x - y - 2z = 7。
解决方案:
Given that the equation of line is ![]() and
and
the equation of the plane is 3x − y − 2z = 7 and the line is perpendicular to the plane
So, the direction ratios of the given line are proportional to 6, λ ,-4.
and the direction ratios of the plane are 3, -1, -2.
Thus the line is parallel to the given plane, the line is perpendicular
to the normal of the given plane. So,
⇒ (6)(3) + (-1)(-4) + (-2 )(11) = 0
⇒ λ = 26
问题 25. 求通过点 (-1, 2, 0), (2, 2, -1) 并平行于直线的平面方程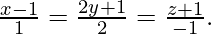
解决方案:
The general equation of the plane passing through the point (−1, 2, 0) is
a(x+1) + b(y-2) + c( z – 0) = 0 ….(1)
This plane passes through the point (2, 2,−1), we get
a(2 + 1) + b(2 – 2) + c( -1 – 0) = 0
⇒ 3a – c = 0 ….(2)
Now, a, b, c are the direction ratio of the normal to the plane (1) and
the normal is perpendicular to the line, so
a + 2b + c = 0 ….(3)
Now on solving eq(2) and (3), we get
![]()
a = λ, b = -2 λ, c = 3λ
Now put all these values in eq(1), we get
λ(x + 1) – 2λ(y – 2) + 3λ(z – 0) = 0
x + 2y + 3z = 3
Thus, the equation of the required plane is x + 2y + 3z = 3.