第 12 类 RD Sharma 解决方案 - 第 29 章飞机 - 练习 29.15 |设置 1

问题 1. 求平面 3x + 4y – 6z + 1 = 0 中点 (0, 0, 0) 的图像。

解决方案：

According to the question we have

Plane = 3x + 4y – 6z + 1 = 0

Line passing through origin and perpendicular to plane is given by

$\frac{x}{3}=\frac{y}{4}=\frac{z}{-6}=r$

So, let the image of (0, 0, 0) = (3r, 4r, -6r) 

The midpoint of (0, 0, 0) and (3r, 4r, -6r) lies on the given plane

3(3r/2) + 2(4r) – 3(-6y) + 1 = 0

30.5y = -1

r = -2/61

So, the image is (-6/61, -8/61, 12/61) 

问题 2. 求点 (1, 2, -1) 在平面 3x – 5y + 4z = 5 的反射

解决方案：

According to the question we have to find the reflection of 

the point P(1, 2, -1) in the plane 3x – 5y + 4z = 5

So, let Q = reflection of the point P 

R = midpoint of PQ.

Then, R lies on the plane 3x – 5y + 4z = 5.

Now, the direction ratios of PQ are proportional to 3, -5, 4 and 

PQ is passing through (1, 2, -1).

So, equation of PQ is,

$\frac{x-1}{3}=\frac{y-2}{-5}=\frac{z+1}{4}=λ$

Let Q be (3λ + 1, -5λ + 2, 4λ – 1)

The coordinates of R are = $\left(\frac{3λ+1+1}{2},\frac{-5λ+2+2}{2},\frac{4λ-1-1}{2}\right)=\left(\frac{3λ+2}{2},\frac{-5λ+4}{2},\frac{4λ-2}{2}\right)$

Since, R lies on the given plane i.e., 3x – 5y + 4z = 5

Therefore, $3\left(\frac{3λ+2}{2}\right)-5\left(-\frac{5λ+4}{2}\right)+4\left(\frac{4λ-2}{2}\right)=5$

9λ + 6 + 25λ – 20 + 16λ – 8 = 10

50λ – 22 = 10

50λ = 32

λ = 16/25

Q = (3λ + 1, -5λ + 2, 4λ -1)         -Equation(1)

Now, put the value of λ in equation (1), we get,

= (3(16/25)+1, -5(16/25)+2, 4(16/25)-1)

= ((48/25)+1,  (-16/5)+2, (64/25)-1)

= (73/25, -6/5, 39/25)

Hence, the reflection of point (1, 2, -1) = (73/25, -6/5, 39/25)

问题 3. 求点 (5, 4, 2) 到直线画的垂线的脚坐标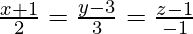$\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}$ .因此或以其他方式推导出垂线的长度。

解决方案：

According to the question we have to find foot of the perpendicular, say Q,

drawn from point P(5, 4, 2) to the line $\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}=λ$

So, Let us assume Q = (2λ – 1, 3λ + 3, -λ + 1)          -Equation(1)

Direction ratio of line PQ are = (2λ – 6, 3λ – 1, -λ – 1)

Here, the line PQ is perpendicular to line the given line AB

So, 

a₁a₂ + b₁b₂ + c₁c₂ = 0

(2λ – 6)(2) + (3λ – 1)(3) + (-λ – 1)(-1) = 0

4λ – 12 + 9λ – 3 + λ + 1 = 0

14λ – 14 = 0

λ = 14/14

λ = 1

So, put the value of λ in equation(1), we get

= (2(1) – 1, 3(1) + 3, -(1) + 1)

= (2 – 1, 3 + 3, -1 +1)

= (1, 6, 0)

Now, we find the length of perpendicular PQ using distance formula 

$= \sqrt{(5-1)^2+(4-6)^2+(2-0)^2}\\ = \sqrt{16+4+4}\\$

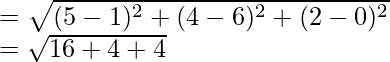
= √24

= 2√6

So, the foot of the perpendicular is (1, 6, 0)

Length of the perpendicular is 2√6 units.

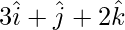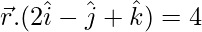问题4.用位置向量求点的图像$3\hat{i}+\hat{j}+2\hat{k}$在飞机上$\vec{r}.(2\hat{i}-\hat{j}+\hat{k})=4$ .还求垂线脚的位置向量和垂线方程通过$3\hat{i}+\hat{j}+2\hat{k}$ .

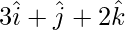解决方案：

According to the question we have to find image of the point P(3, 1, 2) 

in the plane $\vec{r}.(2\hat{i}-\hat{j}+\hat{k})=4$ or 2x – y + z = 4.

Let Q be the image of the point P.

So,

The direction ratios of normal to the point = 2, -1, 1

The direction ratios of line PQ perpendicular to 2, -1, 1 and

PQ is passing through (3, 1, 2)

So equation of PQ is

$\frac{x-3}{2}=\frac{y-1}{-1}=\frac{z-2}{1}=λ$      

General point on the line PQ is = (2λ + 3, -λ + 1, λ + 2)

Let us assume Q = (2λ + 3, -λ + 1, λ + 2)           -Equation(1)

Let R be the mid point of PQ. Then,

Coordinates of R =  $\left(\frac{2λ+3+3}{2},\frac{-λ+1+1}{2},\frac{λ+2+2}{2}\right)=\left(\frac{2λ+6}{2},\frac{-λ+2}{2},\frac{λ+4}{2}\right)$

Since, R lies on the plane 2x – y + z = 4, we get

$2\left(\frac{2λ+6}{2}\right)-\left(\frac{-λ+2}{2}\right)+\left(\frac{λ+4}{2}\right)=4$

4λ + 12 + λ – 2 + λ + 4 = 8

6λ = 8 – 14

λ = -6/6

λ = -1 

So, put the value of λ in equation(1), we get

Image of P = Q(2 (-1) + 3, – (-1) + 1, -1 + 2)

Image of P = (1, 2, 1)

Equation of the perpendicular line through $3\hat{i}+\hat{j}+2\hat{k}$ is

$\vec{r}=3\hat{i}+\hat{j}+2\hat{k}+λ(2\hat{i}-\hat{j}+\hat{k})$

Position vector of the image point is

$3\hat{i}+\hat{j}+2\hat{k}+λ(2\hat{i}-\hat{j}+\hat{k})=(3+2λ)\hat{i}+(1-λ)\hat{j}+(2+k)\hat{k}$

Position vector of the foot of the perpendicular is

$\frac{[(3+2λ)\hat{i}+(1-λ)\hat{j}+(2+k)\hat{k}]+[3\hat{i}+\hat{j}+2\hat{k}]}{2}$

$=(3+λ)\hat{i}+(1-\frac{λ}{2})\hat{j}+(2+\frac{λ}{2})\hat{k}$

By putting the value of λ in the position vector of the foot of the perpendicular is 

$2\hat{i}+\frac{3}{2}\hat{j}+\frac{3}{2}\hat{k}$

问题 5. 求从点 (1, 1, 2) 到平面 2x – 2y + 4z + 5 = 0 的垂线脚的坐标。另外，求垂线的长度。

解决方案：

According to the question we have,

Plane = 2x – 2y + 4z + 5 = 0         -Equation(1)

Point = (1, 1, 2)

and find the coordinates of the foot of the perpendicular

$= \left|\frac{2-2+8+5}{\sqrt{1+1+4}}\right|=\frac{13}{\sqrt{6}}$ 

Let us assume that the foot of perpendicular = (x, y, z). 

So, DR’s are in proportional

$\frac{x-1}{2}=\frac{y-1}{-2}=\frac{z-2}{4}=k$

x = 2k + 1

y = -2k + 1

z = 4k + 2

Substitute (x, y, z) = (2k + 1, -2k + 1, 4k + 2) in the equation(1), we get

2x – 2y + 4z + 5 = 0

4k + 2 + 4k – 2 + 16k + 8 + 5 = 0

24k = -13

k = -13/24

So, the coordinates of the foot of the perpendicular (x, y, z) = (-1/12, 5/3, -1/6)

问题 6. 求点 (1, -2, 3) 到平面 x – y + z + 5 沿平行于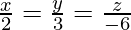$\frac{x}{2}=\frac{y}{3}=\frac{z}{-6}$

解决方案：

According to the question, we have to find the distance of point P(1, -2, 3) 

from the plane x – y + z = 5 measured 

parallel to line AB, $\frac{x}{2}=\frac{y}{3}=\frac{z}{-6}$

Let us assume Q = Mid point of the line joining P to plane.

We have, PQ parallel to line AB

The direction ratios of line PQ are proportional to direction ratios of line AB

The direction ratios of line PQ = 2, 3, -6 

PQ is passing through point P(1, -2, 3).

Thus, the equation of PQ is,

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\\ \frac{x-1}{2}=\frac{y+2}{3}=\frac{z-3}{-6}=λ\\$

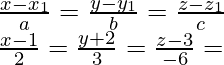
The general point on the line PQ = (2λ + 1, 3λ – 2, -6λ + 3)

Suppose the coordinates of Q = (2λ + 1, 3λ – 2, -6λ + 3)

Thus, Q lies on the plane x – y + z = 5

(2λ + 1) – (3λ – 2) + (-6λ + 3) = 5

2λ + 1 – 3λ + 2 – 6λ + 3 = 5

-7λ = -1

λ = 1/7

Coordinate of Q = (2λ + 1, 3λ – 2,  -6λ + 3)          -Equation(1)

Now, put the value of λ in equation(1), we get

Q = (2(1/7)+1, 3(1/7)-2, -6(1/7)+3)

Q = (9/7, -11/7, 15/7)

Now, we find the distance between (1, -2, 3) and plane = PQ

$=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}\\ =\sqrt{(1-\frac{9}{7})^2+(-2+\frac{11}{7})^2+(3-\frac{15}{7})^2}\\ =\sqrt{\frac{4}{49}+\frac{9}{49}+\frac{36}{49}}\\ =\sqrt{\frac{49}{49}}$

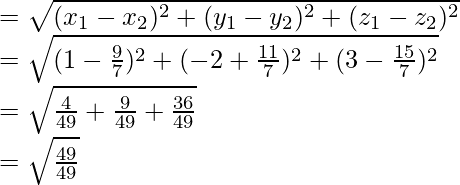
= 1

Hence, the required distance is 1 unit.

问题 7. 求从点 (2, 3, 7) 到平面 3x – y – z = 7 的垂线的脚坐标。另外，求垂线的长度。

解决方案：

Let us assume that Q be the foot of the perpendicular.

Now, the direction ratios of normal plane is 3, -1, -1

Line PQ is parallel to normal to plane

Direction ratios of PQ are proportional to 3, -1, -1 

PQ is passing through point P(2, 3, 7)

So, 

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\\ \frac{x-2}{3}=\frac{y-3}{-1}=\frac{z-7}{-1}=λ$

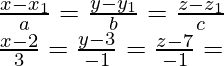
The general point on the line PQ

= (3λ + 2, -λ + 3, -λ + 7)

Coordinates of Q = (3λ + 2, -λ + 3, -λ + 7)         -Equation(1)

Point Q lies on the plane 3x – y – z = 7

Thus,

3(3λ + 2) – (-λ + 3) – (-λ + 7) = 7

9λ + 6 + λ – 3 + λ – 7 = 7

11λ = 7 + 4

11λ = 11

λ = 11/11

λ = 1

Now, put the value of λ in equation(1), we get

Q = (3(1) + 2, -(1) + 3, -(1) + 7)

Q = (5, 2, 6)

Find the length of the perpendicular PQ

$=\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2}\\ =\sqrt{(2-5)^2+(3-2)^2+(7-6)^2}\\ =\sqrt{9+1+1}\\$

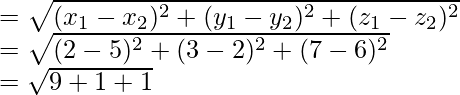
= √11