第12类RD Sharma解决方案–第29章飞机–练习29.14

问题1.找到线之间的最短距离$\frac{x-2}{-1}=\frac{y-5}{2}=\frac{z-0}{3}$和$\frac{x-0}{2}=\frac{y+1}{-1}=\frac{z-1}{2}$ 。

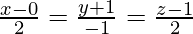解决方案：

Let us consider

$P_1=\frac{x-2}{-1}=\frac{y-5}{2}=\frac{z-0}{3}\\ P_2=\frac{x-0}{2}=\frac{y+1}{-1}=\frac{z-1}{2}$

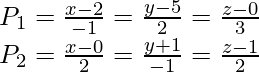
According to the equations line P₁ passes through the point P(2, 5, 0)

And the equation of a plane containing line P₂ is

a(x – 0) + b(y + 1) + c(z – 1) = 0          -(1)

Where 2a – b + 2c = 0

If it is parallel to line P₁ then

-a + 2b + 3c = 0

So, 

$\frac{a}{-7}=\frac{b}{-8}=\frac{c}{3}$

Now, substitute the value of a, b, c in the eq(1) we get

a(x – 0) + b(y + 1) + c(z – 1) = 0

-7(x – 0) – 8(y + 1) + 3(z – 1) = 0

-7x – 8y – 8 + 3z – 3 = 0

7x + 8y – 3z + 11 = 0          -(2)

So, this is the equation of the plane that contain line P₂ and parallel to line P₁.

Hence, the shortest distance between P₁ and P₂ = Distance between point P(2, 5, 0) and plane (2)

$=\left|\frac{14+40+11}{\sqrt{7^2+8^2+(-3)^2}}\right|=\frac{65}{\sqrt{122}}$

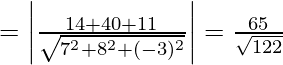
问题2.找到线之间的最短距离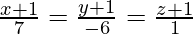$\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$和$\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$ 。

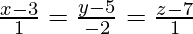解决方案：

Let us consider

$P_1:\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$

$P_2:\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$

Let us assume the equation of the plane containing P₁ is a(x + 1) + b(y + 1) + c(z+1) = 0

Plane is parallel to P₁ = 7a – 6b + c = 0          -(1)

Plane is parallel to P₂ = a – 2b + c = 0          -(2)

On solving eq(1) and eq(2), we get,

$\frac{a}{-6+2}=\frac{b}{1-7}=\frac{c}{-14+6}\\ \frac{a}{-4}=\frac{b}{-6}=\frac{c}{-8}$

The equation of the plane is -4(x + 1) – 6(y + 1) – 8(z + 1) = 0

Final equation of plane is 4(x + 1) + 6(y + 1) + 8(z + 1) = 0 

问题3.找到线之间的最短距离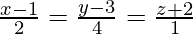$\frac{x-1}{2}=\frac{y-3}{4}=\frac{z+2}{1}$和3x – y – 2z + 4 = 0，2x + y + z + 1 = 0。

解决方案：

The equation of a plane containing the line 3x – y – 2z + 4 = 0, 2x + y + z + 1 = 0 is 

x(2λ + 3) + y(λ – 1) + z(λ – 2) + λ + 4 = 0          -(1)

If it is parallel to the line $\frac{x-1}{2}=\frac{y-3}{4}=\frac{z+2}{1}$ then,

2(2λ + 3) + 4(λ – 1) + (λ – 2) = 0

λ = 0

On putting λ = 0 in eq(1) we get,

3x – y – 2z + 4 = 0          -(2)

As this equation of the plane consist the second line and parallel to the first line.

It is clear that the line $\frac{x-1}{2}=\frac{y-3}{4}=\frac{z+2}{1}$ passes through the point (1, 3, -2)

So, the shortest distance ‘D’ between the given lines is equal to the 

length of perpendicular from point (1, 3, -2) on the plane (2)

D = $\left|\frac{3-3+4+4}{\sqrt{1+9+4}}\right|=\frac{8}{\sqrt{14}}$