第12类RD Sharma解决方案–第29章飞机–练习29.3 |套装1

问题1.找到通过具有位置矢量的点的平面的矢量方程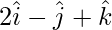$2\hat{i}-\hat{j}+\hat{k}$并垂直于向量$4\hat{i}+2\hat{j}-3\hat{k}$ 。

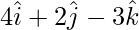解决方案：

As we know that the vector equation of a plane passing through a point $\vec{a}$and normal to $\vec{n}$is

$(\vec{r}-\vec{a}).\vec{n} =0$

⇒$\vec{r}.\vec{n}=\vec{a}.\vec{n}$

Here, $\vec{a}=2\hat{i}-\hat{j}+\hat{k}$ and $\vec{n}=4\hat{i}+2\hat{j}-3\hat{k}$

So, the equation of the required equation is 

$\vec{r}.(4\hat{i}+2\hat{j}-3\hat{k})=(2\hat{i}-\hat{j}+\hat{k})(4\hat{i}+2\hat{j}-3\hat{k})$

⇒ $\vec{r}.(4\hat{i}+2\hat{j}-3\hat{k})$ = (4)(2) + (2)(-1) + (-3)(1)

⇒ $\vec{r}.(4\hat{i}+2\hat{j}-3\hat{k})$ = 8 – 2 – 3

⇒ $\vec{r}.(4\hat{i}+2\hat{j}-3\hat{k})=3$

Hence, the required equation is 

$\vec{r}.(4\hat{i}+2\hat{j}-3\hat{k})-3=0$

问题2.求向量方程为的平面方程的笛卡尔形式

(一世) 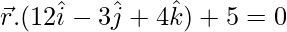$\vec{r}.(12\hat{i}-3\hat{j}+4\hat{k})+5=0$    

解决方案：

Given vector equation of a plane,

$\vec{r}.(12\hat{i}-3\hat{j}+4\hat{k})+5=0$

Since $\hat{i}, \hat{j}, \hat{k}$denotes the position vector of an arbitrary point (x, y, z) on the plane. 

Therefore, putting $\vec{r}=x\hat{i}+y\hat{j}+j\hat{k}$

⇒ $(x\hat{i}+y\hat{j}+j\hat{k}).(12\hat{i}-3\hat{j}+4\hat{k})+5=0$

⇒ (x)(12) + (y)(-3) + (z)(4) = -5

⇒ 12x – 3y + 4z + 5 = 0

So, this is the required cartesian equation of the plane.

(ii) 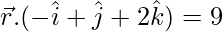$\vec{r}.(-\hat{i}+\hat{j}+2\hat{k})=9$

解决方案：

Given vector equation of a plane,

$\vec{r}.(-\hat{i}+\hat{j}+2\hat{k})=9$

Since $\hat{i}, \hat{j}, \hat{k}$ denotes the position vector of an arbitrary point (x, y, z) on the plane. 

Therefore, putting $\vec{r}=x\hat{i}+y\hat{j}+j\hat{k}$    

⇒$(x\hat{i}+y\hat{j}+j\hat{k}).(-\hat{i}+\hat{j}+2\hat{k})=9$

⇒ (x)(-1) + (y)(1) + (z)(2) = 9

⇒ -x + y + 2z = 9

So, this is the required cartesian equation of the plane.

问题3.找到坐标平面的矢量方程。

解决方案：

Vector equation of XY-Plane:

The XY- Plane passes through origin whose position vector is $\vec{a}=\vec{0}$and 

perpendicular to Z-axis whose position vector is $\vec{k}$

So the equation of the XY plane is $\vec{r}.\vec{n}=\vec{a}.\vec{n}$

⇒ $\vec{r}.\vec{k}=\vec{0}.\vec{k}$

$\vec{r}.\vec{k}=0$

Vector equation of XZ-Plane:

The XZ- Plane passes through origin whose position vector is $\vec{a}=\vec{0}$

and perpendicular to Y-axis whose position vector is $\vec{j}$

So the equation of the XZ plane is $\vec{r}.\vec{n}=\vec{a}.\vec{n}$

⇒ $\vec{r}.\vec{j}=\vec{0}.\vec{j}$

$\vec{r}.\vec{j} =0$

Vector equation of YZ-Plane:

The YZ- Plane passes through origin whose position vector is $\vec{a}=\vec{0}$ 

and perpendicular to X-axis whose position vector is $\vec{i}$

So the equation of the YZ plane is $\vec{r}.\vec{n}=\vec{a}.\vec{n}$

⇒ $\vec{r}.\vec{i}=\vec{0}.\vec{i}$

$\vec{r}.\vec{i}=0$

Hence, the vector equation of the coordinates planes.

XY-Plane = $\vec{r}.\vec{k}=0$

XZ-Plane = $\vec{r}.\vec{j}=0$

YZ-Plane = $\vec{r}.\vec{i}=0$

问题4.找到以下每个平面的向量方程：

(i)2x – y + 2z = 8

解决方案：

Given equation of plane is,

2x – y + 2z = 8

So, 

$(x\hat{i}+y\hat{j}+z\hat{k})(2\hat{i}-\hat{j}+2\hat{k})=8$

$\vec{r}.(2\hat{i}-\hat{j}+2\hat{k})=8$

Therefore, the vector equation of the plane is $\vec{r}.(2\hat{i}-\hat{j}+2\hat{k})=8$

(ii)x + y – z = 5

解决方案：

Given equation of plane is,

x + y – z = 5

So, 

$(x\hat{i}+y\hat{j}+z\hat{k})(\hat{i}+\hat{j}-\hat{k})=5$

$\vec{r}.(\hat{i}+\hat{j}-\hat{k})=5$

Therefore, Vector equation of the plane is $\vec{r}.(\hat{i}+\hat{j}-\hat{k})=5$

(iii)x + y = 3

解决方案：

Given equation of plane is,

x + y = 3

So, 

$(x\hat{i}+y\hat{j}+z\hat{k})(\hat{i}+\hat{j})=3$

$\vec{r}.(\hat{i}+\hat{j})=3$

Therefore, the vector equation of the plane is $\vec{r}.(\hat{i}+\hat{j})=3$

问题5.找到通过点(1 、、-1、1)并垂直于连接点(1、2、5)和(-1、3、1)的线的平面的矢量和笛卡尔方程。

解决方案：

As we know that the vector equation of a plane passing through a point $\vec{a}$and normal to $\vec{n}$is

$(\vec{r}-\vec{a}).\vec{n} = 0$  …..(1)

So, according to the question it is given that the plane passes through the point (1, -1, 1) and 

normal to the line joining the points A(1, 2, 5) and B(-1, 3, 1).

So, 

$\vec{a}=\hat{i}-\hat{j}+\hat{k}$

$\vec{n}=\overrightarrow{AB}$

$\overrightarrow{AB}$= Position vector of $\vec{B}$ – Position vector of $\vec{A}$

= $(-\hat{i}+3\hat{j}+\hat{k})-(\hat{i}+2\hat{j}+5\hat{k})$

= $-2\hat{i}+\hat{j}-4\hat{k}$

Now, from eq (1), we get

$[\vec{r}-(\hat{i}-\hat{j}+\hat{k})].(-2\hat{i}+\hat{j}-4\hat{k})=0$

⇒ $\vec{r}.(-2\hat{i}+\hat{j}-4\hat{k})-(\hat{i}-\hat{j}+\hat{k}).(-2\hat{i}+\hat{j}-4\hat{k})=0$

⇒ $\vec{r}.(-2\hat{i}+\hat{j}-4\hat{k})-[-2-1-4]=0$

⇒ $\vec{r}.(-2\hat{i}+\hat{j}-4\hat{k})+7=0$

⇒ $\vec{r}.(-2\hat{i}+\hat{j}-4\hat{k})=-7$

⇒ $\vec{r}.(2\hat{i}-\hat{j}+4\hat{k})=7$  …(2)

Now, Putting $\vec{r}=x\hat{i}+y\hat{j}+j\hat{k}$ in eq(2), we get

$(x\hat{i}+y\hat{j}+j\hat{k}).(2\hat{i}-\hat{j}+4\hat{k})=7$

2x – y + 4z = 7

So, the vector equation is the plane is $\vec{r}.(2\hat{i}-\hat{j}+4\hat{k})=7$

and the cartesian equation of the plane is 2x – y + 4z = 7

问题6。 $\vec{n}$是幅度为√3的向量，并且与坐标轴成锐角均匀倾斜。求出通过(2，1，-1)且垂直于(2，1，-1)的平面方程的向量和笛卡尔形式$\vec{n}$

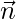
解决方案：

Given that $\vec{n}$ = √3 and $\vec{n}$ makes equal angle with coordinate axes.

Let us considered $\vec{n}$ has direction cosine as u, v and w, and

it makes angle of α, β and γ with the coordinate axes.

So, α = β = γ

cos α = cos β = cos γ 

Assuming u = v = w = p

We know that

u² + v² + w² = 1

p² + p² + p² = 1

P² = 1/3

P= ±1/√3 

So,

u = ±1/√3 

cos α = ±1/√3

Now, α = cos^-1(-1/√3) 

It gives, α is an obtuse angle so, neglect it.

Now, α = cos^-1(1/√3) 

It gives, α is an acute angle, so

cos α = ±1/√3

u = v = w = 1/√3

So, 

$\vec{n} = |\vec{n}|(l\vec{i}+m\vec{j}+n\vec{k})$

= √3$(\frac{1}{√3}\vec{i}+\frac{1}{√3}\vec{j}+\frac{1}{√3}\vec{k})$

Now, $\vec{n}=\hat{i}+\hat{j}+\hat{k}$and $\vec{a}=2\hat{i}+\hat{j}-\hat{k}$

As we know that the vector equation of a plane passing through a point $\vec{a}$ and normal to $\vec{n}$ is

$(\vec{r}-\vec{a}).\vec{n}=0$

$[\vec{r}-(2\hat{i}+\hat{j}-\hat{k})].(\hat{i}+\hat{j}+\hat{k})=0$

⇒ $\vec{r}(\hat{i}+\hat{j}+\hat{k})-(2\hat{i}+\hat{j}-\hat{k})(\hat{i}+\hat{j}+\hat{k})=0$

⇒ $\vec{r}(\hat{i}+\hat{j}+\hat{k})-(2+1-1)=0$

⇒ $\vec{r}(\hat{i}+\hat{j}+\hat{k})=2$  ….(1)

Now, Putting $\vec{r}=x\hat{i}+y\hat{j}+j\hat{k}$ in eq(1), we get

⇒ $(x\hat{i}+y\hat{j}+j\hat{k})(\hat{i}+\hat{j}+\hat{k})=2$

(x)(1) + (y)(1) + (z)(1) = 2

⇒ x + y + z = 2

Hence, the vector equation of the plane is $\vec{r}(\hat{i}+\hat{j}+\hat{k})=2$

and the cartesian equation of the plane is x + y + z = 2

问题7.从原点到平面的垂直线的脚坐标为(12，-4，3)。找到平面方程。

解决方案：

According to the question it is given that the coordinates of the foot of the 

perpendicular drawn from the origin O to a plane is P(12, -4, 3)

Thus, we can say that the required plane is passing through P(12, -4, 3) and perpendicular to OP.

As we know that the vector equation of a plane passing through a point $\vec{a}$ and normal to $\vec{n}$ is

$(\vec{r}-\vec{a}).\vec{n}=0$ …….(1)

Here, $\vec{a}=12\hat{i}-4\hat{j}+3\hat{k}$

$\vec{n}=(12\hat{i}-4\hat{j}+3\hat{k})-(0\hat{i}+0\hat{j}+0\hat{k})$

$\vec{n}=12\hat{i}-4\hat{j}+3\hat{k}$

On putting the values of $\vec{a}$ and $\vec{n}$ in equation (1)

$[\vec{r}-(12\hat{i}-4\hat{j}+3\hat{k})].(12\hat{i}-4\hat{j}+3\hat{k})=0$

⇒ $\vec{r}(12\hat{i}-4\hat{j}+3\hat{k})-(12\hat{i}-4\hat{j}+3\hat{k})(12\hat{i}-4\hat{j}+3\hat{k})=0$

⇒ $\vec{r}(12\hat{i}-4\hat{j}+3\hat{k})-[(12)(12)+(-4)(-4)+(3)(3)]=0$

⇒ $\vec{r}(12\hat{i}-4\hat{j}+3\hat{k})-(144+16+9)=0$

⇒ $\vec{r}(12\hat{i}-4\hat{j}+3\hat{k})=169$  ……..(2)

Now, on putting $\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$ in eq(2), we get

⇒ $(x\hat{i}+y\hat{j}+z\hat{k})(12\hat{i}-4\hat{j}+3\hat{k})-169=0$

(x)(12) + (y)(-4) + (z)(3) = 169

⇒ 12x – 4y + 3z = 169

Hence, the vector equation of the plane is $\vec{r}(12\hat{i}-4\hat{j}+3\hat{k})=169$

and the cartesian equation of the plane is 12x- 4y+ 3z = 169

问题8.考虑到垂直于平面的方向比例与(5，3，2)成比例，找到通过点(2，3，1)的平面方程。

解决方案：

According to the question it is given that the plane is passing through P(2, 3, 1) 

having (5, 3, 2) as the direction ratios of the normal to the plane.

As we know that the vector equation of a plane passing through a point $\vec{a}$ and normal to $\vec{n}$ is

$(\vec{r}-\vec{a}).\vec{n}=0$             …..(i)

So, $\vec{a}=2\hat{i}+3\hat{j}+\hat{k}$

$\vec{n}=5\hat{i}+3\hat{j}+2\hat{k}$

Now put all these values in equation (i),

$[\vec{r}-(2\hat{i}+3\hat{j}+\hat{k})].(5\hat{i}+3\hat{j}+2\hat{k})=0$

$\vec{r}(5\hat{i}+3\hat{j}+2\hat{k})-(2\hat{i}+3\hat{j}+\hat{k})(5\hat{i}+3\hat{j}+2\hat{k})=0$

$\vec{r}(5\hat{i}+3\hat{j}+2\hat{k})-[(2)(5)+(3)(3)+(1)(2)]=0$

$\vec{r}(5\hat{i}+3\hat{j}+2\hat{k})-[10+9+2]=0$

$\vec{r}(5\hat{i}+3\hat{j}+2\hat{k})-21=0$  ………(2)

Now, putting, $\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$ in eq(2), we get

$(x\hat{i}+y\hat{j}+z\hat{k})(5\hat{i}+3\hat{j}+2\hat{k})-21=0$

(x)(5) + (y)(3) + (z)(2) = 21

5x + 3y + 2z = 21

Hence, this is the required equation of plane

问题9.如果轴垂直且P是点(2，3，-1)，则找到与P成直角的P平面的方程。

解决方案：

According to the question it is given that P is the point (2,3,-1) and 

the plane is passing through P and OP is the vector normal to the plane.

So, 

As we know that the vector equation of a plane passing through a point $\vec{a}$ and normal to $\vec{n}$ is

$(\vec{r}-\vec{a}).\vec{n}=0$              …..(i)

Here, $\vec{a}=2\hat{i}+3\hat{j}-\hat{k}$

$\vec{n}=\overrightarrow{OP}$

So, $\overrightarrow{OP}$ = Position vector of P – Position vector of O

= $(2\hat{i}+3\hat{j}-\hat{k})-(0\hat{i}+0\hat{j}+0\hat{k})$

$\vec{n}=(2\hat{i}+3\hat{j}-\hat{k})$

Now put, the value of $\vec{a}$ and $\vec{n}$ in equation (i),

$[\vec{r}-(2\hat{i}+3\hat{j}-\hat{k})].(2\hat{i}+3\hat{j}-\hat{k})=0$

$\vec{r}(2\hat{i}+3\hat{j}-\hat{k})-[2\hat{i}+3\hat{j}-\hat{k})(2\hat{i}+3\hat{j}-\hat{k})]=0$

$\vec{r}(2\hat{i}+3\hat{j}-\hat{k})-[(2)(2)+(3)(3)+(-1)(-1)]=0$

$\vec{r}(2\hat{i}+3\hat{j}-\hat{k})-[4+9+1]=0$

$\vec{r}(2\hat{i}+3\hat{j}-\hat{k})=14$   ……..(2)

Now putting, $\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$, in eq(2), we get

$(x\hat{i}+y\hat{j}+z\hat{k})(2\hat{i}+3\hat{j}-\hat{k})=14$

(x)(2) + (y)(3) + (z)(−1) = 14

2x + 3y − z = 14

So, this is the required equation of plane.

问题10：找到平面2x + y -2z = 3在坐标轴上产生的截距，并找到平面法线的方向余弦。

解决方案：

According to the question

The equation os plane = 2x + y -2z = 3

Now divide both sides of the equation by 3, we get

$\frac{2x}{3}+\frac{y}{3}-\frac{2z}{3}=\frac{3}{3}$

$\frac{x}{3/2}{}+\frac{y}{3}+\frac{z}{-3/2}=1$        ……(i)

Here, if a, b, c are the intercepts by a plane on the coordinates axes,

then the equation of the plane is:

$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$                     ……(ii)

On comparing the equation (i) and (ii), we get the value of a, b, and c

$a=\frac{3}{2}, b=\frac{3}{1}, c=-\frac{3}{2}$

So, from the given equation of plane,

$(x\hat{i}+y\hat{j}+z\hat{k})(2\hat{i}+\hat{j}-2\hat{k})=3$

$\vec{r}(2\hat{i}+\hat{j}-2\hat{k})=3$

Hence, the vector normal to the plane is,

$\vec{n}=2\hat{i}+\hat{j}-2\hat{k}$

$|\vec{n}|$ = √{(2)² + (1)² + (-2)²}

= √(4 + 1 + 4)

= √9

$|\vec{n}|=3$

Hence, the unit vector perpendicular to $\vec{n}= \frac{\vec{n}}{|\vec{n}|}= \frac{2\vec{i} + \vec{j}-2\vec{k}}{3}$

Hence, the direction cosine of normal to the plane = 2/3, 1/3, -2/3